柔性作业车间调度优化的改进遗传退火算法

（兰州交通大学 交通运输学院，兰州 730070）

0 引言

制造业是国民经济的主体，是立国之本、兴国之器、强国之基。随着《中国制造2025》的提出以及为了加快实现到2025年我国迈入制造强国的战略目标，制造行业对于车间的调度方案优化、效率优化等研究有着迫切的需求。

车间调度问题（Job-shop Scheduling Problem，JSP）是制造业研究的核心和重点。其中柔性作业车间调度（Flexible Job-shop Scheduling Problem，FJSP）是JSP问题的延伸和拓展，FJSP突破了资源唯一性的限制，每道工序可以在多台不同的机器上加工，这样，FJSP便衍生了两个子问题，即机器分配问题和工序调度问题，从而使得其相对于经典JSP而言更加复杂，但同时又使其更加符合实际的生产环境，因此对它的研究更加具有理论价值和实际应用价值。

FJSP是一类满足任务配置和顺序约束要求的组合优化问题，属于NP难问题[1]。近年来，学者们相继提出了一系列启发式算法和智能算法，取得了一些成果。如：Brandimarte[2]采用分层的思想，他先采用现有的分派规则解决路径子问题，然后再利用禁忌搜索算法解决排序子问题[3]；Xia和Wu[4]运用粒子群算法与模拟退火算法混合求解多目标FJSP问题；Gao J[5,6]将遗传算法与局部搜索相结合，并改进了交叉变异算子，提出新的遗传算法；Pezzella[7]通过集成不同的遗传策略来产生初始种群，设计了求解FJSP问题性能更好的遗传算法。国内研究FJSP的文献也很多；赵良辉[8]、潘全科[9]采用模拟退火算法求解车间调度问题；吴秀丽[10～12]相继提出了小生境技术的混合遗传算法、免疫遗传算法、改进的细菌觅食优化算法求解FJSP问题；张超勇[13～15]在提出POX交叉算子的前提下，之后又将其改进提出了改进的遗传算法和改进的非支配排序遗传算法（NSGA-II）求解FJSP问题；徐新黎[16]、李小涛[17]分别多智能题免疫算法和多智能体遗传算法求解车间调度问题；刘爱军[18]、蒋增强[19]分别提出了基于血缘变异和改进的NSGA-II求解多目标柔性作业车间调度问题。由此可知，柔性作业车间调度问题是当前学术界和工业界关注的热点问题。

基于此背景及混合算法能提高单一算法性能的思想，本文在前人研究的基础上[20～23]，提出了改进的遗传退火算法（Enhanced Genetic and Simulated Annealing,EGSA），引入了S-自适应遗传算子以及采用非齐次的降温策略[24,25]，不仅能对交叉和变异概率进行非线性调整而且还能很好的控制温度的下降，增强了遗传算法良好的全局搜索能力和模拟退火算法有效避免陷入局部最优的能力。

1 问题模型

1.1 问题的描述

1）每一工序必须一次加工完成，不允许中途中断（非抢占式调度）；

2）一台机器在任何时刻最多只能加工一个产品；

3）一个产品不能同时在两台机器上加工；

4）在t=0时刻，所有的工件都可被加工。

1.2 模型的建立

FJSP的调度目标是找出n个工件所有工序的加工顺序，并分配相应的机器，使其最大完工时间最小。设T为调度方案的最大完工时间Makespan，Cij为工序Oij的完工时间，则数学模型为：

其中：1）是目标函数；2）反映的是工艺约束；3）限定一台机器同一时间只能加工一个工件；4）限定工序Oij只能在一台机器上独立完成，不能跨机器加工；5）和 6）是决策变量。

2 改进遗传退火算法的FJSP寻优

2.1 编码和解码

利用遗传算法对非确定多项式难题（NP）进行优化的关键之一就是编码。FJSP是要解决机器上工件工序的排序问题及机器的分配问题，因此只采用单一的基于工序的编码、基于工件的编码、基于析取图的编码、基于机器的编码等[26]难以得到问题的最优解。所以本文采用基于工序编码和基于机器编码的双层编码方式，如图2所示，此编码将工序和机器对应起来不仅能保证产生可行调度而且还可以避免死锁。

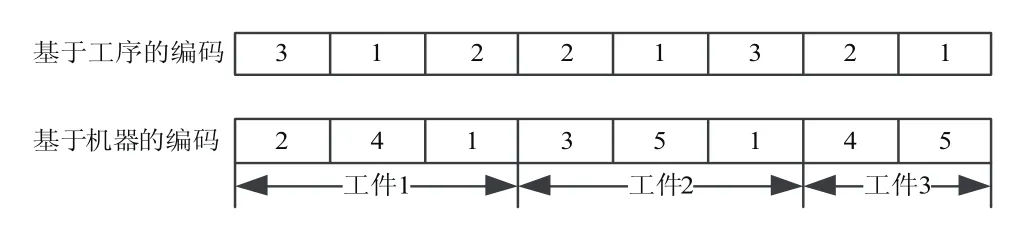
图1 基于工序和机器的双层编码

图1的染色体表示有3个工件共8个工序，在5个设备上进行加工。其中基于工序的编码出现的第一个3表示工件3的第1道工序，即O31，再对应基于机器的编码工件3的部分，则O31对应机器4，即：同理可得：。解码时根据解的前半段工序编码和后半段工序所对应的机器机器编码依次计算工序的开始和完工时间即可。

2.2 交叉和变异

2.2.1 自适应交叉变异算子

在一般的遗传算法中，交叉概率pC和变异概率pM采用给定的固定值，这将有可能导致在求解较复杂问题时，当种群的适应度趋于局部最优时，固定的pC和pM难以使算法及时跳出局部最优；而对于适应度高于种群平均适应度的个体，固定的pC和pM又难以保护个体的优良基因。因此采用固定的pC和pM在求解复杂优化问题时算法存在早熟及稳定性差等缺点。于是，为了提高算法搜索全局最优解的能力，中外学者如：Srinvas[27]、王小平[28]、石山[29]、王万良[30]等人对自适应遗传算子进行了研究，并取得了很好的成果。因此本文引入了能对交叉和变异概率进行非线性调整得S-自适应交叉变异算子，其表达式如下：

其中：fmax为种群中最大的适应度值，favg为每代种群的平均适应度值，f′表示交叉的两个个体中较大的适应度值，f是被选择变异个体的适应度值；一般地，k1=k2=1，k3=k4=0.5，c=0.6。

该方法所构造的遗传算子随种群适应度变化而自适应调整交叉变异概率。能对偏离最优解的个体自动采用较大的pC和pM，以产生向最优解方向移动的新个体，提高搜索速度；对靠近最优解的个体自动采用较小的pC和pM，保护个体的优良基因，使个体逐渐接近全局最优解。

2.2.2 交叉操作

在JSP问题中，常用的交叉策略有JOX、SXX、PPX、SPX、GT、LOX等[31]，研究表明设计交叉算子最重要的标准是子代对父代优良特征的继承性和子代的可行性。

1）工序的IPOX交叉策略

IPOX交叉策略仅交叉父代工序的加工顺序，保留工件中工序分配的机器到子代。设有父代1和父代2，通过IPOX交叉后产生的子代1和子代2，其交叉步骤如下：

Step1：将工件分成两个集合JS1和JS2；假定分组结果为JS1={1,3}，JS2={2}；

Step2：将父代1/父代2中包含在JS1/JS2的工件复制到子代1/子代2中，同时不改变基因的位置；

Step3：将父代1/父代2中包含在JS1/JS2的工件复制到子代2/子代1，同时不改变它们的次序，以下是图解说明。

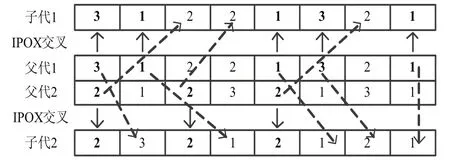
图2 工序的IPOX交叉策略

2）机器的交替位置交叉策略

APX是轮流选择父代1和父代2中的基因，若某一基因在子代出现的次数超过了在父代出现的次数，则后续不再选择该基因，按以上规则，直到子代的长度达到父代染色体的长度为止。具体操作如图3所示。

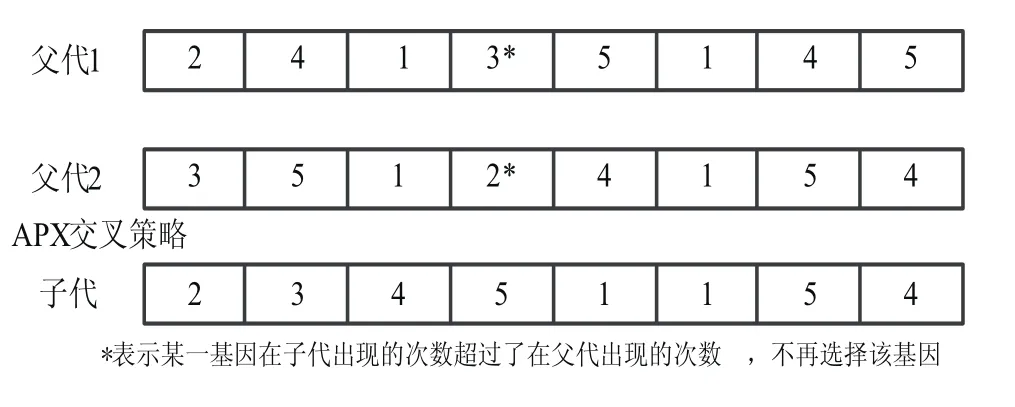
图3 机器的APX交叉策略

2.2.3 变异操作

1）工序的改进倒位变异策略

本文改进的倒位变异策略EIVM，其具体操作如下：设父代染色体的长度为L，则从父代的随机位置选取长度不超过所选位置到L区间的子基因串，然后将这个基因串中所有的子基因倒位后再随机的插入染色体中，得到新的子代。

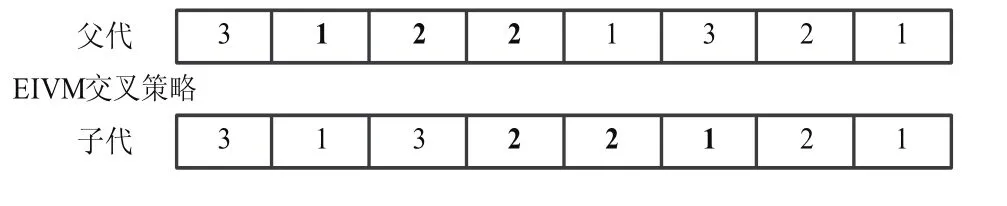
图4 工序的EIVM变异策略

2）机器编码的随机替换变异策略

由于柔性JSP中每道工序可以有多台机器进行加工的特点，因此，在机器染色体变异时，在基因串中随机选择一个基因，在此基因的机器集合中随机选择一个与它不相等的整数（不同的机器），替换当前的基因，这样可保证的解是可行解。

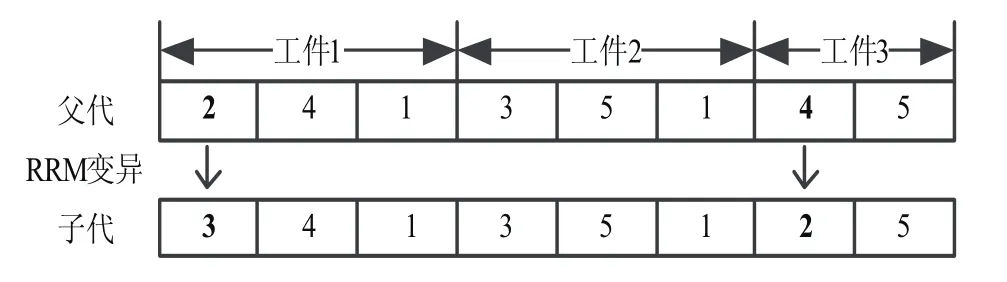
图5 机器的RRM变异策略

2.3 降温规则

利用模拟退火算法对每个染色体开展局部搜索时，精细的冷却退火规则能够使算法在有限次的迭代过程中逼近问题的最优解。本文的温度下降指定一个有限的非齐次马尔可夫链序列，温度更新表达式为：

2.4 停止规则

在整个搜索算法过程中，有两个终止规则。第一个是给定的最大的迭代次数M，另外一个是降温达到终止温度tf（即当满足以上要求之一时，终止运算。

2.5 算法步骤

Step1：初始化，给定种群规模MAXPOP，k=0；初始温度种群pop(k)；

Step2：如果满足停止规则，停止计算；否则，对种群pop(k)中每一个染色体i∈ p op(k)的邻域中随机选状态按模拟退火中的接受概率：

接受或拒绝j，其中f(i)为状态i的目标值；这一阶段共需MAXPOP次迭代选出新种群NewPOP1（k+1）；

Step3：在NewPOP1（k+1）中计算适应函数：

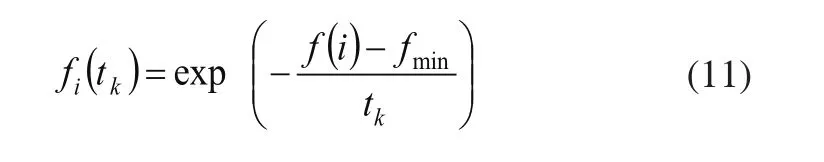
其中fmin是NewPOP1（k+1）中的最小值；由适应函数决定的概率分布从NewPOP1（k+1）中随机选MAXPOP个染色体形成种群NewPOP2（k+1）；

Step4：按遗传算法的S-自适应算子进行IPOX、APX交叉得到CrossPOP（k+1）；再通过EIVM、RRM变异得到MutPOP（k+1）；

3 仿真实验

本算法使用仿真工具为：Matlab R2016b；运行环境：Windows 7；处理器：Intel(R) Core(TM) i5-2450M CPU @2.50GHz 4.0GB内存。

参数设置如下：种群规模为200，c=0.6，初始温度t0=100，终止温度tf=10，温度可以下降的最大次数M=1000。

为了验证EGSA算法的有效性和可行性，本文选取柔性作业车间调度Kacem的3个基准问题（8×8、10×10、15×10）进行求解[32]，并与当前取得效果比较好的算法进行比较，如：PSO+SA[4]、PSO+TS[33]、LSA[34]等。对这三个基准问题应用本文提出的EGSA分别运行10次，得到的统计结果如表1所示。

由表可知本文的EGSA算法在求解这三个算例时，都能在很短的时间得到最优解，并且在8×8、15×10的算例上，表现出更明显的优势，分别比其他4种、2种算法得到的解更优，说明ESGA算法具有高效性和精确性的特点。

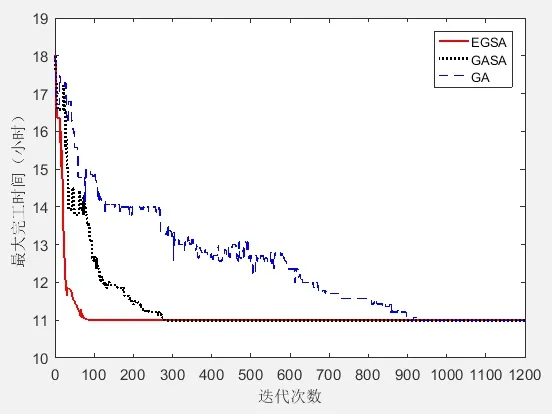
图6 三种算法求解Kacem 15×10算例的收敛曲线对比图

为了说明算法的性能，本文将15×10的基准问题为算例，将本文提出的EGSA同时算法与传统的遗传退火算法GASA、遗传算法GA进行收敛性能对比，三种算法的收敛曲线图如图6所示。由收敛图可知三种算法都能寻找到最优解11小时；EGSA在第76代就开始收敛到最优解，GASA大约在第300代开始收敛到最优解；而GA收敛速度最慢，迭代到第900代左右才收敛到最优，且根据其目标值在约100代到600代的变化情况，可知其鲁棒性稍差。通过对比发现，混合算法（EGSA、GASA）比单一算法（GA）性能更优，鲁棒性更好，同时也说明了EGSA算法不仅高效、精度高而且收敛速度快，具有较强的搜索能力，能够在较短时间与迭代次数内获取最优解。

表1 EGSA求解Kacem算例结果统计与对比

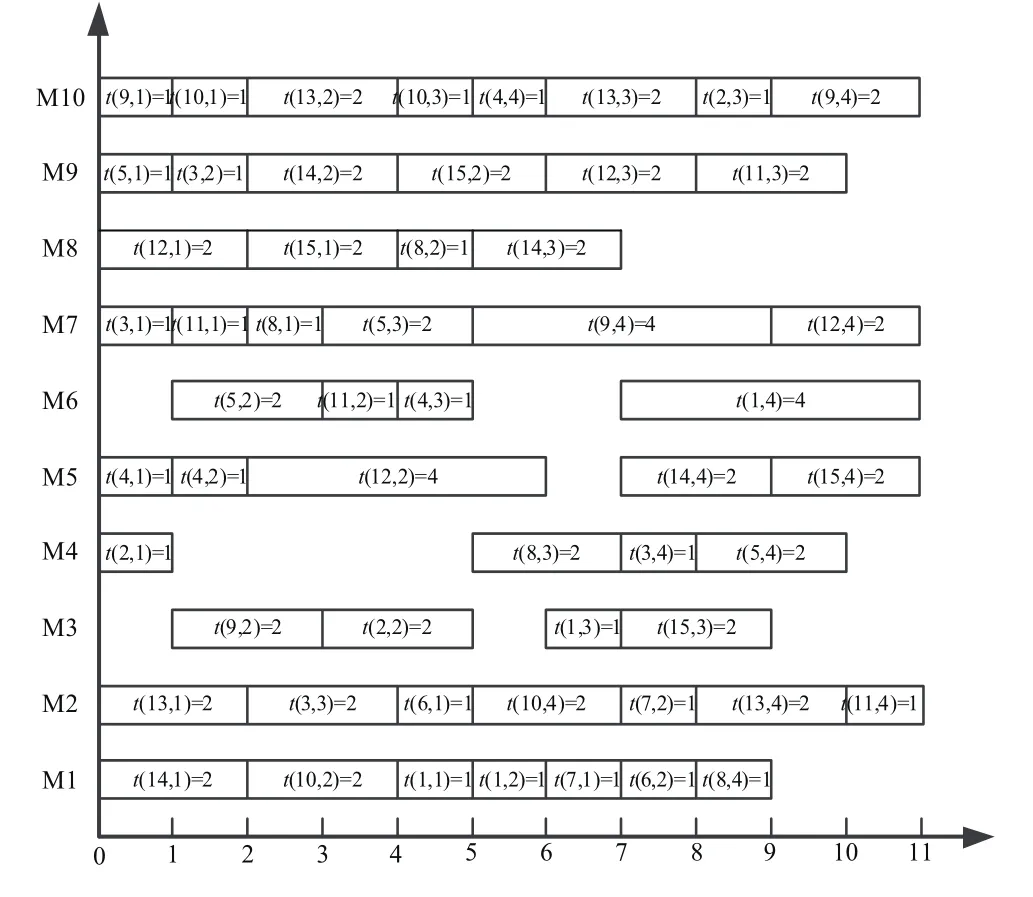
图7 Kacem15×10最优调度方案

由上述收敛曲线对比得出的Kacem15×10最优调度方案的甘特图如图7所示。由图可知机器M2、M7、M10从t=0时刻开始直到任务结束，一直处于工作状态。若定义：机器负荷=工作时间/最大完工时间，则这三台机器的工作负荷均为100%，表明这三台机器工作强度很高，所以企业应该加强对这几台机器的日常保养和维护工作。

4 结论

柔性作业车间调度是实施生产计划的重要环节，本文建立了以最小化最大完工时间为优化目标的FJSP模型，提出了一种改进的遗传退火算法。为了克服传统算法采用的固定交叉变异概率和固定温度衰减系数带来的易早熟、稳定性差等缺点，于是引进了S-自适应算子和非齐次的降温规则对算法进行改进。最后使用MATLAB工具将算法对Kacem基准算例进行了测试，也与传统算法进行了收敛性对比，结果表明本文提出的算法具有较好的可行性、高效性、精确性、鲁棒性，并提出企业在实际管理中应该注意的问题。

由于作者水平有限，只是研究了单目标的FJSP问题，并没有研究多目标的FJSP问题，在实际中生产中，制造商不仅要考虑最大完工时间，而且还需要考虑设备负荷、加工成本、能耗、客户满意度等综合因素，因此多目标的FJSP问题将是下一步研究的重点内容。