高校、监考教师、大学生三方考试博弈关系研究
2019-01-18余利娥
余利娥
(宿州学院商学院,安徽宿州234000)
近年来,大学生考试作弊已经成为一种普遍现象,很多监考教师对大学生的作弊行为也是睁一只眼闭一只眼。大学生的考试作弊行为严重影响了高校是优秀人才培养基地的良好形象。首先,大学生考试作弊影响高校考风建设;其次,作弊的大学生平时不努力学习,考试时通过作弊获得高分,会引起不作弊学生的不公平感,会导致越来越多的大学生不刻苦学习,影响高校学风的建设;最后,大学生通过作弊的方式获得高分,考试成绩无法反映出学生掌握专业知识的真实情况,不利于授课教师改进教学方法,影响高校教学质量的提高。因此,对于各高校来说,防止大学生考试作弊是高校考风、学风、教风建设的重点。
为了防止大学生考试作弊,组织监考教师监考是高校常见的手段。关于监考教师和大学生考试作弊行为关系的研究文献较多。曹菊琴和许红平认为监考教师的责任心对大学生的考试作弊行为有重要影响。[1-2]张长温和陈绍刚分别构建了完全信息和非完全信息的“监考博弈”模型,分析了大学生考试作弊的动机、后果与对策。[3]张琼通过构建学校和学生之间的监考博弈模型,发现仅通过监考制度无法解决学生的作弊问题,还需要强调诚信建设。[4]宋结焱通过对监考博弈的重新审视,研究了监考博弈中纯策略纳什均衡的变异问题,并提出了三项修正措施。[5]何计蓉、高辉和花海燕从经济学博弈论的视角出发对监考教师和大学生进行了收益—成本分析,发现监考教师的考场严厉程度、大学生的专业偏好会影响大学生的作弊行为。[6]冯银虎、董杰和马田媛通过构建监考教师与学生之间的博弈模型,发现只有提高对监考教师的关注度,加大监考力度才能有效地防止大学生作弊。[7]刘继伟通过构建监考者和大学生之间的监督博弈模型,解释了大学生作弊的内在原因。[8]李元丽基于风险博彩理论,分析了监考教师监考力度和处罚力度对大学生作弊行为的影响。[9]从目前的相关研究文献来看,学者们主要集中于研究监考教师和大学生两方之间的考试博弈问题,而忽略了高校这一主体的参与,实际上,高校通过加强巡考来督促监考教师严格监考,防止大学生考试作弊。监考教师是否会严格监考、大学生是否选择作弊将会受到高校巡考决策的影响。同时,监考教师是否会严格监考,大学生是否选择作弊也会影响高校的巡考决策。在防止大学生考试作弊的过程中,高校、监考教师和大学生会同时参与,防止大学生考试作弊的成效取决于三方利益博弈的结果。同时,三方博弈理论已经在很多领域得到广泛应用。[10-12]因此,只有三方博弈的结果才能决定防止大学生作弊的成效。而且,三方博弈理论也已经比较成熟。[10-12]基于此,本文在考虑高校、监考教师与大学生三者之间关系的基础上,建立三方共同参与的博弈模型,并通过求解博弈模型的混合纳什均衡,找出影响均衡的关键因素,给出高校防止大学生考试作弊的建议,以提高高校防止大学生考试作弊的效率。
一、问题描述及假设说明
本文以高校、监考教师和大学生组成的考试系统作为研究对象。博弈的参与主体包含高校、监考教师和学生。假设高校、监考教师和学生都是理性人,均以自身利益最大化为目标。高校的策略集合为:巡考和不巡考;监考教师的策略集合为:严格监考和不严格监考;学生的策略集合为:作弊和不作弊。当高校巡考时,如若抓住学生作弊,对作弊学生进行严惩,表明高校狠抓考风考纪的决心,有利于树立高校严谨务实的良好形象,有利于吸引优秀高中毕业生报考,而且也有助于提高高校毕业生的质量,因此假设高校选择巡考,且学生选择作弊时,高校能获得Vu的收益。不失一般性,假设当高校不巡考,或高校巡考,而学生不作弊时,高校的收益为0。由于高校组织巡考,需要付出一定的成本(例如:巡考工作组的巡考费、巡考相关材料的准备等),因此,本文假设高校巡考的成本为Cu。假设高校对监考教师实施奖惩制度,即当高校巡考,且学生作弊时,如果监考教师选择严格监考,抓住作弊的学生,高校将会给予监考教师一定的奖励,假设该奖励为Vt;而当高校巡考,且学生作弊时,如果监考教师选择不严格监考,高校抓住了作弊的学生,将会给予监考教师一定的惩罚,假设该惩罚为Ft。当监考教师选择严格监考时,需要付出一定的劳动,因此,不失一般性,假设监考教师不严格监考的成本为0,严格监考的成本为Ct。不失一般性,假设学生考试不作弊的正常收益为0,考试作弊的投机收益为Vs。学生作弊需要付出一定的成本(购买作弊工具、准备作弊材料等),假设此成本为Cs,因此,学生考试作弊的净收益为Vs-Cs。作为理性人,只有当Vs-Cs>0时,学生才会选择作弊,因此,本文假设Vs-Cs>0。假设当高校或监考教师抓住学生作弊时,对作弊学生的惩罚均为Fs(包括成绩记为0、通报批评等)。假设高校巡考的概率为P1(0 本文分别构建高校与监考教师之间、高校与学生之间、监考教师与学生之间的两两参与混合策略博弈模型。 表1 高校与监考教师之间的收益矩阵 由表1中监考教师的收益结果可知,当Vt-Ct<-Ft,即Vt+Ft-Ct<0时,无论高校是否巡考,监考教师都会选择不严格监考,为了督促监考教师严格监考,本文假设高校给予监考教师严格监考的奖励和不严格监考的惩罚满足Vt+Ft-Ct>0。 表2 高校与学生之间的收益矩阵 由表3中学生的收益结果可知,当Vs-Cs-Fs>0时,无论高校是否巡考,学生都会选择作弊,高校的巡考工作没有意义,因此,为了防止学生考试作弊,本文假设高校对作弊学生的惩罚满足Vs-Cs-Fs<0。 表3 监考教师与学生之间的收益矩阵 在高校防止大学生考试作弊的工作中,高校、监考教师和大学生实际上会同时参与,为了提高高校防止大学生考试作弊的效率,寻求提高监考教师严格监考的概率和降低大学生考试作弊的概率的有效途径,需要构建高校、监考教师和大学生三方参与的博弈模型。 根据高校、监考教师和学生的策略集合可以得出三方同时参与的博弈模型的策略组合有八种:(巡考,严格监考,作弊);(巡考,严格监考,不作弊);(巡考,不严格监考,作弊);(巡考,不严格监考,不作弊);(不巡考,严格监考,作弊);(不巡考,严格监考,不作弊);(不巡考,不严格监考,作弊);(不巡考,不严格监考,不作弊)。根据模型假设确定各参与主体的收益矩阵,如表4所示,表中的博弈策略和收益结果分别对应高校、监考教师和学生。 表4 高校、监考教师和学生三方博弈收益矩阵 由表4中监考教师的收益结果可知,当学生选择不作弊时,监考教师选择不严格监考总能获得更大的收益,因此,高校、监考教师和学生之间不存在(巡考,严格监考,不作弊)和(不巡考,严格监考,不作弊)的策略组合。同时,由表4中高校的收益结果可知,当监考教师选择不严格监考,且学生选择不作弊时,高校选择不巡考总能获得更大的收益,因此,高校、监考教师和学生之间也不存在(巡考,不严格监考,不作弊)的策略组合。因此,高校、监考教师和学生三方同时参与的博弈模型的策略组合实际上只有五种:(巡考,严格监考,作弊);(巡考,不严格监考,作弊);(不巡考,严格监考,作弊);(不巡考,不严格监考,作弊);(不巡考,不严格监考,不作弊)。相应的各参与主体的收益矩阵如表5所示。 表5 高校、监考教师和学生三方博弈实际收益矩阵 (1)根据构建的高校、监考教师和学生三方博弈模型实际收益矩阵,在高校巡考概率P1和学生作弊概率P3给定的情况下,监考教师严格监考的期望收益为: E(严格监考)=P1P3(Vt-Ct)+(1-P1)P3(Vt-Ct)=P3(Vt-Ct) (1) 监考教师不严格监考的期望收益为: E(不严格监考)=P1P3(-Ft)+(1-P1)P3×0+(1-P1)(1-P3)×0=P1P3(-Ft) (2) 当监考教师严格监考和不严格监考的收益函数相等时,实现博弈均衡,即 E(严格监考)=E(不严格监考) P3(Vt-Ct)=P1P3(-Ft) (3) (2)给定监考教师严格监考的概率P2和学生作弊的概率P3,高校巡考的期望收益为: E(巡考)=P2P3(Vu-Cu-Vt)+(1-P2)P3(Vu-Cu+Ft)=P3(Vu-Cu)-P2P3(Vt+Ft)+P3Ft (4) 高校不巡考的期望收益为: E(不巡考)=P2P3(-Vt)+(1-P2)P3×0+(1-P2)(1-P3)×0=-P2P3Vt 当高校巡考和不巡考的收益函数相等时,实现博弈均衡,即 E(巡考)=E(不巡考) P3(Vu-Cu)-P2P3(Vt+Ft)+P3Ft=-P2P3Vt (5) (3)给定高校巡考的概率P1和监考教师严格监考的概率P2,学生考试作弊的期望收益为: E(作弊)=P1P2(Vs-Cs-Fs)+P1(1-P2)(Vs-Cs-Fs)+(1-P1)P2(Vs-Cs-Fs)+ (1-P1)(1-P2)(Vs-Cs)=Vs-Cs-(P1+P2-P1P2)Fs (6) E(不作弊)=(1-P1)(1-P2)×0=0 (7) 将P1*和P2*代入式(6),可以得到: (8) 因此,当E(作弊)>E(不作弊),即Ft2(Vs-Cs-Fs)-(Vu-Cu)(Ft+Vt-Ct)>0时,学生会选择作弊,因为此时学生作弊的期望收益大于不作弊的期望收益。当Ft2(Vs-Cs-Fs)-(Vu-Cu)(Ft+Vt-Ct)<0时,学生会选择不作弊,因为此时学生不作弊的期望收益大于作弊的期望收益。 为了防止大学生考试作弊、督促监考教师严格监考,提高高校巡考的效率,接下来本文重点分析各参数对博弈模型混合策略纳什均衡的影响。 1.影响高校巡考的因素 命题1 高校巡考的纳什均衡解P2*的大小与Ct、Vt、Ft三个因素有关,且与Ct成正比,与Vt、Ft成反比。 命题1表明高校巡考的概率主要和监考教师严格监考付出的成本、高校给予监考教师严格监考的奖励力度和不严格监考的惩罚力度有关。降低监考教师严格监考的成本,提高高校给予监考教师严格监考的奖励力度,有利于提高对监考教师严格监考的刺激力度,鼓励监考教师严格监考,从而降低高校巡考的概率,提高高校巡考的效率。同时,提高高校对监考教师不严格监考的惩罚力度,可以对监考教师起到较大的威慑作用,监考教师不敢轻易选择不严格监考,能有效提高监考教师严格监考的概率,提高高校巡考的效率。 2.影响监考教师严格监考的因素 命题2 监考教师严格监考的纳什均衡解P2*的大小与Ft、Vu、Cu三个因素有关,且与Ft、Vu成正比,与Cu成反比。 命题2表明监考教师严格监考的概率主要和高校对监考教师不严格监考的惩罚力度、高校巡考的收益以及成本有关。高校提高对监考教师不严格监考的惩罚力度,可以对监考教师起到较大的威慑作用,监考教师会提高严格监考的概率。同时,增加高校巡考的收益、降低高校巡考的成本,能有效提高监考教师严格监考的概率。 3.各参数对大学生作弊行为的影响 命题3 大学生的作弊行为受到大学生作弊的投机收益、成本、受到的惩罚力度、监考教师严格监考获得的奖励、付出的成本、不严格监考得到的惩罚以及高校巡考的收益和成本的影响,且当大学生作弊的投机收益较小,作弊的成本、受到的惩罚力度较大,监考教师严格监考获得的奖励较小、付出的成本较大,高校巡考的收益较大、成本较小时,学生更易于选择不作弊。 证明 由于当Ft2(Vs-Cs-Fs)-(Vu-Cu)(Ft+Vt-Ct)<0,即 (Cu-Vu)(Ft+Vt-Ct) 防止大学生考试作弊对高校考风、学风、教风建设意义重大,高校是防止大学生考试作弊的关键。根据高校、监考教师和学生的三方博弈模型的研究结果可知,监考教师严格监考的概率、大学生作弊的行为选择与大学生作弊的投机收益、成本、受到的惩罚力度、监考教师严格监考获得的奖励、付出的成本、不严格监考得到的惩罚以及高校巡考的收益和成本相关。因此,从高校角度,提高监考教师严格监考的概率,防止大学生考试作弊,提高高校巡考效率的主要措施有: 提高对监考教师不严格监考的惩罚力度。对监考教师不严格监考的惩罚,应该包括经济惩罚和行政惩罚。通过经济惩罚虽然可以抵消部分高校巡考的成本,又可以对监考教师的不严格监考行为起到威慑作用,但是,对于监考教师而言,经济惩罚的威慑作用有限,行政惩罚的威慑力更大。高校应该提高对监考教师不严格监考的行政惩罚力度,例如:监考教师不严格监考将影响职称的评定,使监考教师不敢心存侥幸。 提高对学生作弊行为的惩罚力度。目前很多高校对学生作弊行为的态度是“高高拿起,轻轻落下”,学生手册中对学生各种作弊行为的处罚规定很严格,但是在实际应用上却是一轻再轻。很多学生作弊,监考教师只是将其赶出考场,没有做任何的处理,学生作弊被抓后,如果考试成绩不及格,还能参加下一学期期初的课程补考,考试作弊对于学生而言没有任何的风险。因此,高校只有严格执行对作弊学生的惩罚规定,提高对学生作弊行为的惩罚力度,才能对学生的作弊行为起到威慑作用,防止学生考试作弊。 降低高校巡考的成本。高校可以利用各种信息技术来降低巡考的成本,例如在教室安装摄像头。虽然短期来看,安装摄像头一次性资金投入较大,但是从长期来看,其成本远低于组织巡考组对一间间教室进行巡考。同时,高校可以在考场统一安装电子信号屏蔽仪,一方面可以防止学生利用电子设备作弊,另一方面也可以有效避免监考教师在监考时玩手机,提高监考的有效性,降低巡考的难度,从而降低巡考工作组付出的成本。二、高校、监考教师和大学生两两参与的博弈模型构建
(一)高校与监考教师之间的博弈模型


(二)高校与学生之间的博弈模型

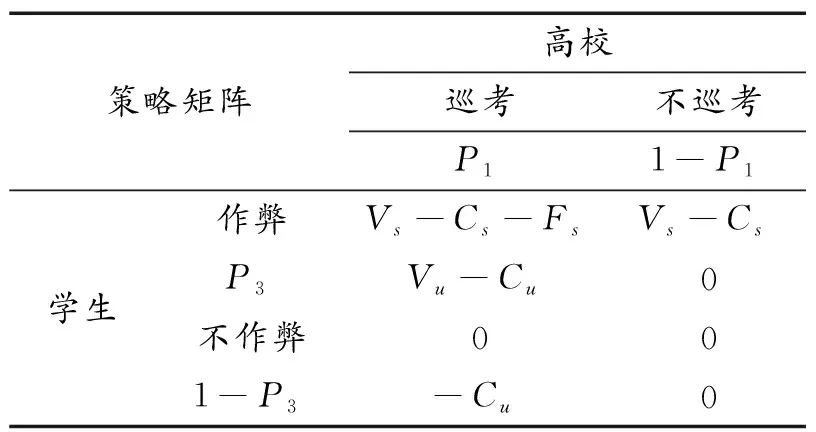
(三)监考教师与学生之间的博弈模型


三、高校、监考教师和大学生三方参与的博弈模型分析
(一)三方参与博弈模型的策略组合

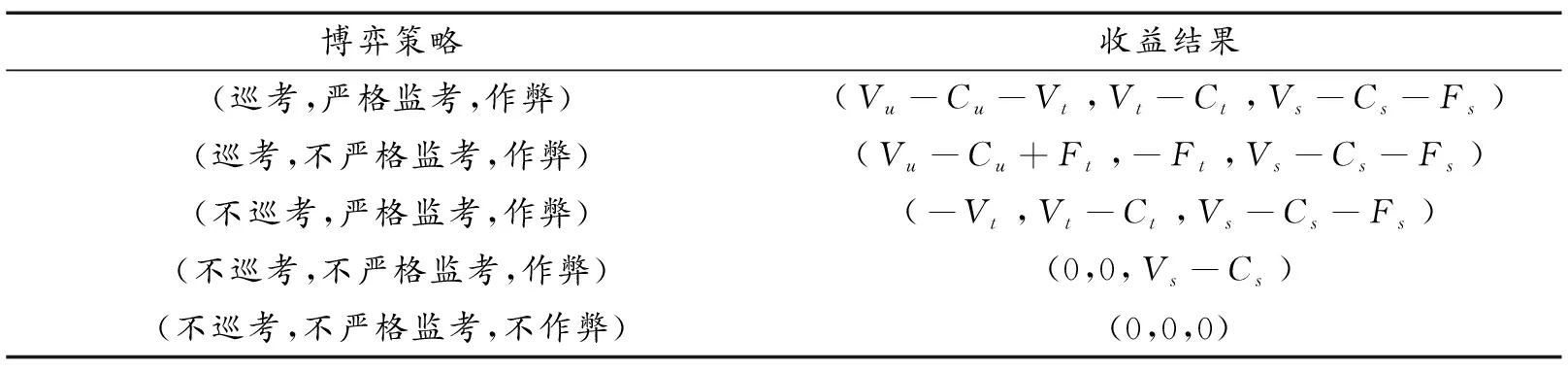
(二)模型求解



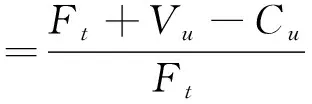

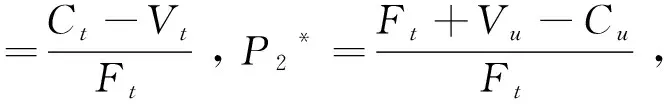
(三)结果分析
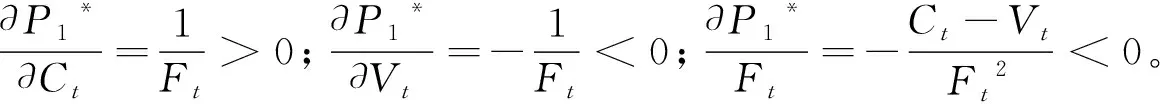

四、结论与建议
