风机弹簧减震器的效率计算*

曹 静，谭浩华，荣光伟

(1.英格索兰亚太技术工程中心，上海 200051； 2.英格索兰亚太技术工程中心，江苏 太仓 215400 )

0 引 言

新项目是新一代屋顶机产品的设计，其主要零部件之一室内风机是重新选型的，新选择的后倾式离心风机具有风量大、压力低但效率高的特点，在暖通行业应用十分广泛。新的风机选定之后相应的配件要重新选择，支撑结构也要重新设计，测试等工作任务艰巨。如果测试过程中发现风机有问题还需要修改重来，很是费时；如果在前期能准确选择某些零部件并确保他们的可靠性，那测试时出现问题的概率会小并能及时排除某些确定的因素找到问题的根本原因。弹簧减震器是风机结构中不可缺少的一部分,它具有性能稳定、承载能力强、寿命长、抗环境污染能力强、计算可靠和固有频率低等优点。笔者结合Creo软件,通过这一简单快速的计算方法来校核弹簧减震器的选型是否合理，使其达到期望的减震效果，在实践中有重要的意义。

1 理论分析

在许多工程问题中，我们并不希望产生机械振动，而在诸如搅拌机、振动器等系统中，却又希望产生振动。由于振动系统是具有一定质量且其中部件能相对运动的系统，因此具有弹性构件可以储存弹性能，系统的阻尼可以把部分能量转化为热能以及通过基座激励可使能量转化为系统的能量。本文着重分析系统阻尼和基座激励对风机弹簧减震器的影响。

1.1 小阻尼对振动系统的影响

在任何振动系统中由于摩擦力总是存在的，所以振动系统最初所获得的能量，在振动过程中因阻力不断对系统做负功，使得系统的能量不断减少，振动的强度逐渐减弱，振幅也就越来越小，以至于最后振动停止，像这样的由于摩擦力转化成内能逐渐减少，振幅随时间而减弱，称为阻尼振动。当振动速度不大时，介质粘性引起的阻力与速度一次方成正比，这种阻尼称为粘性阻尼，通常是用不同频率的阻尼比ξ来表征系统的阻尼，也称为粘性阻尼因子。当ξ<1时称为小阻尼情形。

(1) 小阻尼对周期和频率的影响

(1)

在工程结构问题中，若ξ<0.2，可近似取：ωd=ωn，Td=Tn。

(2) 小阻尼对隔振效率的影响

根据隔振理论，传递系数TR与振动系统的阻尼比ξ，频率比λ有关[1]：

(2)

根据公式(2)得出振动传递系数和频率比的关系图，由图1可知，系统阻尼影响隔振效率，随着阻尼比增加，不同频率比的隔振效率都以相同幅度下降。主动隔振中当采用金属弹簧做弹性元件时，由于金属弹簧的阻尼比极小(约为0.005)，计算隔振效率可以忽略阻尼，而对计算结果影响不大。

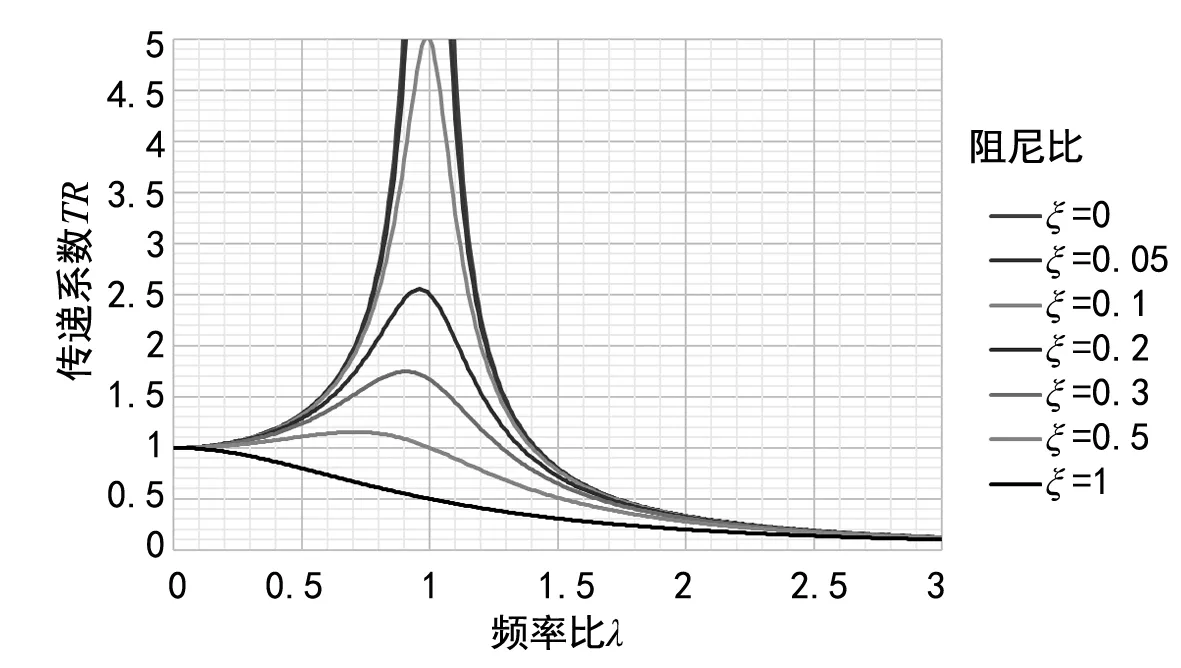
图1 振动传递系数和频率比的函数关系图

因此当采用金属弹簧做隔振元件时，由于金属弹簧的阻尼系数很小，对计算结果影响不大，可以忽略不计。

1.2 隔振原理

在结构中使用减震器是常用的减小振动的方法，是以弹性支撑代替振源与基座之间的刚性连接。图2为物体振动和传递给基座力的关系图，一般称为隔振系统。

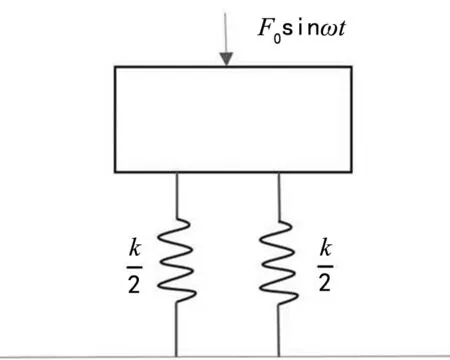
图2 隔振系统

假设风机的不平衡转动引起周期性干扰力F0sinωt，风机的质量为m，k是弹簧的刚性系数，在忽略阻尼的情况下，该振动系统的方程有[2]：

运动方程式为：

mx″ +kx=F0sinωt

(3)

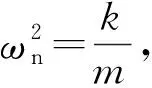
(4)

式中：ω是旋转体的角速度;ωn为无阻尼系统的固有角频率。

在实际应用中只考虑传递给底座的最大作用力，即当sinωt=1时的外力为：

(5)

在振动领域，通常将Fmax与静力F0的比值定于为传递系数或传递比TR，表示传到基础上的力是原振动力的百分之几，如果物体直接固定在基础上，那么振动力就全部传到基础上。

(6)

引入频率比λ：

(7)

(8)

式中：f是工作频率；Fn是减震器的固有频率，并与ω有如下关系：

ω=2πf

(9)

根据图3得出以下结论：

图3 传递比与频率比的关系函数图

隔振效率η：

η=(1-TR)%

(10)

隔振效率的实际含义是振动力被隔离掉百分之几，比传递系数更为直观，因而在实际隔振设计中通常都采用隔振效率描述隔振效果。

为了得到有效的隔振效果通常取λ=5 代入公式(8)和式(10)得：

TR≈0.042

η=95.8%

因此当减震器的固有频率小于工作频率的1/5 时，减震效果达到95.8% 以上，即：

(11)

另外，单个弹簧减震器的载重范围为：

(12)

式中：W为机组总重量；N为弹簧减震器的个数。

综上所述，为风机产品选择弹簧减震器时应当合理选择弹簧减震器的最大载荷以及弹簧减震器的固有频率Fn，就可以达到所期望的减震效果。

2 设计与计算

(1) 组总重量W：为风机重量与基座重量之和w1+w2

风机重量w1：由于风机是采购而来，因此风机的重量可从供应商提供的图纸查出或者在实验室通过测量样品得出。

基座重量w2：基座是本公司自行设计的，没有现成实物，可根据Creo计算出来。 基座重量及重心计算方法如下:

① 依次为每个零件选择材料，见图5。

图5 零件属性

从下列窗口中(见图6)选择所需要的材料，一般为普通钢铁。

图6 材料选择窗

② 通过Creo自动算出重量以及重心位置，见图7。Analysis >> Mass Properties,选择默认坐标。

图7 质量属性

③ 读取窗口中显示出组件的总量以及重心坐标位置，见图8。

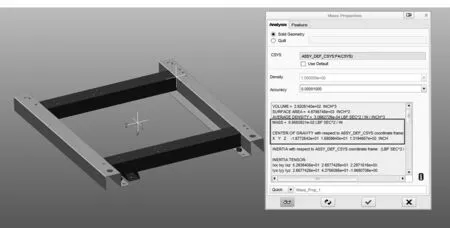
图8 质量属性计算结果

(2) 分配到每个弹簧减震器的载荷F

① 双侧几何对称分布见图9：重心靠近几何中心

F=W/N

(13)

式中：N为弹簧减震器的个数。

图9 双侧几何对称风机

② 单侧几何对称分布见图10：重心靠近几何中心

F1+F2=W/2

(14)

F1×L1=F2×L2

(15)

式中：L1和L2分别是前后弹簧受力点到重心的等效力臂的长度，重心位置可以参考图8中显示的基座重量及重心位置得出。

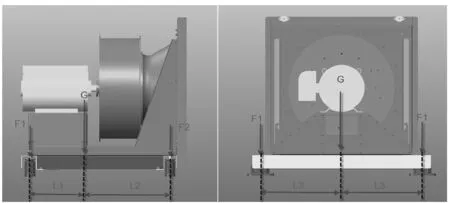
图10 单侧几何对称风机

(3) 计算每个弹簧的静变形ds

ds=F/k

(16)

式中：k为减震器弹簧的刚性系数。

(4) 计算风机工作频率f

(17)

式中：n为风机每分钟转速，其单位为r/min。

(5) 计算弹簧减震器的固有频率Fn

(18)

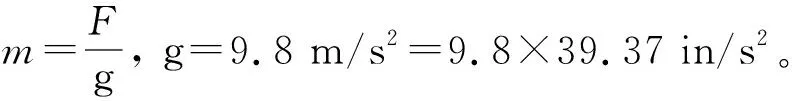
3 风机弹簧效率计算例子

以25冷吨机组所配风机为例子计算校验选择的弹簧减震器是否合适，采用的是单侧几何对称分布计算。

已知条件：

马达参数: 马力20 HP，级数4P，最低转速1 000 r/min。

计算得出:

根据2.1的方法计算出机组总重量：

W=250 (lb)

由Creo计算出机组重心，得：

L1=11(in),L2=19.4(in)

根据公式(14)和(15)，得出：

F1=80 (lb)，F2=45 (lb)

因为所受载荷不同，选取不同减震器弹簧的刚性系数：

k1=88(lb/in)，k2=50 (lb/in)

由弹簧的静变形由公式(16)，得出：

ds1=0.9(in),ds2=0.9 (in)

风机工作频率由公式(17)，得出：

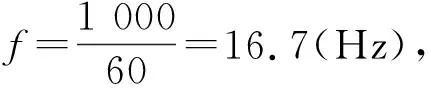
弹簧减震器的固有频率由公式(18)，得出：

Fn1=3.28(Hz)Fn2=3.29(Hz)

验证弹簧减震器的减震效果，满足下面公式：

单个弹簧减震器的载重范围为：

单个弹簧减震器载荷都小于载重范围。因此，选择的弹簧减震器能满足此款风机的载荷，并能达到95.8%的减震效果。

4 结 论

(1) 在计算非对称几何弹簧减震器载荷的过程中，需要分别计算每个弹簧减震器的载荷，而不能轻易按弹簧减震器的数量来均分。

(2) 除了载荷外，还要考虑弹簧减振器固有频率，以此来校验所需弹簧减震器的刚度，从而来验证是否得到所需的减震效果。

(3) 如果验算未能达到预期要求，可以采取以下措施：①加大基座重量或增加弹簧减震器的数量使达到载重要求；②选取较低弹簧减震器的刚性系数使之达到预期的减震效果。