多级离心泵-电机轴系转子动力学分析*
2019-01-18李方忠陈平伟王天周马文生王绍明
李方忠,陈平伟,王天周,马文生,王绍明
(1.重庆水泵厂国家级企业技术中心,重庆 400033; 2.中国航发沈阳发动机研究所,辽宁 沈阳 110015)
0 引 言
现在的旋转机械结构,无论是军用航空发动机还是民用水泵系统,都有着高转速、高效率的发展趋势,结构也相对越来越复杂。作为生产装置的重要辅机,高速多级离心泵在石油、化工、电力和钢铁等重要行业得到广泛应用,随着生产装置的大型化泵机组的单机容量也在不断增大,有时不可避免的要跨越一阶临界转速,甚至还会出现跨越二、三阶或更高阶临界转速的情况。对转子运转的可靠性要求也越来越高、越加严格。研究者采用传递矩阵法和有限元法对临界转速及影响做了大量工作[1-5]。相关文献[6]~[7]对离心泵的计算分析主要集中在叶轮转子的模态分析上。文献[8]主要总结了转子动力学计算方法并采用一维梁单元计算了湿态下水泵的临界转速。考虑到泵机组由驱动电机驱动,驱动电机和泵机转子具有相互耦合作用,共同构成了复杂转子轴系。随着效率和工作转速的提高,整个泵-电机轴系的动力学设计尤为重要。相关文献对此研究并不多见。
以离心泵-电机为研究对象,首先采用MADYN2000分析软件,对离心泵流体密封结构刚度和阻尼进行了计算,最后采用ANSYS软件建立了三维泵-电机转子轴系有限元模型,考虑了转子陀螺效应的影响,分别对在干态和和湿态情况下泵-电机转子轴系临界转速和转子应变能进行了分析。
1 密封特性分析
典型的水泵转子密封结构如图1所示。
密封环内形成的流体力通常采用线性模型计算。其径向力和切向力分量由刚度k、阻尼c、以及质量m的系数描述。转子振动引起的流体力通常由下面方程描述[9]。
(1)

图1 密封结构示意图
转子各级叶轮口环和前后密封的刚度和阻尼采用Black &Jenssen的公式计算,在MADYN2000软件密封刚度计算工具中输入直径间隙、间隙长度、间隙两端压差等参数即可计算得到刚度和阻尼,图2给出了叶轮后密封的密封刚度和阻尼随转速曲线如图2,其中3 500 r/min时密封刚度和阻尼如表1所示。

图2 刚度和阻尼变化曲线

密封位置Kxx(N/m)Kxy(N/m)Cxx(N·s/m)Cxy(N·s/m)叶轮前密封1.2e67.8e51.1e3201叶轮后密封4.6e52.3e563013.5长螺旋主密封1.4e72.3e74.32e61.16e5
2 轴系模型及计算结果
2.1 轴系三维有限元模型
某多级离心泵转子由八级叶轮组成,每级叶轮前后均有迷宫密封结构,还有长螺旋主密封。其中叶片采用公式(2)、(3)中质量、转动惯量等效原则,指定等效圆环的厚度与叶轮外缘处厚度相同,调整相应的外径和密度即可。在ANSYS软件中轴承参数采用combi214单元模拟。
(2)
m=π(R2-r2)hρ
(3)
式中:r为等效圆环内径;R为等效圆环外径;h为等效圆环厚度;ρ为等效圆环材料密度。
电机与多级离心泵驱动端采用碟片联轴器连接,传递扭矩。在有限元模型中可施加弹簧单元来模拟工程中非完全刚性连接。建立的离心泵-电机三维转子轴系有限元模型如图3所示,模型左边为多级离心泵,采用两端支撑,右边为电机转子,采用两端支撑方式,中间为简化的联轴器结构。

图3 泵-电机轴系实体单元模型
2.2 干态下临界转速及转子应变能
在不考虑密封刚度和阻尼情况下,计算了干态下泵-电机轴系的临界转速和转子应变能分布,计算中考虑了转子陀螺效应的影响,临界转速坎贝尔图如4,前四阶临界转速振型及转子应变能分布如图5~8所示,其中应变能图为结构半剖图,表2给出了临界转速值及泵转子、联轴器和电机转子的应变能。
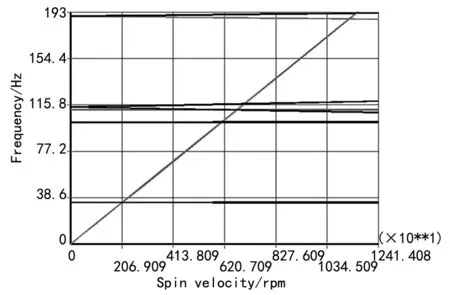
图4 干态下临界转速坎贝尔图
由图4和表2中可以看出,在干态下第一阶临界转速为2 083 r/min,振型为泵转子弯曲型,轴系应变能主要分布在泵转子轴上中间部分,该振型对叶轮不平衡量比较敏感,而泵转子的主要不平衡量集中在叶轮,应加强叶轮的平衡精度控制。第二阶临界转速为6 069 r/min,振型为电机转子弯曲型,转子应变能主要集中在电机转子上,占51.7%,随着轴系转速的升高,应同时关注电机的振动情况。第三阶和第四阶振型均为泵转子弯曲,在这里不在叙述。

表2 轴系临界转速及应变能

图5 第一阶振型及应变能分布

图6 第二阶振型及应变能分布
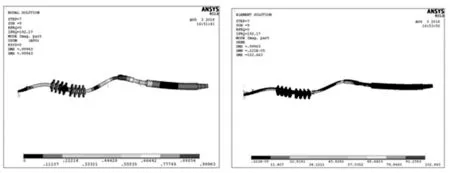
图8 第四阶振型及应变能分布
2.3 湿态下的临界转速及转子应变能
在考虑密封刚度和阻尼情况下,计算了湿态下泵-电机轴系的临界转速和转子应变能分布,并分析了轴系的稳定性。临界转速坎贝尔图见9所示,在零频时出现了分叉,这是因密封刚度的影响。图10给出了有限元求解特征值实部解,实部均为负数,表示转子系统是稳定的。前四阶临界转速振型及转子应变能分布如图11~14所示,其中应变能图为结构半剖图,表3给出了临界转速值及泵转子、密封结构和电机转子的应变能。
湿态下第一阶临界转速为5 746 r/min,振型为泵转子弯曲型,轴系转子应变能占50%左右,其中离心泵转子应变能占32.6%,其余应变能主要分布在密封盒轴承上。第二阶临界转速为6 130 r/min,振型为电机转子弯曲型,转子应变能主要集中在电机转子上,占51%。第三阶和第四阶的主要系统应变能主要集中在轴承和密封结构上,转子上的应变能为30%左右。

图9 湿态下临界转速坎贝尔图
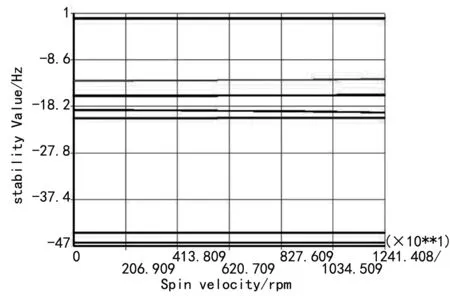
图10 特征值实部

阶次临界转速(r/min)泵转子应变能(%)密封单元应变能(%)电机转子应变能(%)第一阶5 74632.610.515.7第二阶61.30.60.151第三阶8 3022129.411.7第四阶8 8642226.310.7

图11 第一阶振型及应变能分布

图12 第二阶振型及应变能分布
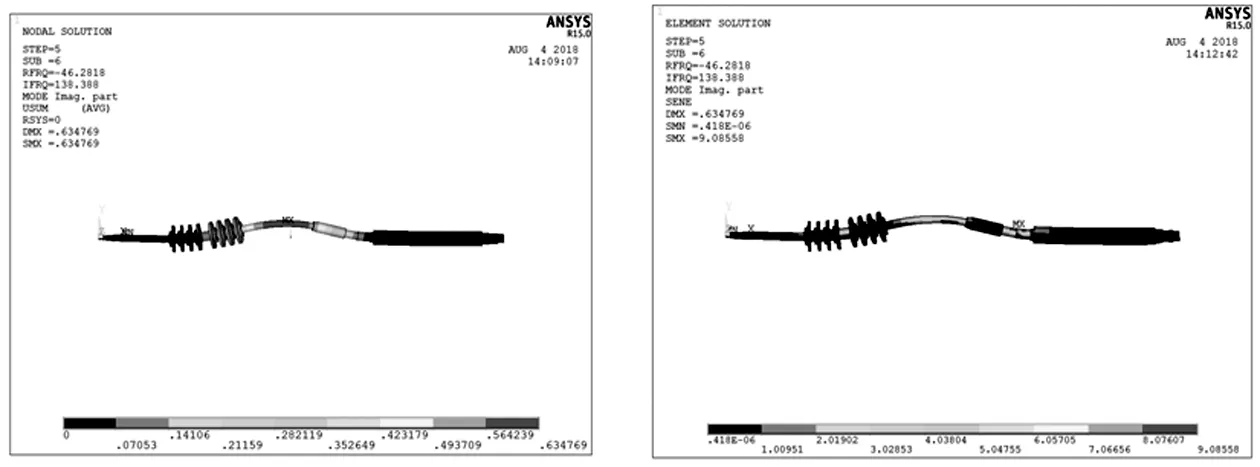
图13 第三阶振型及应变能分布

图14 第四阶振型及应变能分布
3 结 论
针对多级离心泵-电机系统,建立了三维转子有限元模型,计算了干态和湿态情况下前四阶临界转速和应变能。
结果发现湿态情况下第一阶临界转速有所增大,第二阶临界转速振型主要以电机弯曲为主,随着离心泵-电机轴系工作转速的增加,应加强对电机振动情况的关注。
由于密封刚度和阻尼的作用,前四阶整个轴系转子的应变能从有所下降,最高下降了20%左右。但前四阶轴系转子应变能还是具有偏大的特点。
转子应变能的分布可以了解离心泵-电机转子轴系结构设计中的薄弱环节,有利于相应的结构改进设计。
