基于叶尖定时原理的转子叶片同步振动算法研究*
2019-01-18雷晓波
雷 杰,雷晓波
(中国飞行试验研究院 发动机所,陕西 西安 710089)
0 引 言
旋转机械叶片是航空发动机旋转部件的关键零件,长期工作在高压、高温、高转速等恶劣环境下,受到离心力、气动力等作用,容易产生振动。如果旋转机械叶片出现异常振动,就可能导致裂纹出现甚至断裂,造成严重事故[1],所以叶片振动特性研究一直是航空发动机设计、使用中重点关注的问题,非常有必要对旋转机械叶片振动进行在线检测,实时监控叶片是否存在异常振动,目前转子叶片振动常规测量方法是在叶片上粘贴一定数量应变计,然后通过引电器把信号引到外部进行测量[2],此方法属于接触式振动测量方法,技术比较成熟,但应变计的粘贴工作繁琐且很难做到监测所有叶片振动情况,此外受工作环境等因素影响,传感器工作寿命较短,制约了该类技术在叶片振动实时监测方面的应用。为此国内外都开展了非接触振动测量方法研究,主要方法包括:频率调制法、间断相位法[3]、光线自追踪法[4]、声响应法[5]、叶尖定时测量法[1-2,6-9]。其中基于叶尖定时原理的非接触振动测量技术是研究的热点之一,克服了传统应变片法安装复杂、可靠性低、寿命短等缺点[10],其基本原理是沿径向在旋转机械静止的壳体上安装叶尖定时传感器,测量叶片旋转时通过叶尖传感器时所产生的脉冲信号,记录叶片到达传感器的透过时间[11]。由于叶片受振动影响,使得测量的脉冲信号会发生微小的提前或滞后,结合叶片半径、转速可实时测量叶尖的振幅,然后通过一定算法可推导出叶片同步共振的参数信息。
目前该测量技术硬件部分已经能满足测量需要,主要研究方向集中在传感器布局和振动信号重构算法研究上。为此,以简化叶盘为研究对象,开展了基于叶尖定时原理的转子叶片同步振动算法研究,利用三角函数和最小二乘法建立了振动重构算法,并利用数值仿真对重构算法进行了验证。
1 叶片同步振动重构理论及算法
叶片同步振动是指叶尖振动频率ω是转速频率Ω的整数倍,即ω=NΩ,N为自然数。根据叶尖定时测振原理,在转轴上安装一支转速同步传感器,在叶片顶端机壳上分布n支叶尖定时传感器TIP(n=4~9)。在转子单个旋转周期内,同一叶片经过每支传感器一次,单个传感器对同一叶片振动的采样频率相当于转速频率,n支叶片传感器也只能采集同一叶片n个离散的脉冲信号序列,采样频率取决于转子转速和传感器数量。显然叶片振动信号采样频率远小于叶片的振动频率,根据香农采样定理可知,叶片的振动波形是无法通过单个或者多个传感器叶尖传感器直接获取,需要设计一种辨识方法,利用多个传感器测得位移值的差异辨识出叶片同步振动参数。
1.1 基于单自由度振动原理的算法
转子叶片振动信号可用多个简谐振动叠加而成:
(1)
式中:m为谐波数量;y为振动位移;Ai为各谐波幅值;φi为各谐波初始相位;g(t)为随机噪声或者其他频率成分信号;C为叶片振动平衡位置可能产生的常偏量。考虑到叶片发生同步振动时,叶尖振动频率是转速频率的整数倍,可将转子叶片同步振动运动方程简化为单自由度振动形式。
y=Asin(NΩt+φ)+g(t)+C
(2)
由于同一传感器不同周期测得的叶片振动位移值y保持不变,因此要确定叶片同步振动,必须辨识出A、N、φ这三个参数值。
1.2 叶片同步振动算法重构理论
在机壳上任意分布n支传感器,按转子旋转方向传感器依次编号为1~n,相对1号传感器的安装角分别为α1、α2、α3、…、αn,图1为安装4支传感器时位置示意图。假设叶片发生同步振动时,在一圈时间内叶片振动稳定,转速恒定,根据公式(2)可知不同的叶尖定时传感器采集到叶尖位移值为:
yi=Asin(NeΩti+φ)+g(t)+C
(3)
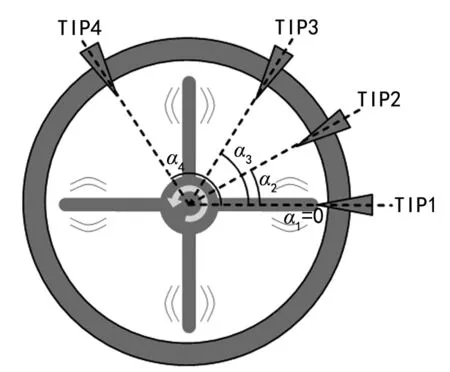
图1 传感器安装位置示意图
由于叶片每周到达同一传感器的时间ti不变,因此同一传感器不同周期测得的叶片振动位移值yi也保持不变。为了便于分析,令叶片经过1号传感器的时刻定为t1=0,忽略叶片本身振动带来的时间误差,该叶片到达其他传感器的时间ti=αi/Ω,则公式(3)可表示为:
yi=Asin(Nαi+φ)+g(t)+C
(4)
公式(4)所示方程组包含n个方程,振动位移yi为测量值,A、Ne、φ、g(t)、C都为未知数,方程组属于超定非线性方程组,其解不易直接求得。为方便求出同步振动参数,将g(t)和C合为C1(t),然后根据三角函数公式,将公式(4)改写为:
yi=Asin(Nαi)cosφ+Acos(Nαi)sinφ+C1(t)
(5)
那么n支传感器测得的叶尖振动位移为:
y1=Asin (φ)+C1(t)
y2=Asin(Nα2)cos(φ)+Acos(Nα2)sin(φ)+C1(t)
y3=Asin(Nα3)cos(φ)+Acos(Nα3)sin(φ)+C1(t)
⋮
yn=Asin(Nαn)cos(φ)+Acos(Nαn)sin(φ)+C1(t)
(6)
将公式(6)进一步改写为矩阵形式:
Y=BX
(7)
式中:Y、B、X分别为:
(8)
公式(7)中向量X为未知向量,包含了A、φ和C1(t)等3个未知数,矩阵B作为系数矩阵,只包含了1个未知参数N。如果N已知,可通过最小二乘法对其求解得到A、φ和C1(t)。由于振动倍频N值是一个自然数,并且转子叶片振动可能产生的倍频值也是有限的,在旋转机械设计时,已经基本估计出所有的主要振动倍频范围。因此选取一定的N范围(一般取1~30),对其进行遍历,将可能的N值代入到式(7)中,根据最小二乘法进行求解:
Xk=(BTB)-1BTY
(9)
将Xk与实测振动位移Y的残差定义为:
(10)
考虑实际测量中的存在各种误差,当Sk取最小值对应的N即为实际振动倍频,此方法为倍频遍历法,可计算出叶片同步振动频率fs、幅值A、相位φ等振动参数。
2 数值仿真分析
2.1 振动仿真条件及过程
假设某风扇转子试验器共20支风扇叶片,在风扇壳体上安装了4只叶尖振动传感器,叶尖振动传感器TIP1~TIP4分布角度依次为0°、53°、121°、252°。其中2号叶片固有频率为600 Hz,由于旋转离心刚化效应,叶片共振频率会大于其固有频率,设叶片同步共振频率为603.3 Hz。其中风扇转子在6 030 r/min运转时TIP1~TIP4叶尖振动传感器位移都明显比其他转速下大,考虑到叶片弯曲扭转造成的载荷、振动以及噪声的共同影响,设叶片振动信号表达式为公式(12),对应的叶片振动原始波形见图2。
(12)
式中:叶片共振幅值为1 000 μm、频率为603.3 Hz、初始相位为4π/9,为方便理解分析,设定零时刻2号叶片到达TIP1位置,到达TIP1位置时叶片相位为4 π/9。根据叶片频率振动成分组成,引入幅值30 μm、频率40.5 Hz的振动成分,其振动初始相位为-π/5;存在约为叶片共振频率幅值10%的振动成分,幅值为100 μm,频率为153.5 Hz,振动初始相位为π/4;加入高斯白噪声及静载荷产生的50 μm的位移量。
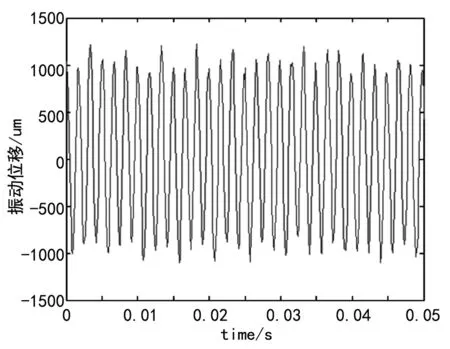
图2 叶片振动原始波形
根据传感器之间的安装角度差,可以推算出2号叶片到达各传感器时刻的时间差,该时间差会导致风扇叶片振动信号相位相应改变,准确来说同步振动相位差将是角度差的6倍,叶片同步振动信号其他成分也会发生相应的改变,那么2号叶片依次经过传感器TIP1~TIP4时得到的振动信号表达式依次为:
(13)
53/180/201×307π)+50
(14)
121/180/201×307π)+50
(15)
252/180/201×307π)+50
(16)
对于2号叶片振动信号,转子每旋转一圈,TIP1~TIP4传感器只能各采集一个脉冲信号。通常非接触数据采集系统会一次采集0.2 s的数据进行处理,那么在0.2 s时间内每支传感器可以采集约20个脉冲信号序列,其波形如图3所示。

图3 TIP1~TIP4传感器拾取的振动位移
可以看出由于其他振动信号及噪声的引入,TIP1~TIP4各个传感器拾取的数据点波动是较大的,达到了同步振动幅值的20%~40%,对比同一时刻TIP1~TIP4数据点的大小可以看出传感器的位置对于数据采集和后期处理有较大影响。
采用倍频遍历法寻找倍频数N,图4为振动位移拟合误差随倍频数的变化曲线,根据图4可以看出不同倍频数的振动位移拟合误差不同,绝对误差较大。其中拟合误差最小值为0.761 μm,对应的N为15,取N=15时计算的振动幅值为352.6 μm,显然结果不对,多次仿真结果依然出错。分析公式(13),可以看出每个传感器采集曲线与其安装位置、原始信号成分组成有关,辨识结果出错原因可能与传感器安装位置有关,下面通过改变传感器安装角度分析出错原因。
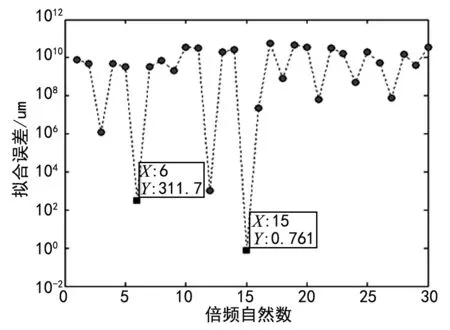
图4 拟合误差随倍频数的变化曲线
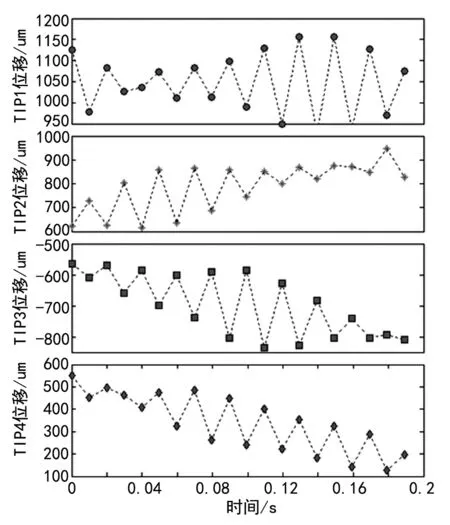
图5 TIP1~TIP4传感器拾取的振动位移
2.2 改变传感器安装角度的辨识结果
将TIP3安装角度改为143°,四支传感器拾取的振动位移曲线见图5,利用倍频遍历法寻找倍频数N,图6为改变TIP3传感器安装角度后振动位移拟合误差随倍频数的变化曲线。
根据图5可以看出TIP1~TIP4每支传感器拾取的离散点波动依然较大,并没有因角度改变而发生减小。从图6可以看出N=6时,振动位移拟合误差最小,因此可判定该同步振动频率为风扇叶片转频的6倍频,即叶片共振频率为603 Hz,与上文假设条件吻合。通过最小二乘法计算出的同步振动参数及误差,具体见表1,其中幅值为995.32 μm,误差为4.68 μm,误差很小,但初始相位与真实初始相位相差10.48°,误差较大。通过大量仿真发现:不论其他振动成分幅值多小,静态偏移和噪声量多小,其相位辨识的误差并未有改善,这与相位的求解方法有较大关系。
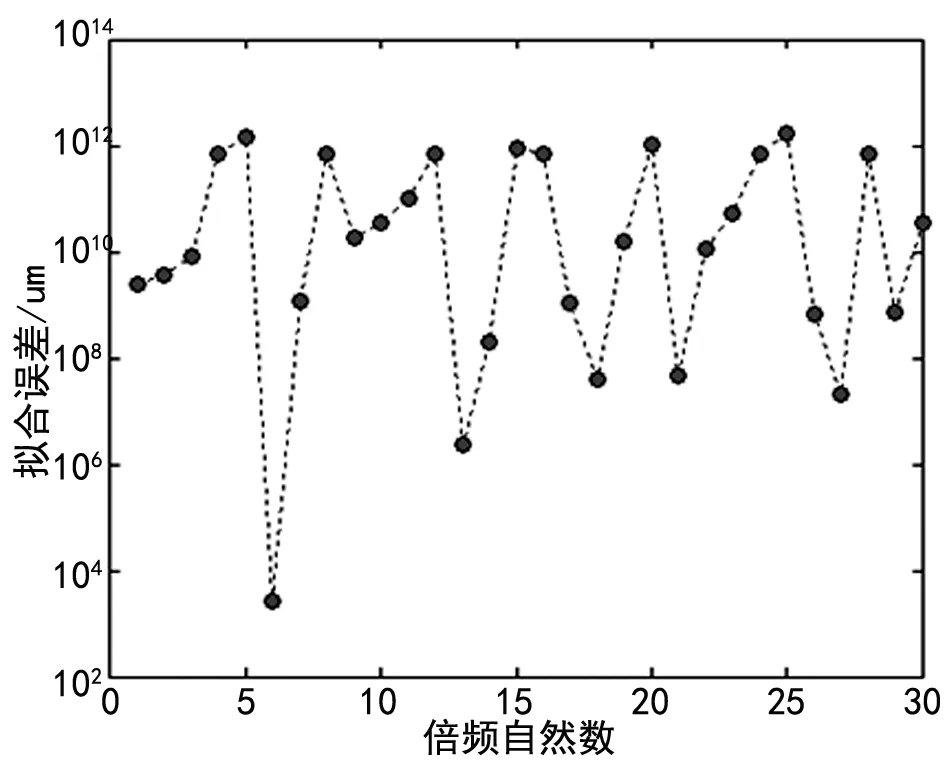
图6 拟合误差随倍频自然数变化曲线
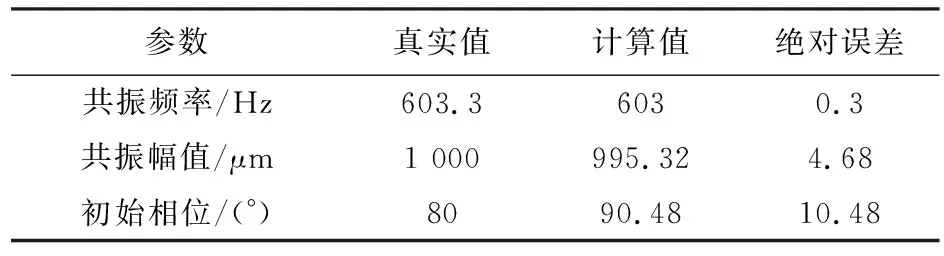
参数真实值计算值绝对误差共振频率/Hz603.36030.3共振幅值/μm1 000995.324.68初始相位/(°)8090.4810.48
2.3 改变其他信号幅值的辨识结果
将公式(12)中153.5 Hz频率成分的幅值由原来的100 μm改为20 μm,其TIP1~TIP4传感器拾取的离散振动数据曲线为图7所示,振动位移拟合误差随倍频数的变化曲线如图8所示。
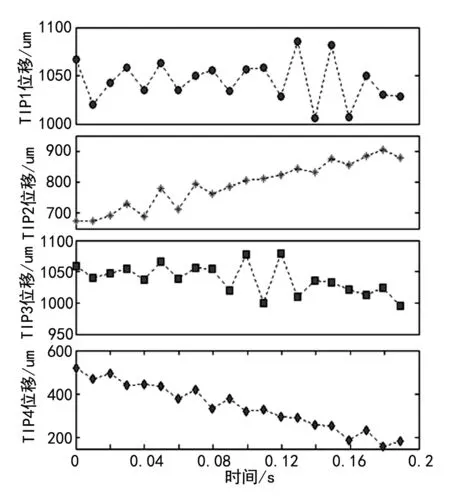
图7 TIP1~TIP4传感器实时振动位移波形
当N=6时,振动位移拟合误差最小,同步振动频率为风扇叶片转频的6倍频,即叶片共振频率fs为603 Hz。通过最小二乘法得出的同步振动参数及误差如表2所列,幅值为1 007.2 μm,误差为7.2 μm,可以看出误差小,但初始相位与真实初始相位误差还是较大。
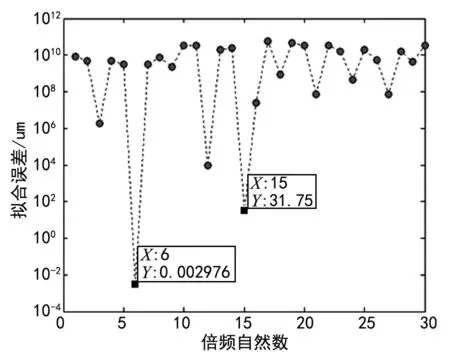
图8 拟合误差随倍频数的变化曲线
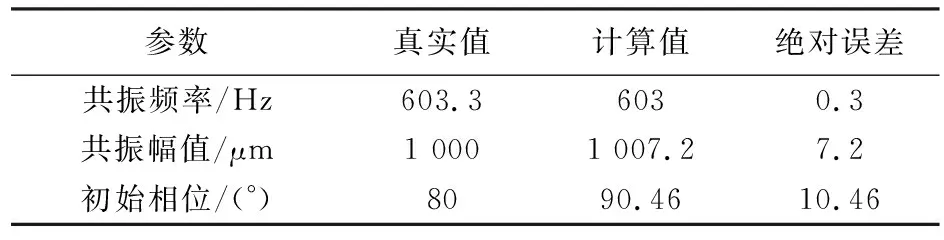
参数真实值计算值绝对误差共振频率/Hz603.36030.3共振幅值/μm1 0001 007.27.2初始相位/(°)8090.4610.46
3 结 论
对叶片同步振动算法理论和算法实现过程进行了详细阐述和推导,利用数值仿真对重构算法进行了大量验证,发现了同步振动算法的部分弊端,仿真结果表明:
(1) 该算法可以精确辨识出叶片振动倍频和幅值,但对振动相位辨识误差较大。
(2) 传感器角度布置是否合理,会影响算法辨识的成功与否,在实际工程中可以通过调整传感器布置角度分布,确定验证振动参数辨识的准确性。
(3) 较大的其他振动频率成分和噪声信号,会导致算法辨识出错,针对这种情况,除了寻找新的方法外,可采用改变传感器布置角度来弥补非同步振动频率成分的影响。
