十字轴万向节从动节叉叉头应力有限元分析*

高文才，韩晓强，陈贵春

(1.神东煤炭集团机电管理部，陕西 榆林 719315； 2.莱州亚通重型装备有限公司，山东 莱州 261400)

0 引 言

当车辆采用前桥转向、四轮驱动行驶时，连接前轮及传动轴的万向节不仅要配合转向前桥转向油缸实现转向功能，而且需要传递驱动扭矩，实现四轮驱动。因此前桥万向节一旦出现断裂失效等问题，将直接导致车辆无法行驶，对于工程车辆，前桥转向节出现问题将导致严重的后果。因此在进行车辆设计时，转向节的选型核算是极为重要的一环。笔者涉及的混凝土搅拌运输车为发动机前置，分时四驱。在某矿采用四驱方式行驶时，前桥双十字轴万向节从动节叉叉头发生扭曲变形进而断裂的现象，为避免类似问题再次发生，笔者计算了混凝土搅拌运输车前桥采用的双十字轴万向节最大承载扭矩。在此基础上，结合有限元法计算了断裂的双十字轴万向节从动节叉叉头的应力分布规律。若在车辆设计阶段进行核算，可有效地避免事故的发生。

1 传动轴最大理论承载扭矩计算

传动系统传递到传动轴的驱动力矩若大于地面附着力的阻力矩，驱动轮将出现打滑现象[1]，因此传动轴的最大驱动力矩设计为略小于或等于地面附着力的阻力矩。由于本文研究的混凝土搅拌运输车采用手动变速箱，传动轴最大理论承载扭矩为其最大驱动力矩TFmax。传动系统及发动机参数如表1所示。

表1 传动系统及发动机参数

取齿轮传动效率ηc为0.98，手动变速箱、分动箱、驱动桥主减速器均为二级齿轮传动，分动箱处前后桥扭矩分配为50:50，中间传动轴扭矩传递效率为0.98[2]，则根据图1所示驱动扭矩传递路径，传动轴最大理论承扭矩计算公式为：

(1)

因此左右传动轴单独受到的最大承载扭矩TFmax=4 598 N·m。最大承载扭矩TFmax通过双十字轴万向节传递到前桥短半轴，带动车轮旋转。

图1 混凝土搅拌运输车扭矩传递路径1.发动机 2.离合器 3.手动变速箱 4.中间传动轴 5.分动箱 6.前桥主减速器 7.前桥长半轴 8.双十字轴万向节 9.前桥短半轴

2 双十字轴万向节受力分析

对于单十字轴万向节，当主从动节叉相对旋转时，某一瞬间如图2所示。主动节叉上一点运动轨迹在垂直主动轴的平面上投影为圆形，从动节叉上一点B在同一平面上运动轨迹投影为一椭圆。节叉OA垂直于OB，因此当主动节叉转角为φ1时，A在投影面上由A0旋转至A1，B0旋转至B1，OB1仍然垂直于OA1，即∠B0OB1=φ1。将OB1所在的平面旋转角α，使其与OA所在的平面重合，这时OB1成为OB1′，B1′点所对应的中心角∠B0OB1′即为从动节叉的轴叉上B点的实际转角φ2，由几何关系可得：

cosα=tanφ1/tanφ2

(2)

tanα=tanφ1/cosα

(3)

式中:α为两万向节叉间夹角；φ1、φ2为主从动节叉转角。

可见，单十字轴万向节主从动节叉转角不相等，主从动节叉角速度存在周期性波动[3]。

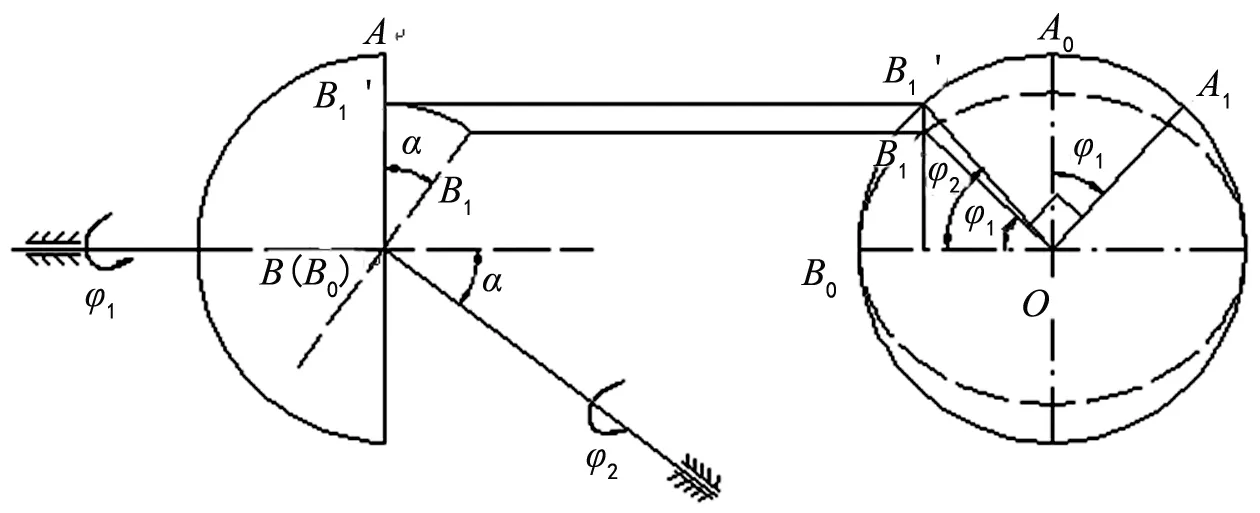
图2 单十字轴万向节传动关系

为了消除十字轴式万向节从动轴的角速度周期性的波动，可将两个单十字轴式万向节串联成为如图3所示双十字轴式万向节。对于本文所研究的双十字轴万向节，平面L1O1L2与L2O2L3之间的传动夹角及中间传动轴两个节叉所在面Ⅰ与Ⅱ的夹角均为零，输入轴与输出轴之间能够实现等速传动[4]。

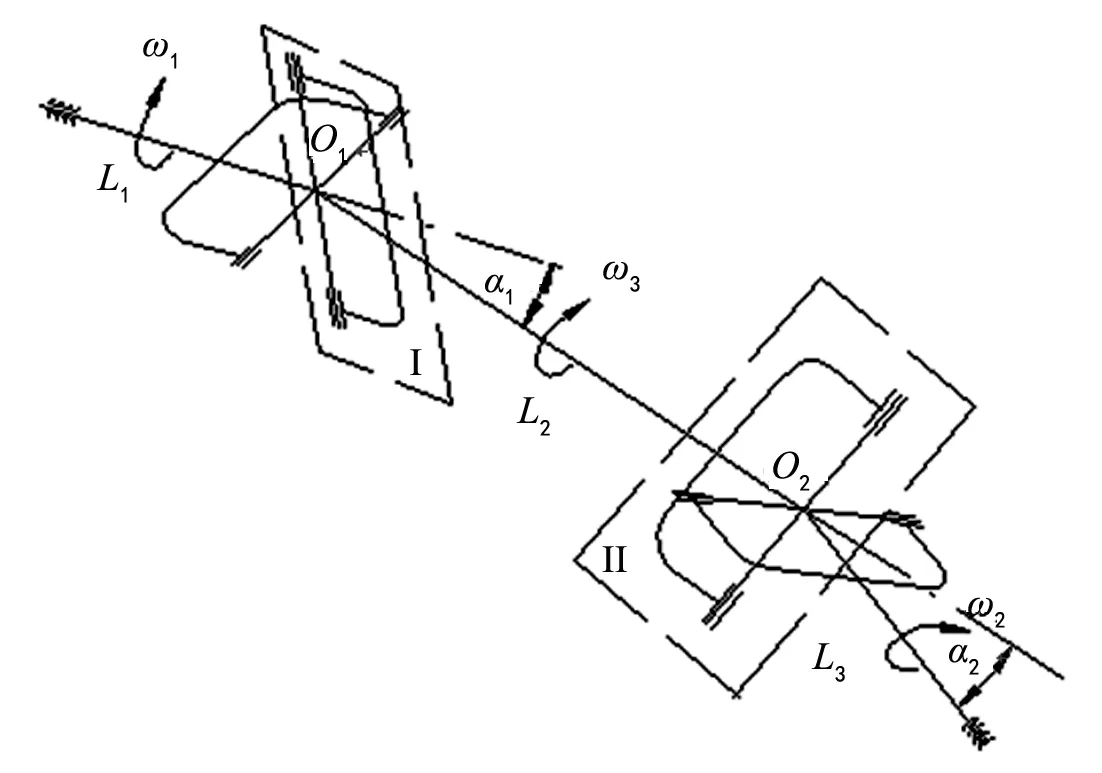
图3 双十字轴万向节示意图

由式(2)及投影关系，可知双十字轴万向节主动节叉、中间节叉及从动节叉转角间关系为:

tanφ1=tanφ3cosα1

(4)

tanφ2=tanφ3cosα2

(5)

式中：φ1、φ2、φ3为主从动节叉及中间节叉转角；α1、α2为主动节叉与中间节叉，中间节叉与从动节叉间的夹角。

公式(4)、(5)两侧同时对时间求导，可得：

(6)

(7)

由公式(6)、(7)可得主从动节叉角速度关系：

(8)

根据瞬时功率不变原理，主动节叉扭矩为T1，从动节叉扭矩为T2，则：

(9)

当α1、α2范围为0～20°时，从动节叉扭矩T2的数值范围为：0.9397T1≤T2≤1.0642T1。由于T1、T2差距不大，因此认为主从动节叉扭矩相同。

3 万向节从动节叉应力计算

3.1 有限元模型建立

实际万向节断裂部位发生于万向节叉从动节叉处，因此在建立有限元模型时，进行适当的简化，只对从动节叉进行计算，并将中间节叉与十字轴建模为刚体。通过对现场所用万向节进行测绘，对中间节叉、十字轴及从动节叉建立三维模型如图4所示。

图4 有限元模型

十字轴万向节的工作原理为主从动节叉分别以铰链的形式连接中间十字轴，当主从动节叉间夹角不为零时，主从动节叉绕各自轴线转动，带动十字轴做空间运动。因此在有限元模型中，以组合连接属性Hinge连接中间节叉与十字轴[5]，并用相同的连接属性连接中间节叉与地面参考点A，从动节叉扭矩施加点C与地面参考点B。在参考点C施加上文计算的传动轴最大承载扭矩T2=T1=TFmax=4 598 N·m。

为计算从动节叉应力，对十字轴与从动节叉相应接触面定义接触属性，并进行接触分析计算。

从动节叉的材料为20CrMnTi，材料的抗拉强度σb=1 080 MPa，屈服强度σs=835 MPa，弹性模量E=207 GPa，泊松比μ=0.25，伸长率δ5=10%。

分别计算从动节叉与中间节叉夹角为0°、6°、12°时，中间节叉转动带动从动节叉转动一周时从动节叉叉头应力分布。

3.2 计算结果分析

当从动节叉与中间节叉夹角α=0°时，从动节叉叉头最大应力点如图5(a)所示，最大应力点位于叉头上与转向一致侧根部，最大应力值σmax=846 MPa。从动节叉与中间节叉夹角α为6°及12°时，从动节叉叉头应力分布如图5(b)所示。

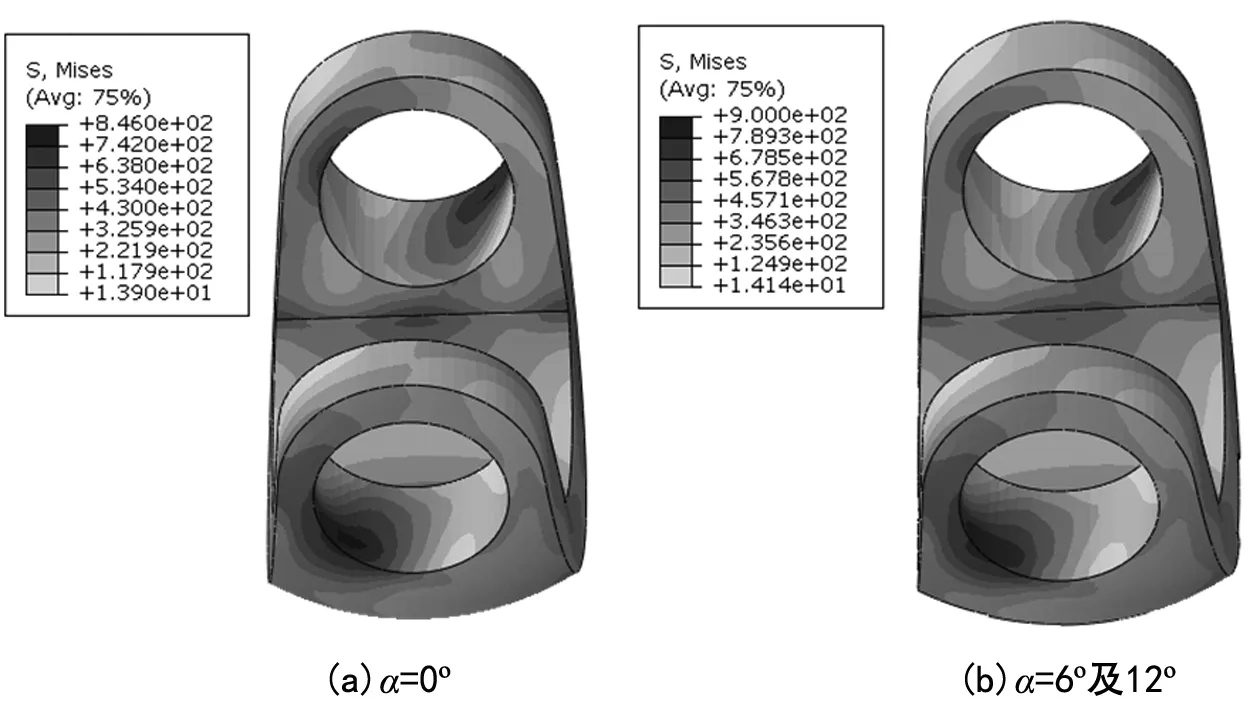
图5 从动节叉叉头最大应力分布

α=0°、6°及12°时，从动节叉两个叉头最大应力σmax随从动节叉转角φ关系曲线如图6所示。由图6可知，当双十轴万向节中间节叉与从动节叉夹角α为零时，最大应力点始终位于与转向一致侧叉头根部，且其值不随转角变化而变化。而当双十轴万向节中间节叉与从动节叉夹角不为零时，从动节叉两个叉头上的最大应力同样位于与转向一致侧叉头根部。由于每个叉头的最大应力随节叉转动呈正弦规律周期性变化，整个节叉叉头最大应力点交替出现在两侧叉头，且最大应力点应力值总体上大于中间节叉与从动节叉夹角为0时最大应力值。当α=6°时，最大应力σmax=877 MPa，当α=12°时，最大应力σmax=900 MPa。

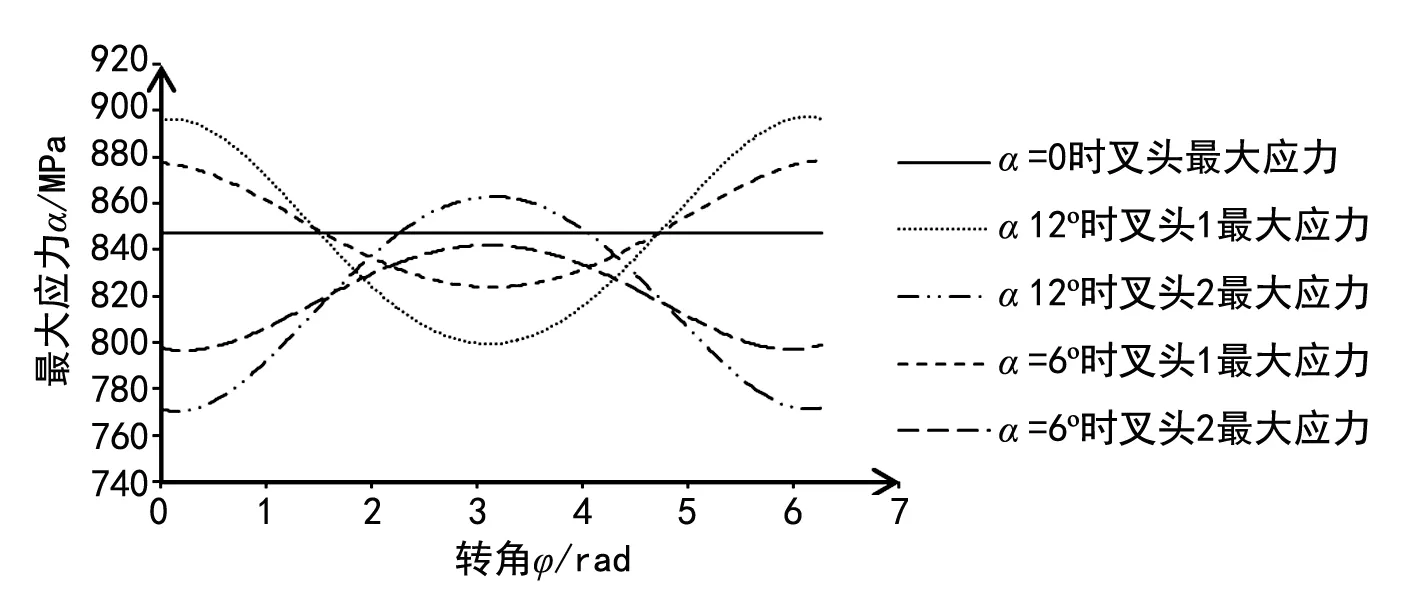
图6 节叉叉头最大应力与节叉转角的关系

由图6可知，当夹角α增大，节叉叉头最大应力值的振幅随之增大，但整个节叉叉头的最大应力随夹角α的增大而增大。

以上计算得到的在不同夹角α下的最大应力，均超出节叉所采用材料20CrMnTi的屈服极限。因此，在双十字轴万向节使用过程中，从动节叉将出现屈服变形，从而导致刚度失效。若由于冲击振动导致节叉断裂时，断裂部位将出现在最大应力区域。节叉现场断裂部位如图7所示，与计算结果比较吻合。

图7 失效从动节叉叉头现场照片

4 结 论

根据罐车传动系统结构，计算了传动轴最大理论承载扭矩。通过对罐车实际采用的双十字轴万向节进行受力分析，将计算得到传动轴传递到从动节叉的最大扭矩作为有限元模型的边界条件。对所采用的双十字轴万向节进行测绘，依据其工作原理，建立有限元模型，对发生断裂的双十字轴万向节从动节叉叉头部位进行应力分析，并研究了其最大应力、从动节叉与中间节叉夹角α、从动节叉转角φ的关系。通过以上计算，得出如下结论：

(1) 双十字轴主从动节叉扭矩T1、T2与中间节叉夹角α1、α2有关，但当α1、α2在0～20°范围时，0.9397T1≤T2≤1.0642T1，可以近似认为相等。

(2) 从动节叉叉头上的最大应力位于与转向一致侧叉头根部，当从动节叉与中间节叉夹角α=0°时，最大应力点位置不变；从动节叉与中间节叉夹角α不为0时，最大应力点随从动节叉转动交替出现在两个叉头与转向一致侧叉头根部。

(3) 而当双十轴万向节中间节叉与从动节叉夹角α不为零时，每个叉头的最大应力随节叉转轴呈正弦规律周期性变化，振幅随角α增大而增大，且整个节叉叉头的最大应力随夹角α的增大而增大。

计算结果与现场节叉失效形式及位置比较吻合，验证了计算的准确性。以上结论表明，在双十字轴万向节选型时，应当校核从动节叉与中间节叉夹角最大时其最大应力，从而在设计阶段规避可能会出现的失效问题。