基于数学建模素养的《正态分布》教学设计

素质教育在传授知识的同时，更加注重能力的培养。数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养。高中生面对实际背景丰富的问题往往无从下手，这就需要在教学中渗透方法，引导学生在实际情境中从数学的视角发现问题、提出问题，分析问题、建立模型，并运用所学知识求解模型。

1 内容解析

正态分布是高中阶段唯一一种连续型分布，课程安排在离散型随机变量及其分布之后，是概率知识的重要组成，又是统计学的基石，在数学、物理、工程等领域应用广泛。

正态分布的教学中要把握以下几个问题：（1）服从正态分布的随机变量的特征；（2）正态分布密度曲线的特点；（3）正态分布的特点。

2 教学目标

（1）观察高尔顿板试验，分析数据分布的特点，建立钟形曲线的直观印象。

（2）理解正态分布密度曲线函数解析式的由来，借助图形分析曲线特点，理解两个参数的含义。

（3）能运用正态分布解决一些简单的问题。

3 教学问题诊断

在高中阶段推导得出正态分布密度曲线有难度，因而需要考虑学生的情况，设置合理过渡帮助学生理解。对于该部分内容的考察不会设置很难的题目，应还原正态分布曲線密度曲线的形成，注重学生数学建模素养的培养。

4 教学过程设计

4.1 情境引入，发现问题

问题1 生活中我们习以为常的偶然现象中往往存在着必然规律。因为各种偶然因素而最终聚在一个班的我们，身边又有什么必然现象呢？列出在课前收集到的全班同学身高数据，如何分析身高的分布情况？

设计意图 对于实际问题，可以用数学方法建立模型，描述其特点。引导学生画频率分布直方图分析数据，总结数据的分布特点：中间多，两边少。让同学们列举生活中同样具有这样形态特点的现象，激发学生的好奇心，去积极探索偶然现象中的必然规律。

4.2 讲授新知，分析问题

问题2 达尔文的《物种起源》问世后，他的表弟高尔顿（Galton，1822-1911）同时也是生物统计学派的奠基人，尝试用统计方法研究遗传进化问题，设计了一个叫高尔顿板的装置模拟这种现象。

装置介绍：如图1所示，一块木板上钉着若干相互平行且相互错开的圆柱形小木块，小木块之间留有适当的空隙作为通道，前面挡有一块玻璃。

让小球从上方通道口落下，与层层的小木块碰撞，最终落入下方的某一球槽中。打开高尔顿板试验模拟器，运行后模拟结果如图1所示，引导学生建立横、纵坐标，继续使用频率分布直方图来分析小球分布情况。

设计意图 正态分布的模拟需要大量数据，课堂上不好实现，高尔顿板是一个很好的载体。对数学史进行简单介绍，增强学生学习兴趣，有利于主动参与解决问题。对于数据特征并不明显的实际问题，我们也可以寻找切入点，合理建立分析模型，实现数学化，运用所学，转化为已知问题。

问题3 如果在高尔顿板试验中，增加小球数量，试验结果会呈现什么特点？如何分析小球的分布？在使用频率分布直方图时，应该做怎样的调整？

设计意图 对于直观看到的实际问题，使学生熟悉数学化的方式，养成数学建模分析问题的习惯。学生对于正态分布密度曲线的得到是教学难点，结合试验演示，观察实验数据分布变化特点，合理引出，理解曲线与频率分布直方图之间的联系。

问题4 结合刚才的分析，正态分布密度曲线有什么特点呢？

设计意图 让学生把握正态分布密度曲线的特点：

（1）位置：轴上方，与轴不相交；

（2）对称性：单峰，关于直线对称；

（3）峰值：在处达到峰值；

（4）曲线与轴之间的面积：1.

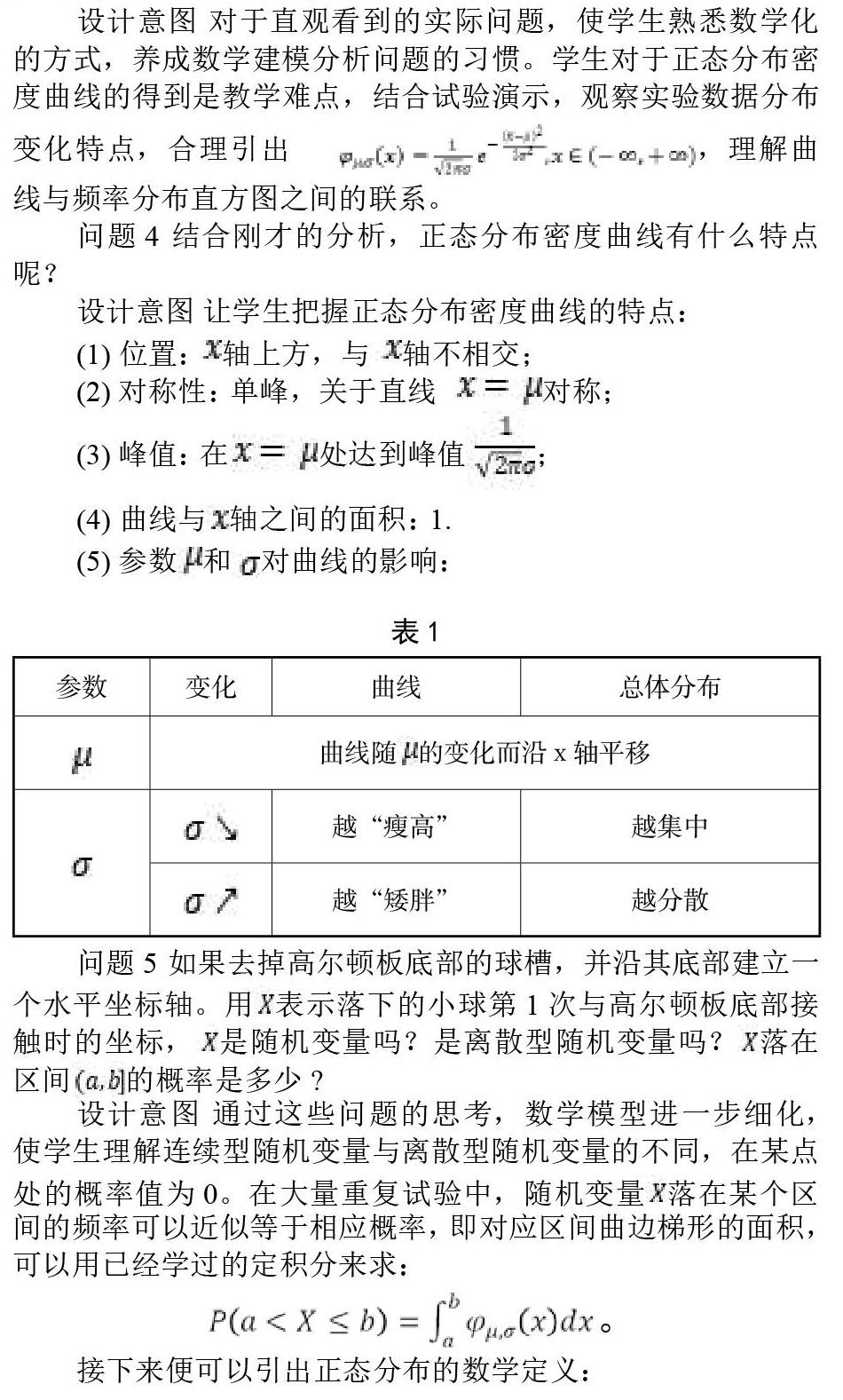
（5）参数和对曲线的影响：

问题5 如果去掉高尔顿板底部的球槽，并沿其底部建立一个水平坐标轴。用表示落下的小球第1次与高尔顿板底部接触时的坐标，是随机变量吗？是离散型随机变量吗？落在区间的概率是多少？

设计意图 通过这些问题的思考，数学模型进一步细化，使学生理解连续型随机变量与离散型随机变量的不同，在某点处的概率值为0。在大量重复试验中，随机变量落在某个区间的频率可以近似等于相应概率，即对应区间曲边梯形的面积，可以用已经学过的定积分来求：

接下来便可以引出正态分布的数学定义：

一般地，如果对于任何实数，随机变量满足

则称随机变量X服从正态分布。正态分布完全由参数μ和σ确定，因此正态分布常记作。如果随机变量X服从正态分布，则记为。

在完成这一步之后，可以对德国数学家高斯（C.F.Gauss，1777-1855）与正态分布的渊源予以介绍，相关数学史内容的添加使得数学课堂更加丰满。

问题6 什么样的随机变量服从正态分布？

设计意图 数学源于生活，用于生活。通过对高尔顿板试验特点的分析，总结服从正态分布的随机变量的特点，使学生体会到数学给我们生活带来的巨大便利，数学建模素养能帮助我们理清思路、化繁为简。

4.3 小试牛刀，巩固所学

某地区数学考试的成绩服从正态分布，其密度函数曲线如图所示。

（1）指出和；

（2）计算的值；

（3）计算成绩位于区间的概率，即的值；

（4）计算的值；

（5）若，求的值；

（6）计算的值。

设计意图 通过具体问题的解决，进一步了解正态分布的特点，能够简单运用。

4.4 课堂小结，回顾感悟

（1）理解正态分布密度曲线和正态分布的特点，会简单运用正态分布解问题。

（2）对于生活中的实际问题，观察特点，建立数学模型，运用已学知识进行数量化分析，掌握分析问题的思路和方法，才能更加受益无穷。

5 教学反思

《正态分布》涉及知识点较多，如果不注重新知引入，将无法在学生现有水平下将概念本质渗透，学生脑海中所接收到的信息呈现出碎片化的特点，不利于理解及应用，而且不利于学生学习数学兴趣的培养。

本节课在知识考察上难度不大，在教学中应注重能力培养，而不仅仅是知识传授。数学建模素养能帮助我们剖析问题的特点，将实际问题数学化，利用数学的方法来分析问题。为促进学生对于知识的整体把握，还可补充与正态分布与二项分布之间的联系。

作者简介：王咪咪（1992.1—），女，陕西渭南，陕西师范大学数学与信息科学学院，2017级硕士，学科教学（数学）。