带式输送机断带捕捉器建模与动态仿真
2019-01-17白晓渊
白晓渊
(山西西山煤电股份有限公司太原选煤厂, 山西 太原 030023)
引言
带式输送机是煤炭行业煤炭生产过程用于煤炭运输的关键不可缺少的重要设备,但由于输送带的特殊工作特性及材料特性,在其长期、高负荷的工作状态下,会经常发生输送带断裂事故。断裂后失去控制的输送带及其上重物会向下滚落对两旁的行人、电缆、管路及其他设备等造成二次损坏。为了提高煤矿生产的安全性,带式输送机断带保护措施的研制必须得到相关方面的组织及机构的高度重视,当输送带断裂时断带捕捉器能及时、可靠地制动下滑的输送带,避免引发恶性事故。带式输送机断带捕捉器对输送带的制动特性除了依赖于断带捕捉器的自身结构特性外,更大程度上依赖于断带捕捉器在输送机系统上布置的结构形式,目前多数学者对输送机断带捕捉器抓捕特性的研究主要集中于断带捕捉器的本身,很少去对输送机系统上捕捉器的布置形式进行研究,因此本文以某型断带捕捉器为研究对象,通过对其进行建模和仿真分析,对不同布置结构下对其抓捕特性的影响进行了分析,对优化断带捕捉器的布置形式,提升输送机系统运行的安全性具有重要的指导意义。
1 断带捕捉器结构及工作原理
带式输送机断带捕捉器的机械结构组成及其安装位置如图1所示[1]。断带捕捉器的结构以及其工作原理决定了其在带式输送机上的特殊安装位置,一般来说,断带抓捕器拥有上下两块对夹式的闸块,安装时主要是将输送带处于两个闸块之间,由于输送带的特殊工作过程,需要在输送带的两侧同时各布置一套断带抓捕器,以保证抓捕力的平衡。断带抓捕器的作用主要是依靠上闸块的动作进行夹紧,上闸块主要通过与固定输送机在一起的液压缸提供动力。断带抓捕器发生断带抓捕行为时,上、下闸块都靠石棉制动摩擦片压住输送带,实现对断裂的输送带的可靠的制动。

图1 带式输送机断带捕捉器结构示意图
2 断带抓捕过程动力学模型的建立
利用离散元分析理论,建立带式输送机的简化数学模型,其结构如图2所示。图中:ki表示第i个离散单元的弹性系数,ci表示第i个离散单元的阻尼系数,mi为第i个离散单元的质量。
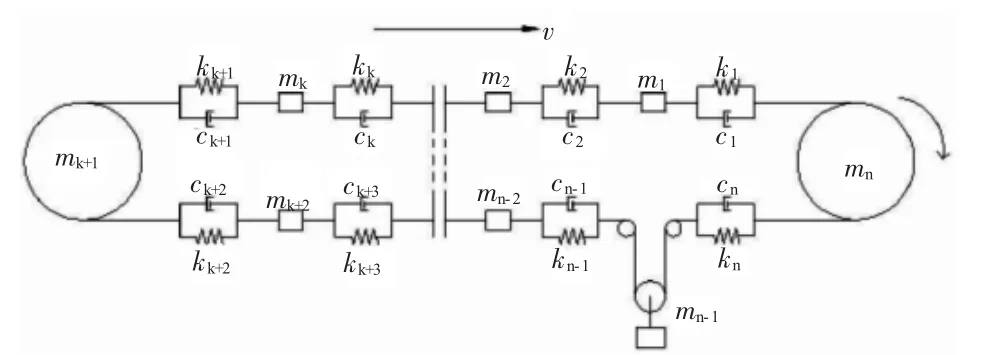
图2 带式输送机的离散元数学模型
如图2所示,将带式输送机系统的承载段划分为k个离散单元,将输送带的空载段划分为n-k-3个结构单元。
对第i个离散单元在制动时的受力情况进行分析,其受力如下页图3所示[2]。
由图3分析可知,第i个单元在制动时的受力方程可表示为[3]:

图3 第个离散单元的受力示意图

由于输送带的黏弹性特性,因此利用Vogit模型可分析得:

式中:Si为第i个离散单元上所受到的拉力;Si+1为第i+1个离散单元上所受到的拉力;mi为第i个离散单元的重量;mi+1第i+1个离散单元的重量;xi为第i个离散单元的位移;xi+1为第i+1个离散单元的位移;ki为第i个离散单元的弹性系数;ci为第i个离散单元的阻尼系数;fi为第i个离散单元制动时的摩擦力。
因此带式输送机系统输送带在断带抓捕器制动作用下的方程可表为:
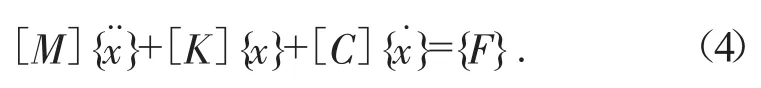
式中:{}为输送带的位移向量;{˙}为输送带的速度向量;{x}为输送带的加速度向量;[M]为输送带的质量矩阵;[K]为输送带的刚度矩阵;[C]为输送带的阻尼矩阵;{F}为外力向量。
3 制动时的动态仿真分析
将带式输送机划分为63个质量单元,其中承载段为30个质量单元,非承载区域的回程段划分为30个质量单元,将第37个质量单元定义为尾部改向滚筒,将第51个质量单元定义为张紧滚筒,将第63个质量单元定义为驱动滚筒单元,经计算该输送机系统中所需要的捕捉器的数量为31组,利用MATLAB软件将输送带在受制动情况下的动力学模型导入其中,采用的ODE解法进行求解[4],对不同抓捕器布置距离情况下输送带制动时的动态特性进行仿真分析。
3.1 等间距布置时的抓捕动态仿真
将31组捕捉器沿输送机机架均匀布置,因输送机下滑时重力越大,下滑时所需的制动力越大,因此本文对断带发生在输送机上侧机头位置处时的情况进行分析,结果如图4所示,图中1表示第3个质量单元的速度变化情况,2表示第17个质量单元的速度变化情况,3表示第30个质量单元的速度变化情况,速度大于零表示输送带向上运动,速度小于零表示输送带向下运动。

图4 等距离布置时不同质量单元的速度变化情况
由仿真分析结果可知,当断带事故发生后,输送带带速逐渐降低为零然后开始下滑,当断带捕捉器开始工作后逐渐实现对输送带的制动。其中第3个质量单元在约0.3 s时速度就降为零,其下滑时的最大速度约为3.39 m/s,第17个质量单元在约0.4 s时速度降低为零,其下滑时的最大速度约为2.83 m/s,第30个质量单元在约0.43 s时速度降低为零,其下滑时的最大速度约为3.57 m/s。当断带捕捉器开始制动后3号质量单元经过约2.71 s实现制动,第17个单元经过约2.49 s实现制动,第30个质量单元经过约2.14 s实现制动。由此可知,距离断点越近其速度下降的越快,执行抓捕时的制动时间也越长。
3.2 非等间距布置时的抓捕动态仿真
根据以上分析结果,对断带捕捉器设置时采取上密,下疏的布置方式,前10组设置为间距为20 m,第11—20组间距设置为30 m,第21—31组间距设置为40 m,其抓捕时的动态特性如图5所示。

图5 非等距离布置时不同质量单元的速度变化情况
由仿真分析结果可知,当断带捕捉器执行抓捕后,3号质量单元经过约2.2 s实现了制动,17号质量单元经过约2.5 s实现制动,第30个质量单元经过约2.52 s实现了制动,由于断带捕捉器在前部分布置密集,制动时的制动力较大,因此3号质量单元制动时的制动加速度最大,最先实现了制动。
通过对比断带捕捉器均匀分布和非均匀分布情况下,输送带制动时的动态特性,在采用非均匀分布情况下,断带捕捉装置制动时的制动力矩大、制动速度快,输送带下滑的距离小,而且根据实际验证其抓捕后输送带基本不会发生撕裂现象,因此在制动时所受的冲击最小,抓捕效果也最好。
4 结语
1)输送带断带后,距离断点越近质量单元的速度下降的越快,执行抓捕时的制动时间也越长。
2)采用捕捉器非均匀分布情况下,断带捕捉装置制动时的制动力矩大、制动速度快,输送带下滑的距离小,抓捕后输送带基本不会发生撕裂现象,因此在制动时所受的冲击最小,抓捕效果也最好。
