A cooperative spectrum sensing results transmission scheme with LT code based on energy efficiency priority

Song Xiaoqin Jin Hui Tan Yazhu Hu Jing Song Tiecheng

(1College of Electronic and Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China)(2 School of Information Science and Engineering, Southeast University, Nanjing 210096, China)

Abstract：To deal with a sharp increase in transmission energy consumption due to the presence of a large number of secondary users (SUs), an energy-efficient cooperative spectrum sensing results transmission scheme is proposed for cognitive radio systems. First, a cluster-based structure is introduced into the sensing results transmission scheme to reduce the transmission power. Then, the centralized sensing results transmission model is employed, and the non-fixed code rate Luby transform (LT) code is selected as the channel coding since its code rate can dynamically adapt to channel conditions and therefore avoid unnecessary redundancy in the transmission power. Furthermore, an improved optimal degree distribution (ODD) is designed for the LT code. The simulation results show that the choice of the appropriate parameters in degree distribution is very helpful for the LT code to achieve a promising performance. The ODD with optimized parameters can achieve more than 2 dB performance gain than other typical degree distributions when the bit error rate (BER) is 10-3. The energy consumption of the proposed scheme is not only at least 71.4% lower than that of the non-coding system, but also lower than that of the convolutional coding system with different code rates. Meanwhile, the energy consumption can be further reduced in the case that a suitable clustering method is selected.

Key words：cooperative spectrum sensing; energy-efficient; cluster-based; Luby transform (LT) code; degree distribution

Cognitive radio (CR)[1]has been widely investigated due to its promising capability in utilizing spectrum resources of fewer active systems. Spectrum sensing is one of the key technologies in CR networks. In order to detect the presence of primary users (PUs) more reliably, cooperative spectrum sensing[2]is introduced.

The channel diversity characteristics of the primary channels are studied in Ref.[3] for an opportunistic spectrum access according to channel quality to avoid collisions. In Ref.[4], an optimal wide-band spectrum algorithm is proposed, which enhances the performance of the secondary users (SUs) through joint detection of the PUs’ activities.

The primary target of the methods mentioned above is to maximize the transmission throughput. Thus, it is always assumed that the transmission power is large enough, which results in an increase in energy consumption, especially in the case of a relatively large number of cooperative SUs. However, with the background of advocating green communications[5], it is also necessary for terminals to optimize the energy consumption design to achieve a satisfactory user experience.

It is well-known that channel coding technology is always employed in a wireless system to guarantee the reliability of the data transmission. On the other hand, a well-designed channel coding can reduce the average transmit power per bit under a given bit error rate (BER) target. In conventional CR systems, channel coding is not used in spectrum sensing results transmission since the sensor results are assumed to be limited. However, with the increase of the cooperative spectrum sensing users and the sensing bandwidth, energy consumption in the transmission of sensing results cannot be ignored.

A reliable transmission of spectrum sensing data over different sensing nodes has become one of the focuses of research. Digital fountain[6]is a rateless channel coding which is considered to have achieved a balance between the energy-efficiency and the transmission reliability, and it is suitable for time-varying channels.

A practical implementation of fountain code is the LT code proposed by Luby[2]. The key factor to guarantee the operation of the LT code is the degree distribution in the encoding process. A good degree distribution should meet the following two requirements. First, the average encoding symbols should be as few as possible while ensuring the successful recovery of source symbols; secondly, the average degree of the encoding symbols should be as low as possible. In Ref.[7], the authors proposed a revised robust soliton distribution with only one parameter. The LT code with the revised distribution is implemented using the Kent chaotic map and pseudo-random sequence generator. However, in the case of high signal-to-noise ratio (SNR), the performance is relatively poor. Zhang et al.[8]proposed a method to design the degree distribution by combining several degree distribution schemes together. The proposed degree distribution takes advantages of several degree distributions and the optimal switching points are given. Ref.[9] shows that the LT code exhibits a high erasure floor due to poor minimum-distance properties, which can then be improved by maximizing the minimum variable-node degree in the decoding graph to reduce the transmission overhead. However, the computational complexity is too high to be applicable in sensing nodes. In Ref.[10], a new distributed LT code is proposed, which is especially suitable for the multiple access relay network with erasure channels. However, it is only employed in the special application scenario as it describes.

In this paper, the primary design target is energy efficient. Based on this consideration, a cluster-based cooperative sensing system structure is proposed to save energy during the transmission of sensing results. Meanwhile, an optimal degree distribution LT code is designed, which is effective both in theory and in practice.

1 System Model

1.1 Structure of the cluster-based cooperative sensing system

Cooperative spectrum sensing technology is proposed to improve the accuracy of spectrum sensing by utilizing multiple SUs to mitigate fading and shadowing effects.

Considering the energy efficiency, the cluster structure is used to transmit the spectrum sensing results, as shown in Fig.1. SUs are divided into different clusters according to their locations. SUs check whether the spectrum is used by PUs or not. Each selected SU in a cluster performs the spectrum sensing individually and sends sensing results to its cluster head (CH) . Each spectrum sensing result in SU is a binary hypothesis testing problem, whereH0means unused andH1means used.

Fig.1 Cluster-based cooperative sensing system

Each cluster has a CH. After receiving the sensing results from SUs in the same cluster, partial fusion decisions are made. The decision rule in each CH is the likelihood ratio. The likelihood functionP(y|H1) andP(y|H0) stands for the conditional probability of PUs using the spectrum or not, respectively. The PUs are considered to be present if the likelihood ratio meets

(1)

After obtaining the partial fusion decisions, CHs send the results to the fusion center. If a certain CH is far away from the fusion center, a relay is used to save energy. Otherwise, the CHs send their partial fusion decisions directly to the fusion center.

1.2 Centralized sensing information transmission model

Cooperative spectrum sensing can be either distributed or centralized. In Fig.2, the centralized approach is illustrated. After LT encoding and BPSK modulation, the sensing results of each sensing node in the same cluster are sent to CHs. Channel coding is employed to transmit the sensing results since it can balance the energy-efficiency and transmission reliability. The LT code is selected as the channel coding scheme since its encoding rate can adapt to channel conditions. The LT code executes coded bit mapping and is combined with the BPSK modulation. Then, the rateless code is transmitted through the AWGN channel. If the channel condition is getting worse, the encoding rate decreases correspondingly, and vice versa. Therefore, better energy efficiency can be achieved.

Fig.2 Centralized sensing information transmission system

The CHs demodulate the data and make local decisions, which is called partial fusion decisions. Then, the CHs encode the partial fusion decisions with the LT code and modulate the data again, and transmit them to the fusion center. Finally, the fusion center analyzes the received data to determine whether the PUs exist or not.

The main advantages of this cluster-based cooperative spectrum sensing lies in two aspects. On the one hand, only SUs with the highest SNR can be selected as the CHs. Therefore, the selective clustering gain can be obtained and the reliability of information transmission is improved. On the other hand, the number of all bits transmitted to the fusion center is significantly reduced since the transmission is carried out by CHs rather than by all SUs sensing nodes, and thus a low bandwidth control channel is easily formed. Since the performance of the LT code is related to the design of degree distribution, the principles of the LT code and several degree distribution schemes are described in Section 2.

2 Principle of LT Code and Conventional Degree Distribution Schemes

2.1 LT encoding and decoding

The LT encoder can generate encoded bits and generate potentially infinite bits. The decoder can recover the information bits from any set of the encoded bits, when the number of received bits is only slightly more than that of source bits[11-12].

2.1.1 Encoding ofthe LT code

In the LT encoder, each encoded bit is generated independently. Assume that the number of source bits in each group isKand the degree value isd.

The steps of generating encoded bits is as follows:

1) An integerdis chosen according to the output degree distribution.dis also called the degree of the output bits.

2) A set ofddistinct bits is chosen uniformly at random from theksource bits. Thedbits are called the neighbors of the encoded bits.

3) The encoded bits can be formed through the bitwise XOR operation of thesedneighbors.

An example of the LT encoding procedure is shown in Fig.3.

Fig.3 Schematic diagram of the LT encoding procedures

2.1.2 Decoding of LT codes

When decoding LT encoded packets, the belief propagation (BP) algorithm is an efficient low complexity algorithm. Using the BP decoder, some source packets can be decoded before all encoded packets are received. This is called the online decoding property of the LT code. The decoder first releases the encoded bits of degree-one, and the value of their unknown neighbors can be calculated by XOR operation. Then, the contribution of this encoded bits can be deleted to obtain a smaller graph. This process is repeated until there is no degree-one bits left. A decoding failure occurs when the decoder fails to recover all thekinformation bits. An example of the LT decoding procedure is shown in Fig.4.

Fig.4 Schematic diagram of the LT decoding procedures

2.2 Robust soliton distribution

(2)

(3)

μRSD(i) in robust soliton distribution (RSD) is given by the above two degree distributions as follows:

(4)

RSD is a universal design and it provides a convenient way for the degree distribution design.

2.3 Sparse degree distribution

In the sparse distribution function (SDD)[13-14], the degree distribution can be expressed as follows:

(5)

whereα(i) is the probabilities of the degrees, andα(1)=0.008,α(2)=0.494,α(3)=0.166,α(4)=0.073,α(5)=0.083,α(8)=0.056,α(9)=0.037,α(19)=0.056,α(65)=0.025,α(66)=0.003.

The complexity of the SDD is greatly reduced compared with that of RSD. Furthermore, the implementation of the SDD is relatively simple.

3 Optimal Degree Distribution Design

More efficient distribution has always been one of the hot issues in fountain codes research[15]. One characteristic of existing degree distribution schemes is that the probability of degree 1 is less than that of degree 2. This ensures that not too many redundant degree 1 packets are sent, leading to a more efficient transmission. However, it is well known that the ideal soliton distribution itself performs rather poorly, so the first two degree probabilities are selected as parameters.

(6)

whereδ1andδ2are the parameters obtained from the Monte Carlo simulation.

(7)

In the ODD, the allowable failure probabilityPfintroduced by Luby is removed since this parameter is only an approximation. In fact, the practical failure probability is much higher thanPf.

4 Performance Evaluation

In this section, the parameter selection and the performance of the ODD of the LT code are evaluated. Both the BER and energy efficiency are employed as the measures of the performance of the degree distribution schemes in the sensing results transmission.

4.1 The optimal values of parameters δ1 and δ2

The choice of the appropriate parameter values is very important for a promising performance of the degree distribution scheme. In Eq.(6),δ1andδ2are two important parameters. Tab.1 gives the simulation hypothesis to obtain the optimal parametersδ1andδ2by the Monte Carlo simulation.

Tab．1Simulation assumptions

ParameterValueSampling threshold0.1The maximum number of generated samples106Binary search interval[0,0.05]Binary search threshold0.000 1Maximum iterations15Simulation run times1 000Number of source bits per frame1 000Channel conditionAWGNModulation schemeBPSK

According to the Monte Carlo simulation results,δ1=0.079 andδ2=0.503 are obtained, which are then used in the ODD in the following simulations.

4.2 Impact of parameter c on the BER performance

In the simulations, each BER result is an average value of 1 000 frames, and the number of source bitsKin each frame is 252. The redundancy overhead is 0.4.

Fig.5 compares the BER of the LT code with different settings of parametercin ODD. From the results, ifcis smaller, the BER performance is better. However, the smallercincreases the complexity of the decoding. To achieve a balance between the performance and the complexity,c=0.1 is selected.

Fig.5 BER of LT code with different parameters c in ODD

4.3 BER performance with different numbers of source bits K in ODD

Fig.6 compares the BER performance of the LT code with the number of source bitsK=252 andK=504. From the result, when the BER is equal to 10-3, the required SNR in the case ofK=252 is about 1.1 dB larger than that ofK=504 case. Therefore, if the number of source bits is larger, the BER performance is better. If the number increases, the complexity also increases in both encoding and decoding. Therefore,K=504 is selected in the following simulation.

Fig.6 BER of LT code with different parameter K in ODD

4.4 BER of LT code with different degree distributions

Three different degree distribution schemes are simulated with the average redundancy overhead of 0.4,c=0.1 andK=504. The BER performance is illustrated in Fig.7. The ODD performs significantly better than the RSD and SDD. For the ODD, when the SNR is between 2 and 3 dB, the BER curve drops largely .

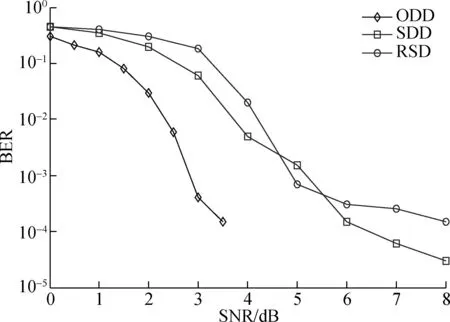
Fig.7 BER of LT code with different degree distributions

4.5 Performance of the ODD LT code vs. convolutional code in energy consumption

Comparing with other fixed code rate channel coding schemes, the LT code is more flexible. Its encoding redundancy overhead can adapt to the channel change. Here, the convolutional code is used as the typical example of fixed code rate channel coding for its lower code complexity. In this simulation, the constraint length is 3. Fig.8 gives the BER performance of the ODD LT code in Fig.7 and the convolutional code with the code rate of 2/3 and 1/2, respectively. A soft decision with 8 quantization levels is employed in the decoding of the convolutional code. It can be seen that the LT code outperforms the convolutional coding with 2/3 code rate, while it is worse than the convolutional code with 1/2 code rate.

Fig.8 BER of ODD with LT code vs. convolutional code

For the 2/3 rate convolutional code, the redundancy overhead is 0.5 and the required SNR is about 6.5 dB less than that of the non-code case at the target BER of 10-3. The energy consumption is about 33.6% compared with the non-code case, which means a saving of 66.4% of the total energy.

As to the 1/2 rate convolutional code, the redundancy overhead is 1 and the required SNR is about 7.5 dB less than that of the non-code case. The energy consumption is about 35.6% of the total energy.

Suppose that the redundancy overhead of the LT code with ODD is between 0.3 and 0.5. The energy consumption is about 24.8% to 28.6% of the total energy. Considering that the overhead of the LT code is 0.5 in the worst case, the LT code with ODD can save 71.4% energy consumption of the transmission than that of the non-coding case, which saves the energy of transmission spectrum sensing information greatly. The energy consumption comparison is shown in Tab.2.

Tab．2Comparison of energy consumption with a target BER of 10-3

Channel code schemeRedundancy overheadEnergy consumption/%Non-coding case0100LT code0.3 to 0.524.8 to 28.62/3 rate convolutional code0.533.61/2 rate convolutional code 135.6

4.6 Comparison of energy consumption with different clustering methods

Under the AWGN channel and the free space propagation model, it is assumed that the sensor nodes are uniformly distributed in the sensing range; the node number in each cluster is equal and the CH is in the center of each cluster. Take 20, 30 and 50 sensor nodes as examples and find the appropriate number of clusters.

Fig.9 illustrates the normalized energy consumption in different clustering assignment schemes. The number of sensing nodes in each cluster is supposed to be equal. In Fig.9(a), when the number of sensing nodes is 20, the minimum energy consumption is obtained by dividing the sensing nodes into 10 clusters and it is only 40% energy consumption compared with no clustering case. In Fig.9(b), when the number of sensing nodes is 30, the minimum energy consumption is obtained by dividing sensing nodes into 5 clusters and it is 34% energy consumption compared with no clustering case. In Fig.9(c), when the number of nodes in the cluster is 50, the minimum energy consumption is obtained by dividing the sensing nodes into 10 clusters and it is 27% energy consumption compared with no clustering case.

It is clear that the cluster-based system can significantly reduce the energy consumption. The more nodes that are included in the cooperative sensing system, the better the energy-saving results can be achieved if the appropriate number of clusters is selected.

(a)

(b)

(c)

5 Conclusions

1) The energy-efficient design for sensing results transmission is of great significance for cooperative spectrum sensing. The proposed scheme employs a cluster-based sensing system structure and the LT code channel coding to save energy.

2) An optimal degree distribution scheme is designed since the degree distribution can significantly influence the BER performance of the LT code. The BER performance of ODD is better than that of RSD or SDD. The degree distribution parameters and the number of source bits also have a significant impact on the BER performance. Considering the redundancy overhead of the LT code, the average energy consumption can be further reduced by optimizing the degree distribution design and selecting appropriate encoding parameters.

3) In view of the time-varying characteristic in the wireless channel, the rateless LT channel code contributes to energy saving. The typical fixed code rate channel coding system, i.e., the convolutional code, is simulated to prove that the proposed LT code is superior to the convolutional code channel coding scheme in terms of energy consumption. Meanwhile, the energy consumption of different clustering methods is compared, which shows that a suitable clustering method is also helpful for further reducing the energy consumption.