一类非线性单边值问题解的存在及一致衰减性
2019-01-16钟越,袁倩
钟 越,袁 倩
(成都文理学院,四川 成都 610101)
0 前言
本文讨论如下一类带非线性阻尼边界条件的波动系统
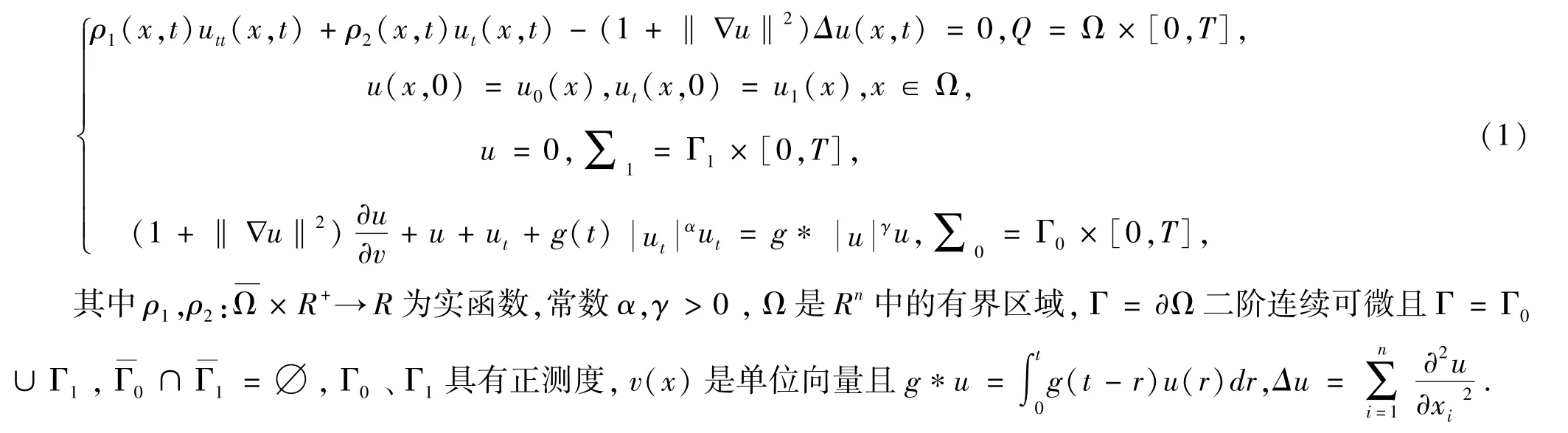
具有非线性边界条件的波动系统描述了弹性弦线的小振幅振动[2].近年来,带阻尼边界条件的基尔霍夫型波动系统解的存在及衰减出现在很多文献中.Jiang[4]和Georgiev[12]运用Faedo-Galerkin近似和扰动能量方法研究了两类系统的稳定性;Cavalcantietal等[7,9]则对带有记忆边界条件的基尔霍夫波动系统进行了讨论.Bae等[10]引入能量方程,研究了如下一类波动系统

其中‖∇u‖2=文献[10]利用Faedo-Galerkin近似方法得到了系统(2)解的存在性,同时运用扰动能量方法证明了(2)中解的一致衰减性.Yamada[1]研究了(2)中当∂Ω=Γ0,φ=1时的情形.另外,Matsuyama[3]运用相同方法讨论了当ε充分小时,如下初边值问题解的渐近性质

其中δ>0,0<ε≤1.此外,其他文献[5,6,8,11-16]研究了非线性边界条件下不同类型波动系统解的渐近性态.当α=γ时,系统(1)改写为
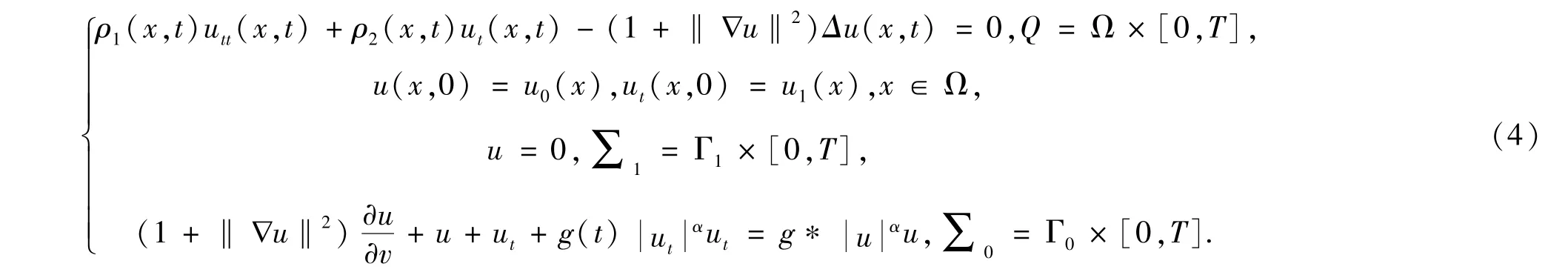
在初边值满足一定条件时,本文讨论波动系统(4)解的渐近性态.本文借鉴文献[3]和[10]的研究方法,在系统(4)解的存在唯一性及一致衰减性证明中使用了Faedo-Galerkin近似方法和扰动能量方法.
1 预备知识
定义[10]

当α=γ时,定义系统(4)的能量方程为

假设如下条件成立
(A1)设u0,u1∈V∩H2(Ω)满足
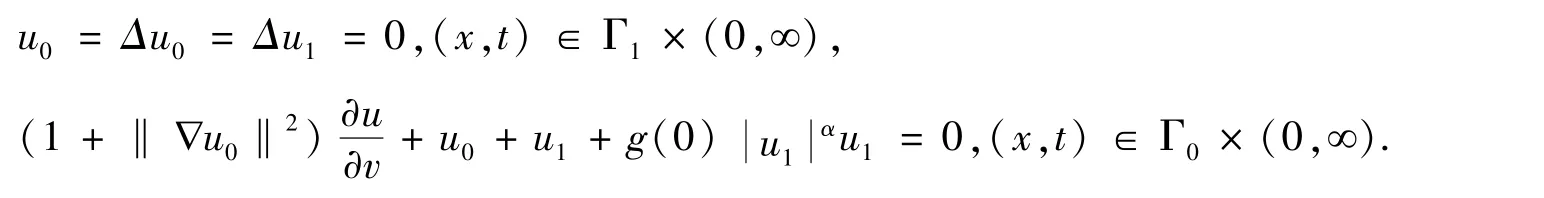
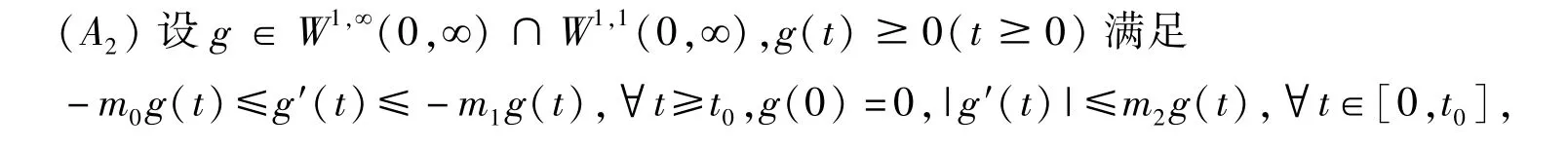
其中m0,m1,m2>0.
本文的主要结果如下
定理1.1若(A1),(A2)成立,则当α≥γ>0且

其中u′=ut,u″=utt.
定理1.2若(A1),(A2)成立,且

2 定理1.1的证明

取任意小的μ>0,由假设条件(A2),对任意不依赖于t的正数C0成立(1-μ)g(t)-μ‖g(t)‖L1(0,∞)<C0g(t)
在(0,t)上对(9)积分,由Gronwall引理可得如下估计


其中M2>0与m和ε无关.
运用Pirard叠代,在初边值条件下,系统(5)仅有唯一解存在于[0,Tm)中.由先验估计(10)及(13)可知系统(5)在[0,Tm)中的唯一解可扩展到[0,∞)上,定理得证.
3 定理1.2的证明




4 结论
本文讨论了一类带非线性阻尼边界条件的基尔霍夫型波动系统解的稳定性,给出了能量的衰减状态.在前人研究的基础上,本文将系统(4)中阻尼衰减项ut(x,t)的衰减系数由常数扩展为随时间和位移变化而变化的函数ρ2(x,t)形式.在函数阻尼系数条件下,系统能量的衰减不仅和时间有关,也会受到位移影响,但基本衰减方式仍然以指数形式衰减.这亦是本文工作与其他工作的不同之处.当然,也可将这种扩展运用于强迫阻尼系统中,如非齐次波动系统.
