广义混合变分不等式的有界性条件

罗雪萍

(西南民族大学计算机科学与技术学院，四川 成都 610041)

1 引言

变分不等式是的理论分析及应用近年来受到广泛关注，参见文献[1-15].作为变分不等式的重要推广，广义混合变分不等式引起众多学者的研究兴趣，并获得了大量的研究成果，参见文献[1-6].其中，广义混合变分不等式解集的性质是一个有趣的课题，引起了研究者们的广泛兴趣.关于广义混合变分不等式解集的有界性、闭性、连通性与连续性等均受到了关注，并涌现了许多相关的文献.

He[7]在自反巴拿赫空间中，讨论了广义变分不等式解集的有界性.Zhong与Huang[4]将文献[7]的有界性结果推广到f-伪单调的广义混合变分不等式的情形.其中，文献[4]中的有界性条件涉及到函数的回收函数.然而，研究发现利用共轭函数来刻画广义混合变分不等式的有界性条件较文献[4]中的条件会更弱.这样，一个新的有界性条件被论证是广义混合变分不等式具有非空有界解集的充要条件，同时还给出了具体例子支撑主要定理.

文章的结构如下：第二部分给出需用的概念及基础知识；第三部分在自反巴拿赫空间中，介绍广义混合变分不等式解集的有界性条件.第四部分证明了此有界性条件的充要性.第五部分总结全文.

2 预备知识

令X为自反巴拿赫空间且其对偶空间为X*，‖·‖为X中的范数，为X与X*的对偶对.设K为X中的非空闭凸集，F：K→2X*为具有非空值的集值映射，f：K→R∪{+∞}为真凸下半连续函数.将讨论以下广义混合变分不等式问题(简称为GMVI(F，K))，i.e.，求x∈K与x*∈F(x)使得

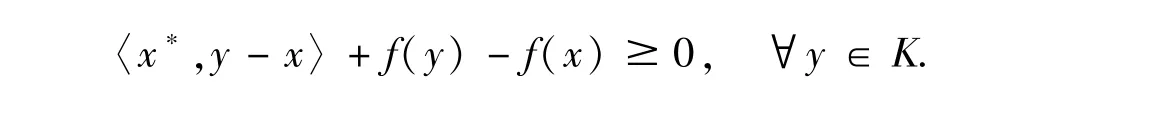
众所周知，与GMVI(F，K)紧密联系的对偶变分不等式，即Minty型混合变分不等(称为MMVI(F，K))，i.e.，求x∈K使得

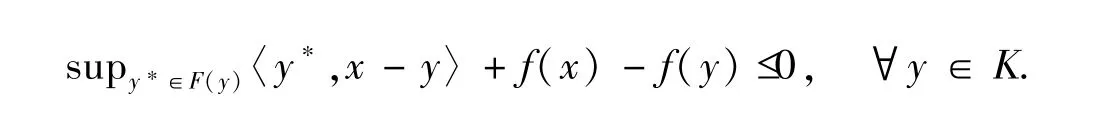
表示序列 {x}弱收敛到x.对于A⊂X，A的内部表示为intA.K的匣锥barrK被定义为

n barrK：={x*∈X*：supx∈K〈x*，x〉＜∞}.

K的回收锥K∞是闭凸锥，被定义为：

任意给定x0∈K，

K∞={d∈X：x0+λd∈K，∀λ＞0}.

令f：K→R∪{+∞}是真凸下半连续函数.f的回收函数f∞被定义为

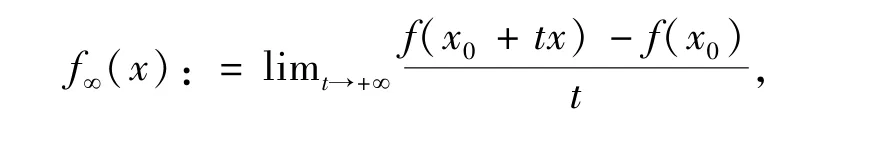
其中x0∈domf.因此，

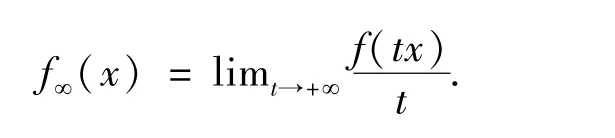
令：X*→R∪{+∞}被定义为

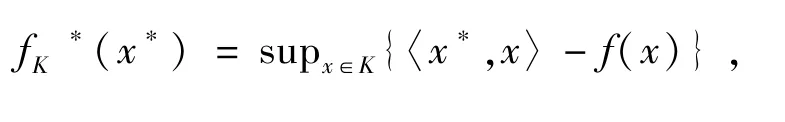
称为f的共轭函数.

K的指示函数IK被定义为

K的支撑函数σK：X*→R∪{+∞}被定义为

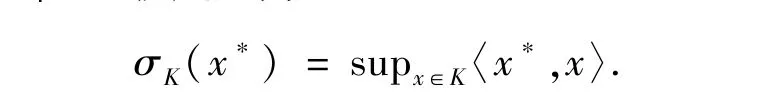
明显地，IK*=σK，domσK=barr(K).

定义1令F：K→2X*是具有非空值的集值映射，f：K→R∪{+∞}是函数.称F

(i)在K上单调，如果对于任意的x，y∈K及任意的x*∈F(x)，y*∈F(y)，

〈y*-x*，y-x〉 ≥0；

(ii)在K上伪单调，如果对于任意的x，y∈K及任意的x*∈F(x)，y*∈F(y)，〈x*，y-x〉≥0⇒〈y*，y-x〉 ≥0；

(iii)在K上f-伪单调，如果对于所有的x，y∈K及任意的x*∈F(x)，y*∈F(y)，〈x*，y-x〉+f(y)-f(x) ≥0⇒〈y*，y-x〉+f(y)-f(x) ≥0；

(iv)在x0∈K处上半连续，如果对于F(x0)的任意邻域N(F(x0))，存在x0的一个邻

域N(x0)，使得

(v)在K上沿线节上半连续，如果F在X*中关于弱拓扑在K中的任意线段都是上半

连续.

引理1[4，引理4.1]令K在中是非空闭凸集，F：K→2x*是非空值的集值映射，f：K→R∪{+∞}是凸函数.以下(i)与(ii)均成立：

(i)如果F在K上是f-伪单调，则GMVI(F，K)的任意解是MMVI(F，K)的解；

(ii)如果F在K上是沿线节上半连续，则MMVI(F，K)的任意解是GMVI(F，K)的解.

3 新的有界性条件

首先在自反巴拿赫空间中，给出一个新的广义混合变分不等式的有界性条件(W).假设K是X中的无界子集且int(barrK)≠∅，有

注释：如果f≡IK∞＼{0}，则≡σK∞＼{0}.由(1)，有

这样，存在∈F(K)，对于任意的x∈K∞＼{0}，有

即为，〈y0*，x〉＞0.因此，K∞∩F(K)-={0}，此式为广义变分不等式的有界性条件，被众多研究学者讨论，参见文献[7].

在文献[4]中的定理3.2给出了以下广义混合变分不等式有界性条件(S)并证明了其充分必要性.

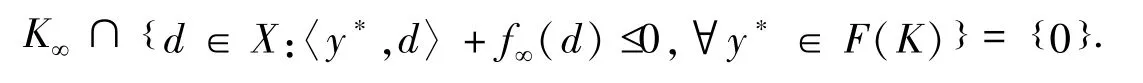
事实上，有界性条件(W)是弱于有界性条件(S)的.下面，将证实在自反巴拿赫空间中，有界性条件(W)是一个较弱的条件.

定理1令X是自反巴拿赫空间，K在X中是非空闭凸集，F：K→2x*是非空值的集值映射，f：K→R∪{+∞}是真凸下半连续函数.如果有界性条件(S)成立，则

证明：因为有界性条件(S)成立，所以对于任意的d∈K∞＼{0}，存在y0*∈F(K)，使得

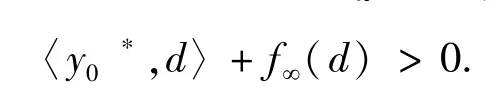
由f∞(·) 的定义可知

这样，对于足够大的t＞0，有

以下例子说明满足有界性条件(W)的广义混合变分不等式未必对有界性条件(S)成立.

例1令X=R，K=[0，+∞[.定义f：K→R为

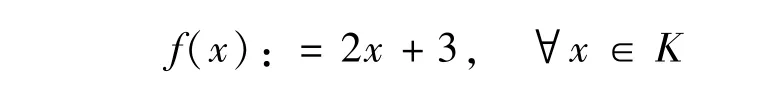
与F：K⇒R为

因此，对于所有的x∈R，K∞=K=[0，+∞[，

下面，将证实广义混合变分不等式满足有界性条件(W)，事实上，

然而，有界性条件(S)并不成立，

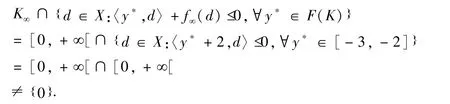
4 主要结果

第3节证明了有界性(W)是一个较弱的条件.鉴于文献[4]证明了有界性(S)是确保解集非空有界的充要条件，只需要证实(W)是确保广义混合变分不等式解集非空有界的充分条件即可.

定理2令K在X中是非空闭凸集且int(barrK)≠∅，F：K→2x*是沿线节上半连续与f-伪单调的非空值映射，f：K→R是真凸下半连续函数.如果有界性条件(W)成立，则GMVI(F，K)的解集非空有界.

证明：只需要证明存在有界集C⊂K，使得对于任意x∈K＼C，存在y∈C满足supy*∈F(y)〈y*，x-y〉+f(x)-f(y)＞0即可.若不然，类似文献[4]中定理3.2的证明，存在d∈K∞＼{0}使得

由f∞(·)的定义可知对任意的y*∈F(K)，有

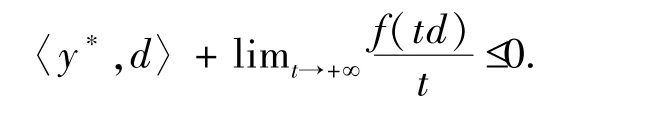
这样，对于足够大的t＞0，有

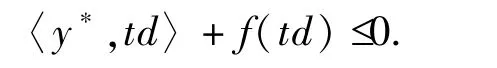
即为〈-y*，td〉-f(td)≥0.因为d∈K∞＼{0}和K∞是一个锥，td∈K∞＼{0}.对于任意的y*，存在d0=td∈K∞＼{0}，使得〈-y*，d0〉-f(d0)≥0.这样，与已知条件产生矛盾.类似文献[4]中定理3.2的证明，得到MMVI(F，K)的解集是非空有界的.然后，利用引理2.3即得证.证毕.

下面例子说明有界性条件(W)是广义混合变分不等式解集非空有界的充要条件.

例2令X=R，K=[0，+∞[.定义f：K→R为

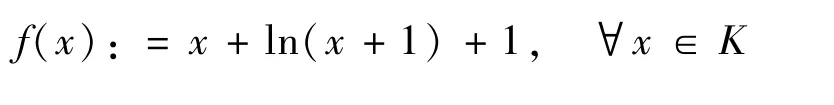
与F：K⇒R为

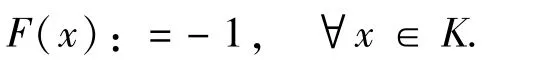
因此，对于所有的x∈R，K∞=K=[0，+∞[，

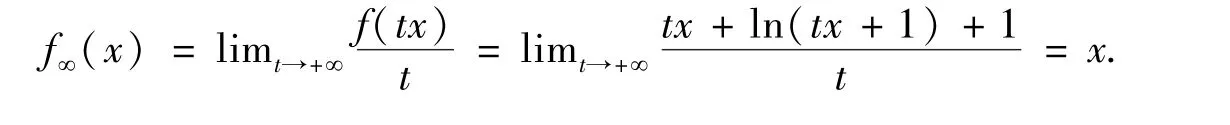
下面，将证实广义混合变分不等式满足有界性条件(W)，事实上，

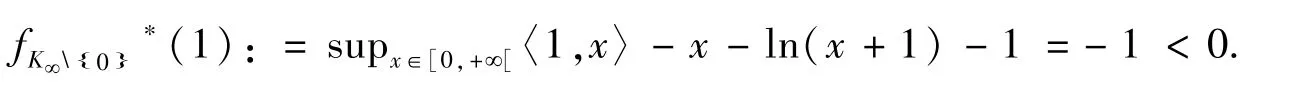
然而，有界性条件(S)并不成立，

通过简单的计算，可知此广义混合变分不等式解集是有界的单点集{0}.

5 结论

首次引入了广义混合变分不等式的一个新的有界性条件，并证明了此条件是确保解集非空有界的充分必要条件.最后，还给出了具体例子支撑主要定理.