太阳能光伏板阵列体型系数和最优展平角模拟

沈妍 王琪 康晓慷 谭强 卢晓聪

（1.江苏科技大学机电与动力工程学院 张家港215600；2.苏州聚晟太阳能科技股份有限公司 张家港215600）

引言

太阳能光伏板及其支架必须有一定的抗风能力。太阳能光伏板支架的设计中，风荷载是结构设计考虑的重要因素之一，风荷载的大小和分布直接影响支架的设计和材料选取。针对太阳能光伏板表面风荷载的精确估算，可避免盲目选型，对提高工程质量和支架寿命、节约成本有很大作用。

常用的太阳能光伏支架的设计规范有我国《建筑结构荷载规范（2012年版）》（GB 50009-2012）[1]、美国建筑结构荷载规范《Minimum Design Loads for Buildings and Other Structures（SEI／ASCE 7-10）》[2]、日本《太阳能光伏发电系统的设计与施工》[3]等，设计人员普遍认为我国《光伏发电站设计规范》（GB50797-2012）[4]中6.8.7条地面和楼顶光伏支架的体型系数取1.3过于保守，带来光伏产业支架成本的增加；同时，各国规范的取值标准不一，偏差较大，给设计参数的选取带来了困扰。此外，跟踪式光伏板系统在大风或夜间不工作时需要展平放置。为减小风压对结构稳定性的影响，可采用最优展平角放置。最优展平角是使太阳能光伏板的风压或体型系数最小的倾角，但最优展平角度设置和选取仍存有疑惑。

常用的研究方法主要有搭建试验台进行实际风洞测试[5]和利用CFD（计算流体力学）技术模拟风洞。越来越多的研究者依赖于较为成熟的CFD法进行模拟风洞，节约成本，适用性好，且通过比较，具有一定可靠性。吕宏伟等[6]、黄张裕[7]等通过分析和模拟对各国设计规范进行比较，给出了不同角度下体型系数取值建议。牛斌等[8]数值分析了各种强平均风或脉动风荷载对光伏板的影响，为光伏板的抗风性和强度设计选型提供依据。此外，研究人员还考虑了强平均风荷载下双列光伏板[9]、规则光伏板阵列[10]、不规则光伏板阵列[11]、屋顶光伏板[12]的体型系数，通过模拟和试验研究得到不同结构的体型系数。同时，还分析了倾斜角度、风向角、支架高度等因素对光伏板支架的影响[13]，并研究了阵列中板与板之间的遮挡效应[14，15]，研究的角度范围为0 ～90°，通常计算间隔为10°或15°，对于小倾角下最优展平角的相关研究还较少。此外，实际运行时通常是阵列分布，整排体型系数的分布规律还不甚清晰。

本文采用CFD方法分析软件CFX进行光伏板表面风压分布特性的数值计算分析，考虑小倾角工作情况下风荷载对光伏板的影响，找到体型系数最小的工作倾角即最优展平角。此外，光伏板阵列在多排布局时各光伏板排之间存在明显的遮挡效应，通过各排板的风压折减系数变化分析阵列各排受压的衰减程度，为工程应用提供依据。

1 流场的模拟

1.1 物理模型与参数

根据工程情况，本模型由8排太阳能板组成，每4排为一组，各排间距为4.5m，组间间距8m。每排布置7块光伏板，光伏板单板长1650mm，宽992mm，厚32mm。板与板之间留有间隙15mm。光伏板中心离地面高度1.2m。空间流体域取x方向90m，y方向10m，z方向12m，如图1所示。

太阳能光伏支架系统中广泛采用轻型钢或铝合金结构，重力影响相对较小，对风荷载比较敏感，尤其是受到恶劣天气的强风荷载或处于夜间非工作时间时，从安全和维护角度需要展平太阳能光伏板，以减小太阳能光伏板及其支架系统所受到的影响，此时为小倾角运行或展平运行工况，模拟中设置强风时工作倾角分别为0°、5°和10°，常用风速时工作倾角45°。

图1 太阳能光伏阵列模型Fig.1 Solar photovoltaic array model

阵列中，风向角为0°和180°时，风荷载作用于光伏板上的作用力较大；风向角为90°和270°时，风从侧向吹入光伏板，在光伏板上的作用力较小。因此，模拟工况分别考虑风向角为0°和180°，0°时产生的风压为正风压，180°时产生的风压为背风压。

1.2 理论与数学模型

计算流体力学的基本控制方程如下：

连续性方程：

运动方程：

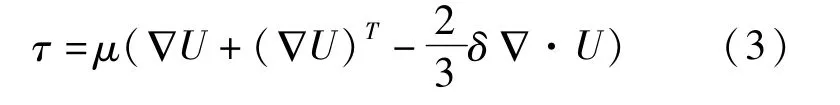
式中：ρ为密度，kg／m3；t为时间，s；U为速度矢量，m／s；p为压强，Pa；SM为动量源项；τ为切应力，N；μ为动力粘度，Pa·s；δ为克罗内克函数。

在工程中，光伏板处于低速风场中，可采用不可压缩粘性流体模型，且不考虑温度变化的影响，可认为流体的动力黏度和密度为常数。空气的物性参数，25℃1个标准大气压的空气动力粘度μ＝1.831 ×10-5Pa·s，密度ρ＝1.185kg／m3。湍流模型采用k-ε模型，差分格式采用高阶迎风格式，收敛残差设为1e-4。

将风压进行归一化处理，板表面点i的压力值为pi，表面参考静压为p0，两者之差与来流风的速度压之比，即为点i处的平均风压系数Cpi：

体型系数等于风压系数除以风压高度变化系数。根据荷载规范，低于10m的B类地貌高度系数为1.0，因此计算后得到的风压系数等于体型系数。

入口设置为速度边界条件。45°时为常用工作工况，取正常运行风速18m／s。0°、5°和10°为强风时展平工况，取强风风速33m／s。光伏板所受风速为：

式中：Zr为参考高度；vr为参考高度下的参考风速；α为地面粗糙指数。

图2 光伏板受正风压时上表面和下表面的压强Fig.2 The pressure of the upper and lower surfaces of the photovoltaic panels under positive wind

图3 光伏板受背风压时上表面和下表面的压强Fig.3 Pressure of the upper and lower surfaces of the photovoltaic panels under leeward pressure

风荷载的设计来流风速条件为：A类场地指数率剖面，地面粗糙指数α为0.12。对应的Zr为10m，该高度处风速vr为42.5m／s，则电池面板中心1.2m高度处的风速为33m／s。

出口面设置为自由出流边界条件。两侧和顶侧设置为对称边界条件。底面设置无滑移壁面边界条件。光伏板设置为无滑移壁面边界条件。

2 计算结果和分析

2.1 各排板平均压强随倾角的变化

1.正风压

正风压时，太阳能光伏板不同倾角下各排上表面和下表面的平均压强如图2所示。正风压时上表面均受到正压，下表面均受到负压。10°倾角时风压最大，5°倾角和45°倾角时风压次之，0°倾角时风压最小。因此，0°～10°倾角时，同等风速下倾角越大，风压越大。

上表面，45°倾角时，风压在第2排骤减，倾角较大时正风压上表面的遮挡效果明显。第3排至第8排的风压和5°倾角时相差较小。这是因为45°倾角的流速较小，与5°流速33m／s工况的风压相近。

5°倾角和10°倾角的风压变化规律相似，第1排风压最大，第2排至第4排风压逐渐减小；由于第4排和第5排之间间距较大，第5排的风压有所上升，随后第6排至第8排的风压逐渐减小。随着倾角的增大，第2排折减效果越明显。间距增大，折减效果变差。正风压下表面的遮蔽情况受倾角的影响较上表面小。

2.背风压

背风压时，太阳能光伏板不同倾角下各排上表面和下表面的平均压强如图3所示。背风压时上表面均受到负压。10°倾角时，光伏板上受到的负压最大，5°倾角时受到的负压次之，0°倾角的风压最小。

0°时，第一块板的迎风端，气流撞击板侧，产生较大的压强，但在上下表面的压强接近0Pa，流线平行着流过光伏板，板上所受压强最小。

3.上下表面共同作用

受到上下表面的正负压综合作用，每排板的平均压强变化如图4所示。10°倾角33m／s受到的风压最大，5°倾角33m／s时次之，45°倾角18m／s时再次之，0°倾角33m／s时最小，因此，最优展平角为0°即平行于风向角放置。

图4 光伏板各排的平均风压Fig.4 Average wind pressure of each row of photovoltaic panels

2.2 各排板体型系数随倾角的变化

前文进行了光伏板各排表面的平均风压比较，但风压数值受风速影响很大，为了减小风速的影响，分析倾角的影响，采用体型系数进行比较。

图5 光伏板受正风压时上表面和下表面的体型系数Fig.5 Shape coefficient of upper and lower surfaces when photovoltaic panels under positive wind pressure

图6 光伏板受背风压时上表面和下表面的体型系数Fig.6 Shape coefficient of the upper and lower surfaces of the photovoltaic panels under leeward pressure

1.正风压

正风压时，太阳能光伏板不同倾角下各排上表面和下表面的体型系数如图5所示。下表面的体型系数大于上表面。

倾角和排间距影响体型系数的变化。上表面，45°倾角18m／s时第1排的体型系数最大，第2排骤减，第3排又略上升，前5排波动较大，随后趋于平稳。下表面，45°倾角时的体型系数第1排最大，第2排骤减，最后逐渐增大。10°、5°和0°倾角时的体型系数变化较45°倾角时较小。因此，大倾角时，行间距的影响较大。10°倾角和5°倾角的变化规律相似，其中第1排的体型系数最大，第2排至第4排逐渐递减；由于第4排和第5排间距较大，第5排的体型系数较第4排略增，随后逐排略减趋于平稳。0°倾角的体型系数最小。

2.背风压

背风压时，太阳能光伏板不同倾角下各排上表面和下表面的体型系数如图6所示。背风压下表面为迎风面受正压，体型系数为正值；上表面为背风面受负压，体型系数为负值。

45°倾角的体型系数波动较大。45°倾角时，第1排的体型系数绝对值较大。第2排体型系数最小，遮挡效果明显。第2、3、4排受到第1排的遮蔽，第6排受到第5排的遮蔽。10°倾角的体型系数绝对值最大，其次为5°倾角，再次为0°倾角，和正风压时规律一致。

3.上下表面共同作用

受到上下表面的正负压综合作用，每排板的体型系数变化如图7所示。上下表面共同作用后体型系数明显增大。45°倾角的体型系数最大，10°倾角时次之，5°倾角时再次之，0°倾角时最小。本文10°倾角的计算值在文献[16]中实验值之间。

本文体型系数的计算值与文献的计算值、实验值比较如图8所示。在0°～10°范围内，本文计算值比文献[5]实验值和文献[7]计算值相比略大。体型系数的影响因素有板尺寸、倾斜角度、排列间距等。文献[5]实验值和文献[7]计算值的研究对象为单板，板的长宽尺寸对体型系数有一定的影响，单板试验值和计算值结果较小，多板阵列计算结果较大。此外，文献[7]中提出对于倾角0°～15°的光伏面板，体型系数可取仰角为15°时的值，正风压取0.755，背风压取-0.95，与本文计算值相近。小角度工况的研究常常被忽略，本文的结果可为工程应用提供一定的参考。

图7 各排光伏板的体型系数Fig.7 Shape coefficient of each row of photovoltaic panels

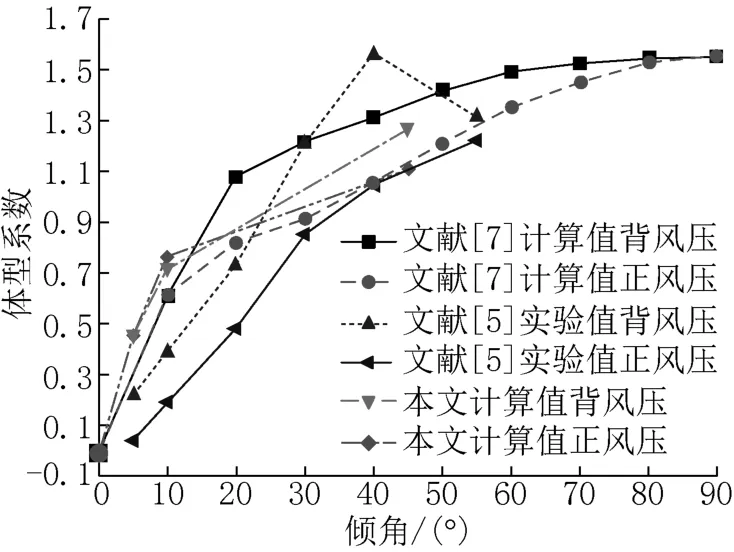
图8 体型系数计算值与文献的计算值、实验值比较Fig.8 Comparison of calculated values of shape coefficient with calculated and experimental values from literatures

2.3 各排板折减系数随倾角的变化

折减系数定义为本排体型系数与前排体型系数的比值。因此，第1排无折减系数。折减系数越小，遮蔽效果越好。不同倾角下，各排折减系数如图9所示。5°、10°和45°倾角时，在第1组光伏板中，受到第1排的遮挡，第2排折减系数最小。第2组光伏板中，受到第5排的遮挡，第6排折减系数最小。组与组之间间距较大时，每组的第一排遮蔽效果较差，如第5排的折减系数较大，每组的第1排对第2排有较好的遮挡效果。文献[8]中25°倾角背风压的第2排折减系数为13%，本文45°倾角背风压的第2排折减系数为14.6%，可供太阳能光伏板运行时对比参考。

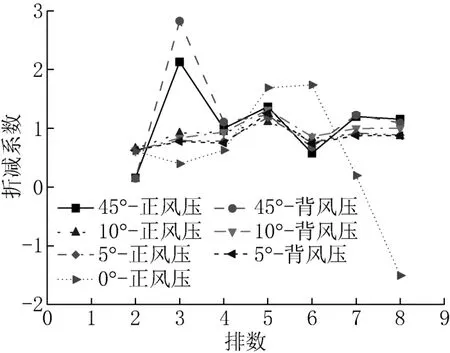
图9 光伏板各排折减系数Fig.9 Reduction factors of photovoltaic panel row

45°倾角时折减系数波动较大，10°和5°的折减系数变化较小，0°倾角的折减系数变化无规律。因此，折减系数受倾角的影响，大倾角各排之间的遮蔽效果明显。

3 结论

本文考虑了0°、5°、10°和45°倾角、18m／s和33m／s风速、4.5m和8m排间距对风压和体型系数的影响，通过数值计算得到以下结论：

1.在0°和180°风向角即正风压和负风压时，0°、5°和10°倾角中，0°倾角为最优展平角，板上下表面所受风压或体型系数最小，即板平行于风向时的倾角为风压或体型系数最小的最优展平角。相同风速下，倾角越大，风压越大。

2.倾斜放置时正风压和背风压下各排所受风压存在折减，每组光伏板受到第1排的遮挡，第2排折减系数最小。组间距较大时，每组第一排的体型系数较大，第一排对第二排有较好的遮挡作用。