波形钢腹板数量对组合箱梁抗扭性能的影响研究

2019-01-15唐杨唐卫国田俊国

特种结构 2018年6期

唐杨唐卫国田俊国

（1.重庆交通大学土木工程学院 400074；2.国网湖北省电力有限公司五峰县供电公司宜昌443413）

引言

随着20世纪80年代法国建成世界上第一座波形钢腹板预应力混凝土组合箱梁桥开始，波形钢腹板组合箱梁桥逐渐进入专家学者的视野。德国、委内瑞拉、挪威、日本等一些国家都相继开始了波形钢腹板组合箱梁桥的研究和建造。尤其是日本在20世纪末引入波形钢腹板组合箱梁桥之后，到目前为止，已经建成此类桥型200余座。目前看来，波形钢腹板组合箱梁桥具有经济、美观、受力合理、施工简便的特点，是一种可以广泛推广的桥梁结构，我国对于此类桥型的设计与研究起步较晚，近些年随着一些桥梁专家的研究和推广，截止2013年我国也修建了20余座波形钢腹板组合箱梁桥[1]，其中已经修建的波形钢腹板组合箱梁桥以单箱单室结构居多，单箱多室结构较少。现今为了满足日益增长的交通量，桥面宽度逐渐增加，单箱多室结构的波形钢腹板组合箱梁桥也逐渐进入更多专家学者的视野，比如2008年竣工的青海三道河桥为单箱双室结构，2009年竣工的郭守敬桥、钢铁路桥、梁庄路桥、邢州路桥为单箱七室结构，2010竣工的卫河大桥为单箱三室结构[2]。

波形钢腹板组合箱梁由于采用波形钢腹板代替了混凝土腹板，截面的抗扭刚度下降较多，在偏心荷载作用下扭转效应较为明显，而目前对于波形钢腹板组合箱梁抗扭性能的研究主要针对单箱单室波形钢腹板组合箱梁结构[3-5]，其中对于抗扭性能的影响参数研究主要针对波形钢腹板的板厚、倾角、水平段长度、横隔板数量及布置、内衬混凝土以及混凝土板厚等[6，7]。单箱多室波形钢腹板组合箱梁的研究目前主要针对腹板剪应力[8]、剪力滞效应[9，10]、内衬混凝土布置方式[11]、横向受力[12]以及动力特性[13]，而抗扭性能方面的研究很少涉及。总的来看，单箱多室波形钢腹板组合箱梁的抗扭性能有待专家学者的进一步研究和探索。

本文将针对单箱多室波形钢腹板组合箱梁抗扭性能的研究现状，首先以波形钢腹板的数量为唯一变量，根据规范建立理论分析模型研究波形钢腹板的数量对组合箱梁抗扭性能的影响，然后以卫河大桥为工程背景，研究两腹板布置与四腹板布置在实桥中对组合箱梁抗扭性能的影响，最终通过理论模型和实桥模型综合分析结果，得出波形钢腹板的数量对结构抗扭性能的影响程度。

1 建立分析模型

1.1 理论分析模型

根据薄壁杆件结构力学中的扭转理论，箱梁在偏心荷载作用下会造成结构的扭转，偏心荷载作用下，结构会产生附加的扭转正应力和扭转挠度。在波形钢腹板组合箱梁的扭转计算中，将偏心荷载分解为一个对称荷载和一个反对称荷载，依据力的叠加原理，通过计算偏心荷载和对称荷载作用下结构的正应力和挠度，可以得到偏心荷载作用下结构的扭转正应力和扭转挠度，即反对称荷载作用下的扭转效应。

为了简化理论分析的难度，这里仅仅建立一个简单的波形钢腹板简支箱梁。不考虑波形钢腹板以外其他结构参数对抗扭性能的影响，波形钢腹板的数量为模型中的唯一变量。同时，为了在模型中保证变量的唯一性，在模型中没有建立横隔板和预应力钢束。

首先建立一个只有边腹板的单箱单室波形钢腹板简支箱梁，其结构参数均参照《公路波形钢腹板预应力混凝土箱梁桥设计规范》（DB41／T 643-2010）拟定，结构参数具体设置为箱梁顶板宽11m，底板宽7m，梁高5.5m，箱梁长48m，计算跨径47m，顶板厚40cm，底板厚60cm，波形钢腹板的结构参数直接取用规范中的1600型波形钢板。单箱单室波形钢腹板简支箱梁截面尺寸如图1所示。上、下混凝土板考虑为C60混凝土，波形钢腹板考虑为Q345钢。然后在图1所示的单箱单室波形钢腹板简支箱梁的边腹板之间插入波形钢腹板，分别插入1、2和3块波形钢腹板，每个对比模型中分别保证波形钢腹板之间的距离为等间距，这样就形成了3块腹板（单箱双室）、4块腹板（单箱三室）、5块腹板（单箱四室）的波形钢腹板简支箱梁结构，在第2节中将对比腹板总量为2块腹板、3块腹板、4块腹板、5块腹板的波形钢腹板组合箱梁的抗扭性能。

采用Midas FEA建立理论分析的有限元模型，上、下混凝土板采用3D实体单元建模，波形钢腹板采用2D板单元建模，采用印刻功能将混凝土板和波形钢腹板的节点耦合，支座位置设置节点单元，节点单元施加简支梁约束，节点单元与支座范围内的混凝土底板表面节点刚性连接，其中5块腹板的波形钢腹板简支箱梁结构有限元模型如图2所示。

图1 简支箱梁横截面尺寸（单位：cm）Fig.1 Cross-sectional dimension of simple box girder（unit：cm）

计算荷载考虑为跨中集中荷载和全桥均布荷载两种，同时分别考虑两种荷载的对称布置与偏心布置。为了避免应力集中，集中荷载考虑为顶板上2m×2m的均布面压力，对称加载时面压力为P1＝P2＝0.1MPa，偏心加载时面压力为P2＝0.2MPa，P1＝0。将集中荷载换算成相同荷载总量的均布荷载施加在全桥，均布荷载考虑为顶板上2m×48m的均布面压力，对称加载时面压力为Q1＝Q2＝0.00417MPa，偏心加载时面压力为Q2＝0.00834MPa，Q1＝0，荷载横向布置如图3a所示。集中荷载考虑为跨中纵向2m长的范围内加载，均布荷载考虑为全桥纵向48m长的范围加载，荷载纵向布置如图3b和图3c所示。

计算分析中以箱梁的四个角点为对象提取偏心荷载和对称荷载作用下的正应力和挠度，顶板角点为1和2，底板角点为3和4，如图3a所示。

1.2 实桥分析模型

以大广高速公路冀豫界至南乐段的卫河大桥为工程背景，卫河大桥为47m+52m+47m的单箱三室波形钢腹板连续箱梁桥，卫河大桥边跨立面如图4a所示，中跨立面如图4b所示。箱梁截面的顶板宽16.85m，底板宽11.85m，翼缘悬长2.5m，箱梁梁高3.2m，顶板厚25cm，底板厚22cm，横截面如图5a所示。为了在实桥上研究腹板对箱梁抗扭性能的影响，建立对比模型，对比模型中混凝土翼板和波形钢腹板的结构参数均不变，仅仅将原来卫河大桥的两块中腹板去掉，其横截面如图5b所示。

图3 荷载布置（单位：cm）Fig.3 Load layout（unit：cm）

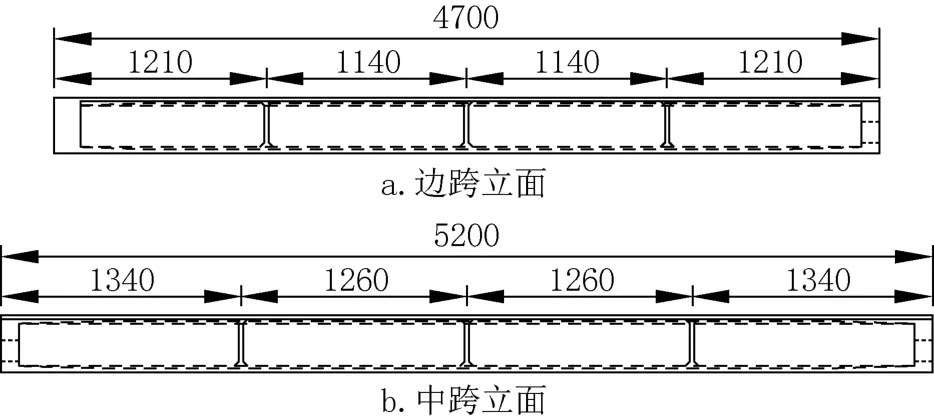
图4 卫河大桥立面布置（单位：cm）Fig.4 Facade of Weihe Bridge （Unit：cm）

卫河大桥混凝土板采用C50混凝土，弹性模量34500MPa，泊松比0.2，容重γ＝ 25kN／m3。波形钢腹板采用规范中的1200型波形钢板，波形钢板厚度设置为12mm，采用Q345qc钢材，弹性模量206GPa，泊松比0.3，容重γ＝76.98kN／m3。体内束和体外束钢绞线的抗拉强度标准值为1860MPa，公称直径15.2mm，弹性模量195GPa，泊松比0.3，容重γ＝78.5kN／m3。

分别在卫河大桥的模型上施加偏心汽车荷载和对称汽车荷载，对称汽车荷载横桥向布置见图6a，偏心汽车荷载横桥向布置见图6b。

图5 横截面尺寸（单位：cm）Fig.5 Cross-sectional dimensions （unit：cm）

图6 汽车荷载布置（单位：cm）Fig.6 Automotive load layout（unit：cm）

纵桥向汽车荷载布置见图6c。汽车荷载采用公路-Ⅰ级荷载，集中荷载施加于中跨跨中纵向2m宽的车道面上，集中荷载为PK＝360kN，均布荷载为QK＝10.5kN／m，均换算成面压力施加。

卫河大桥同样采用Midas FEA建立实桥有限元模型，建模中将混凝土板采用3D实体单元建模，波形钢腹板采用2D板单元建模，采用面面交线的方法建立三维体内预应力钢束，利用程序内置的植入式钢筋梁单元建模，不考虑体内预应力钢束与混凝土之间的滑移。体外预应力钢束采用桁架单元建模，采用预应力功能施加体外预应力荷载，采用印刻节点和内部线的功能将体外预应力与混凝土横隔板锚固的地方共节点连接。不考虑波形钢腹板与上、下混凝土翼板的滑移，采用印刻功能将混凝土翼板与波形钢腹板共节点连接，横隔板与上、下混凝土翼板共节点连接。卫河大桥的实桥有限元模型见图7。在模型中忽略了卫河大桥梁中心线与河道的85°交角，考虑为正桥建立模型，同时忽略横隔板的具体细节尺寸，将横隔板作为20cm厚度的等厚度板考虑，忽略横隔板与波形钢腹板的焊钉连接。卫河大桥中同样以4个角点为研究对象进行扭转效应分析，角点布置如图6a和图6b所示。

图7 卫河大桥有限元模型Fig.7 Finite element model of Weihe Bridge

荷载上考虑自重，自重荷载因子Z＝-1；考虑体内预应力钢束的预应力损失，松弛系数0.3，预应力钢筋与管道壁的摩擦系数0.3，管道每米局部偏差的摩擦影响系数0.0066，锚具变形和每端钢筋回缩6mm；同时施加桥面对称荷载及偏心荷载研究波形钢腹板组合箱梁的扭转。边界上，在箱梁底板印刻出真实的支座范围，在支座范围的中心建立节点添加一般支承约束，采用连接单元内的刚性连接将中心节点与支座范围内的节点连接，避免支座位置反力过大造成应力集中。

2 抗扭性能理论分析

通过计算对称集中荷载、偏心集中荷载、对称均布荷载、偏心均布荷载作用下的主梁正应力和主梁挠度，即可计算得到偏心荷载作用下的扭转正应力与扭转挠度。偏心荷载作用下的扭转正应力和扭转挠度计算方法为：扭转正应力等于偏心荷载作用下的正应力减去对称荷载作用下的正应力，扭转挠度等于偏心荷载作用下的挠度减去对称荷载作用下的挠度。

首先计算出对称荷载作用下和偏心荷载作用下的正应力和挠度，提取纵桥向13个截面的顶板2号角点和底板4号角点结果数据，然后计算出顶板2号角点和底板4号角点的扭转正应力以及顶板2号点的扭转挠度。下面对1.1节中建立的理论模型进行扭转分析，将偏心集中荷载作用下的扭转效应和偏心均布荷载作用下的扭转效应分别进行计算。

2.1 偏心集中荷载作用

按照1.1节中所示在跨中施加偏心集中荷载和对称集中荷载，计算得到偏心集中荷载作用下的顶板2号角点和底板4号角点的扭转正应力，如图8所示。

由图8a可以看出，在跨中偏心集中荷载作用下，随着波形钢腹板数量的增加，顶板的扭转正应力没有明显变化，仅在跨中位置可以看出随着波形钢腹板数量的增加，扭转正应力呈现减小的趋势。在跨中截面，波形钢腹板的数量从2块增加到5块，顶板扭转正应力最大值下降0.15MPa，下降幅度为14.1%。由图8b可以看出，底板的扭转正应力变化趋势与顶板相似，波形钢腹板的数量从2块增加到5块，底板扭转正应力最大值下降0.16MPa，下降幅度为19.3%。

按照1.1节中所示在跨中施加偏心集中荷载和对称集中荷载，计算得到偏心集中荷载作用下的顶板2号角点的扭转挠度，如图9所示。

图8 偏心集中荷载作用下扭转正应力Fig.8 Torsional normal stress under eccentric concentrated load

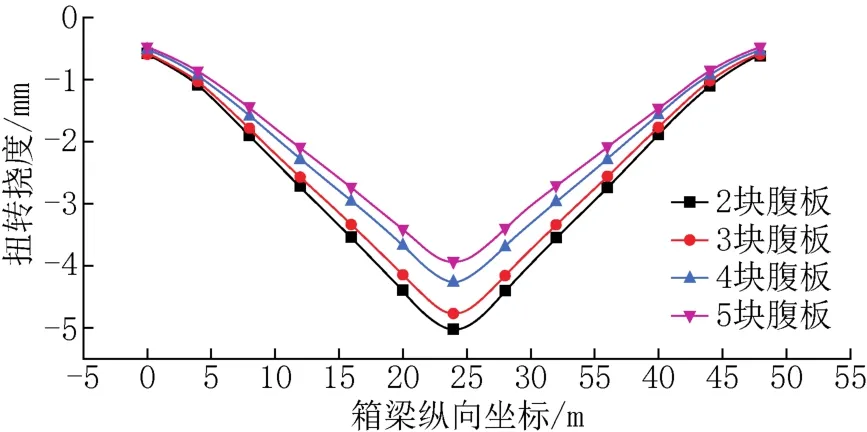
图9 集中荷载作用下扭转挠度Fig.9 Torsion deflection under concentrated load

由图9可以看出，波形钢腹板数量越多其扭转挠度越低，波形钢腹板的数量从2块增加到5块，扭转挠度最大值下降0.61mm，降低幅度为22.8%。

总的来看，在跨中偏心集中荷载作用下，增加波形钢腹板的数量可以在一定程度上增强箱梁的抗扭性能。

2.2 偏心均布荷载作用

按照1.1节中所示施加偏心均布荷载和对称均布荷载，计算得到偏心均布荷载作用下的顶板2号角点和底板4号角点的扭转正应力，如图10所示。

由图10a可以看出，偏心均布荷载作用下，随着波形钢腹板数量的增加，顶板的扭转正应力下降，波形钢腹板的数量从2块增加到5块，扭转正应力最大值降低0.04MPa，降低幅度为18.2%。由图10b可以看出，偏心均布荷载作用下，随着波形钢腹板数量的增加，底板的扭转正应力下降，波形钢腹板的数量从2块增加到5块，扭转正应力最大值降低0.07MPa，降低幅度为21.2%。

图10 偏心均布荷载作用下扭转正应力Fig.10 Torsional normal stress under uniform load

按照1.1节中所示施加偏心均布荷载和对称均布荷载，计算得到偏心均布荷载作用下的顶板2号角点的扭转挠度，如图11所示。

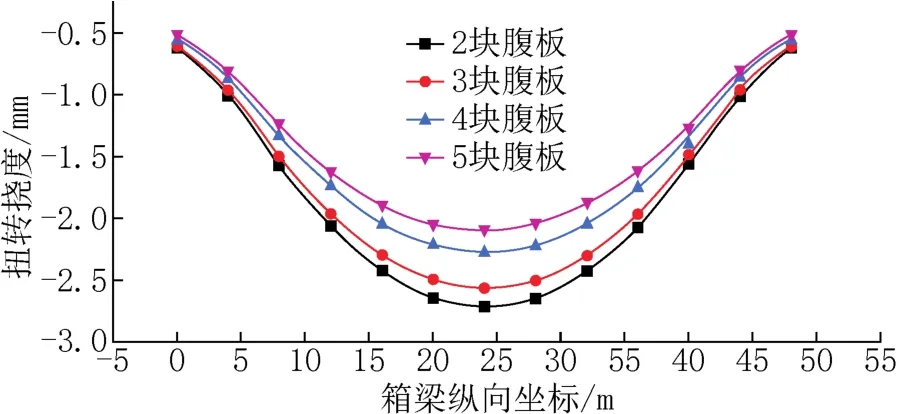
图11 均布荷载作用下扭转挠度Fig.11 Torsional deflection under uniform load

由图11可以看出，波形钢腹板数量越多其扭转挠度越低，在跨中位置，波形钢腹板的数量从2块增加到5块，扭转挠度降低1.09mm，降低幅度为21.7%。

总的来看，在偏心均布荷载作用下，增加波形钢腹板的数量会增强箱梁的抗扭性能，与偏心集中荷载作用下类似，在跨中位置，波形钢腹板的数量从2块增加到5块，扭转挠度和扭转正应力的下降值都在20%左右。

3 抗扭性能实桥分析

通过计算四腹板模型和两腹板模型在汽车偏心荷载作用和汽车对称荷载作用下各截面的正应力和挠度，得到两模型各截面四个角点的扭转正应力和扭转挠度，如图12所示。

图12 扭转效应对比Fig.12 Comparison of torsional effects

由图12a可以看出，在偏心汽车荷载作用下，扭转正应力的最大值出现在中跨跨中，四块腹板模型的扭转正应力最大值为0.33MPa，两块腹板模型的扭转正应力最大值为0.44MPa。四块腹板的模型相比于两块腹板的模型，扭转正应力最大值下降了0.11MPa，下降幅度为25.0%。由图12b可以看出，四块腹板模型的扭转挠度最大值为2.04mm，两块腹板模型的扭转挠度最大值为1.82mm，二者相差不大。

根据以上实桥分析可以看出，波形钢腹板的增加，降低了扭转正应力，但在扭转挠度的降低上表现不太明显。综合扭转正应力和扭转挠度的计算结果来看，在实际桥梁结构中，增加波形钢腹板的数量可以在一定程度上提高波形钢腹板组合箱梁的抗扭性能。