电磁式柔性直线驱动器概念设计与参数优化

刘海涛，魏天元，王友渔，刘玉华



电磁式柔性直线驱动器概念设计与参数优化

刘海涛1，魏天元1，王友渔2，刘玉华1

(1.天津大学机构理论与装备设计教育部重点实验室，天津 300350；2.北京空间飞行器总体设计部，北京 100094)

设计了一种结构紧凑可实现力位解耦控制的电磁式柔性直线驱动器．该柔性驱动器主要由变刚度装置和位置调节装置两部分组成，其中变刚度装置采用双线圈-永磁铁对称布置结构，通过动态改变线圈中输入电流的大小调节电磁力，从而实现变刚度输出．建立了通电线圈周边磁场的数学模型，并采用等效磁荷法推导出永磁铁在通电线圈磁场中所受电磁力的显示表达式．在此基础上，分析了设计参数对电磁力的影响规律，完成了变刚度装置的参数优化设计．通过虚拟仿真分析了变刚度装置的力-位移和力-电流特性，并将实验结果与理论结果进行对比，验证了变刚度装置力-位移和力-电流特性的准确性和有效性．结果表明，所设计的柔性直线驱动器能够实现变刚度控制．

电磁式柔性驱动器；概念设计；优化

传统的刚性驱动器在工业机器人中被普遍使用，具有轨迹跟踪效果好、高带宽和高精度等特性，但因其动态负载适应能力差，故不适于人机交互的作业环境[1]．为满足非确定性动态环境的作业需求，柔性驱动器成为新兴的研究热点[2]．柔性驱动器(或称弹性驱动器)是一种将传统刚性驱动元件和弹性机构组合而成的驱动装置[3]，根据其刚度可调性可分为定刚度柔性驱动器和变刚度柔性驱动器两类．其中，变刚度柔性驱动器因具有适应负载变化能力强、人机交互顺应性好[2]等优点成为柔性驱动器的主要发展方向．

变刚度柔性驱动器可根据工况实时调节输出刚度[2,4]，其中机械式调节的方式最为常用．机械式调节方法的原理是：通过改变内置弹性元件的预紧力或预加负载实现驱动器的刚度调节．此类变刚度柔性驱动器的常见结构形式可分为弹簧串联配置和拮抗配置两类，VS-Joint[5]和VSA-II柔性驱动器[6]是其典型代表．此外，通过改变输出构件和弹性单元的位置也可实现驱动器的变刚度调节[7]，如HVSA[8]和AwAS[9]柔性驱动器通过控制弹簧的位置改变输出刚度，vsaUT[10]柔性驱动器则通过调整负载位置实现刚度控制，而AwAS-II[11]和vsaUT-II[12]柔性驱动器通过调整杠杆转轴实现刚度调节．另外，机械式刚度调节还可以通过改变弹性单元的有效长度实现．例如，Jack Spring柔性驱动器通过增加或减少弹簧的有效圈数实现输出刚度的调整[13]，Choi等[14]和Tao等[15]设计的变刚度机器人关节通过控制与板簧相连的滑块位置改变板簧的有效长度，实现关节的变刚度．应当指出的是，上述柔性驱动器需要配置独立的伺服电机及相应的机构调整输出刚度，如滚珠丝杠机构[11,15]、行星齿轮系[8,12]和四杆机构[15]等，使得柔性驱动器结构复杂、响应速度慢．采用具有变刚度特性的新型材料是实现刚度调节的另一种方法[16-18]，如铁磁性材料、压电陶瓷、形状记忆合金等．此类柔性驱动器具有结构简单、体积小、输出力大等优点，但因存在迟滞、非线性、蠕变等问题，导致控制困难．

值得注意的是，目前研究中所提出的柔性驱动器多应用于仿生机器人[2-4]，而仿生机器人关节几乎均为转动副驱动，因而对适用于移动副驱动的柔性直线驱动器研究较少．基于以上分析，本文提出一种结构紧凑、响应速度快、可实现变刚度控制的电磁式柔性直线驱动器．建立了柔性直线驱动器的电磁力数学模型，完成了结构设计、参数优化、力-位移与力-电流特性分析，验证了设计方案的可行性．

1 概念设计

现有的柔性直线驱动器体积较大，如何通过作动原理创新，设计出结构紧凑的柔性直线驱动器是本文的研究重点．本文所提出的电磁式柔性直线驱动器的结构如图1所示，主要由位置调节装置和变刚度装置两部分组成．位置调节装置包括伺服电机、联轴器、丝杠螺母、导轨滑块、轴承及轴承滑动套；变刚度装置包括线圈、永磁铁、直线轴承及输出杆．丝杠、输出杆、线圈及永磁铁采用同轴布置形式，线圈固定在变刚度装置的基座上，永磁铁与输出杆刚性连接，且两端安装有复位弹簧，线圈断电时可提供回复力，保证永磁铁处于平衡位置．变刚度装置安装在滑块上，由丝杠带动实现直线移动．其工作原理为：永磁铁在通电线圈内部受磁场作用产生电磁力，通过改变输入电流实现对电磁合力的调整，经输出杆与负载力平衡，从而实现变刚度调节和输出力控制．该柔性直线驱动器结构紧凑，原理简单，可实现力位解耦控制，简化了控制方法，同时采用电磁作动原理具有响应速度快的特点．

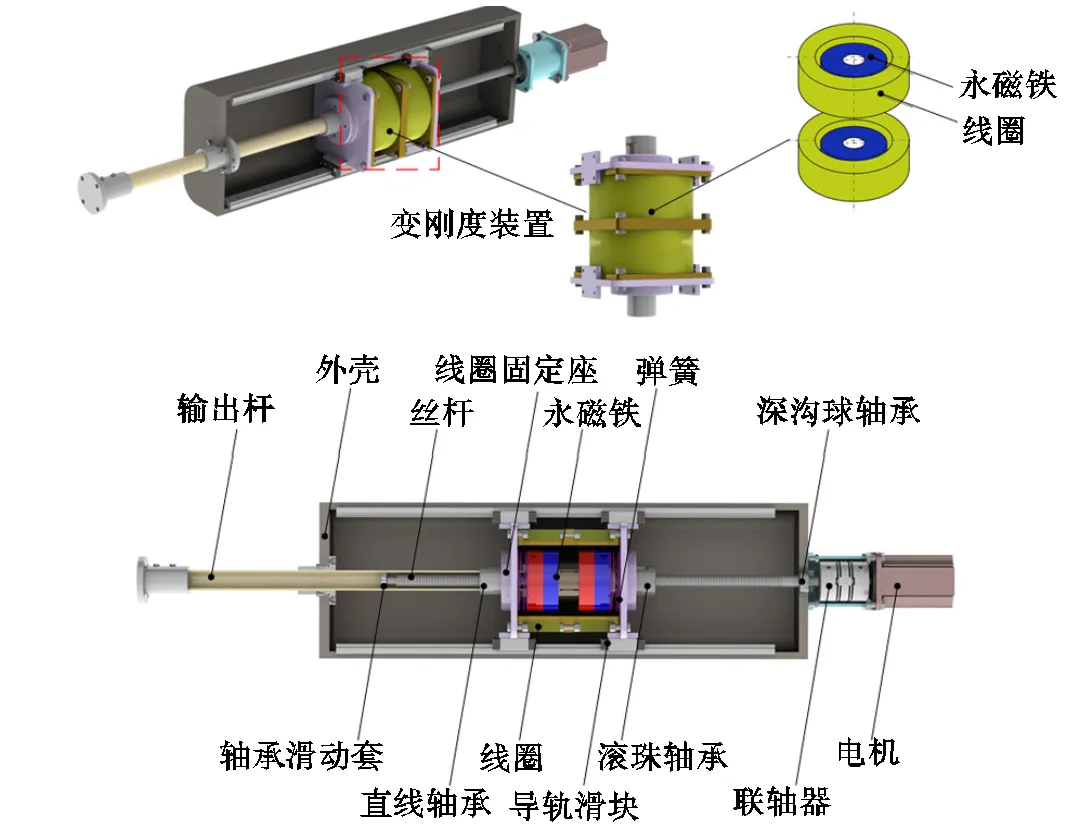
图1 柔性驱动器三维模型

2 数学模型

变刚度装置是该电磁式柔性直线驱动器的核心单元．为开展柔性驱动器参数优化设计及特性分析，首先需要建立永磁铁在通电线圈磁场中所受电磁力的数学模型．图2所示为变刚度装置的原理，两侧通电线圈和永磁铁采用对称布置方式，由于通电线圈中心位置的磁场分布相对均匀且稳定，将两个永磁铁分别布置在通电线圈的中心位置．永磁铁A和B在通电线圈1和2产生的磁场中所受的合力即为变刚度装置的输出力．注意到磁场强度为矢量，故多个通电线圈在空间任一点产生的总磁场强度可表示为各通电线圈在该点处磁场强度的矢量叠加(见图2受力分析)，因此可将两个永磁铁所受的合力0简化表示为

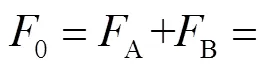
     (1)

式中：A1和A2分别为通电线圈1和2产生的磁场对永磁铁A的作用力；B1和B2分别为通电线圈1和2产生的磁场对永磁铁B的作用力；AB为永磁铁B对永磁铁A的作用力；BA为AB的反作用力．

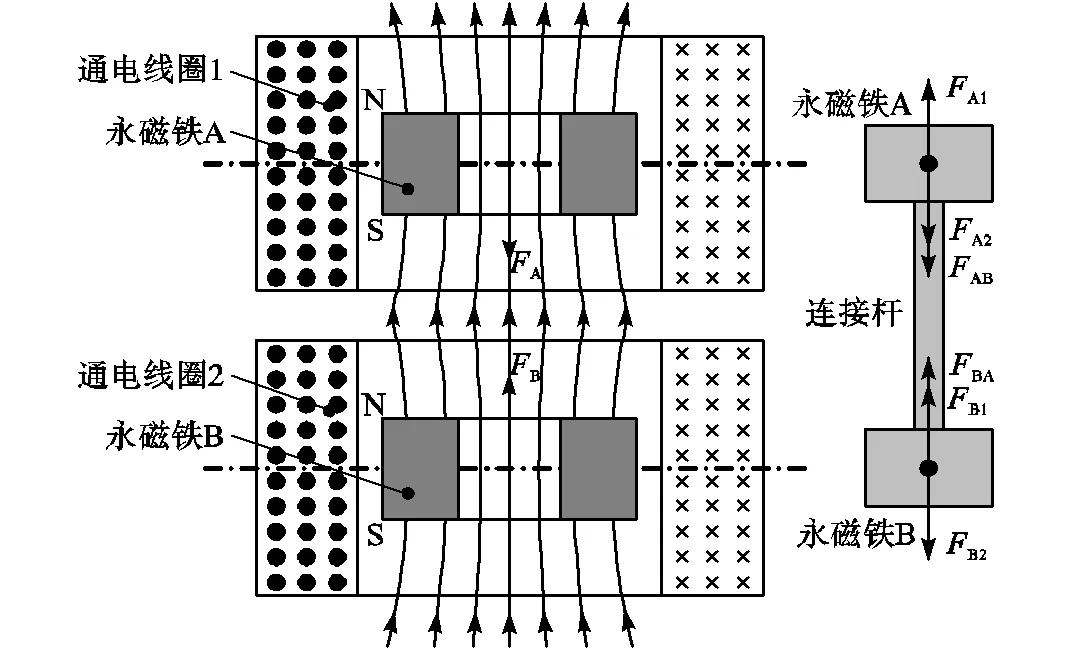
图2 变刚度装置的原理示意

由电磁理论可知，有限长度通电线圈内部产生的磁场沿其轴线方向呈非均匀分布，越靠近通电线圈的中间位置，磁感线越密集．根据等效磁荷理论[19]，永磁铁在磁场中所受的磁力是其两个磁极端面(简称极面)所受电磁力之和．因两个永磁铁置于通电线圈内部的中心位置，而内部磁场在中心位置两侧呈对称分布，故两个极面受到的电磁力大小相等、方向相反，即A1、B2均为零．此外，由于永磁铁A、B刚性连接，两者之间的作用力相互抵消，故式(1)可化简为

   (2)

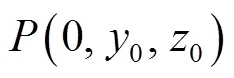
   (3)

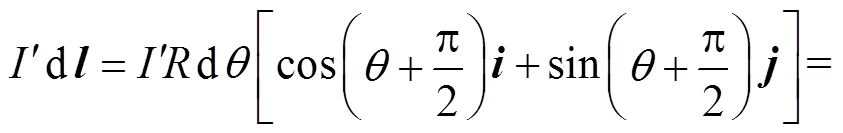
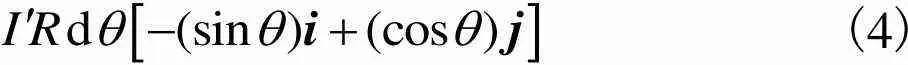
     (4)

式中和分别表示、轴的单位矢量．

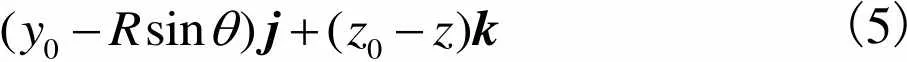
     (5)

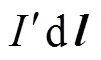
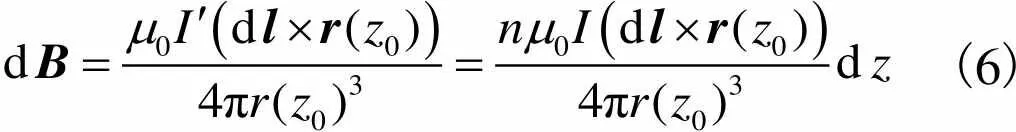
   (6)

根据等效磁荷法，永磁铁极面所受的电磁力仅与极面法向磁感应强度有关，因此只需求出方向的磁感应强度dB，故

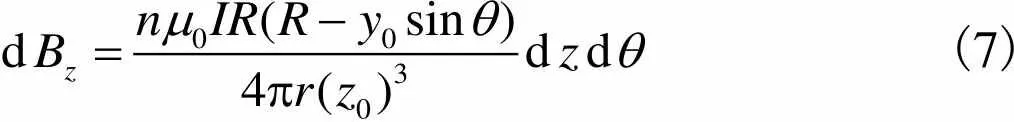
   (7)

对式(7)进行二重积分，可得单层通电线圈在点磁感应强度的方向分量

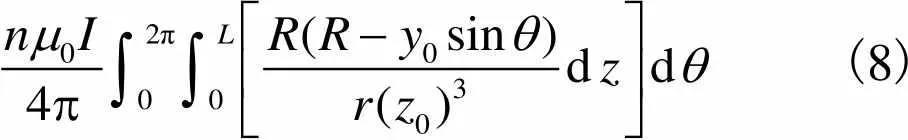
     (8)

对式(8)再次积分可得多层通电线圈在点磁感应强度的方向分量

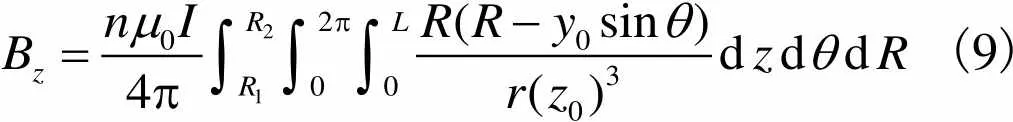
   (9)

式中：1为线圈内径；2为线圈外径．

通电线圈1与永磁铁B间相互作用力的理论模型如图4所示，永磁铁B的端面磁荷在通电线圈1的磁场中所受的磁力为

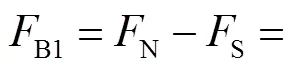
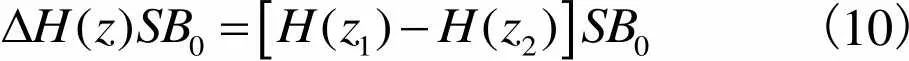
     (10)

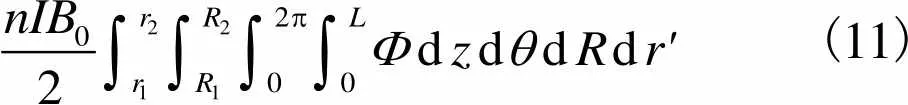
     (11)

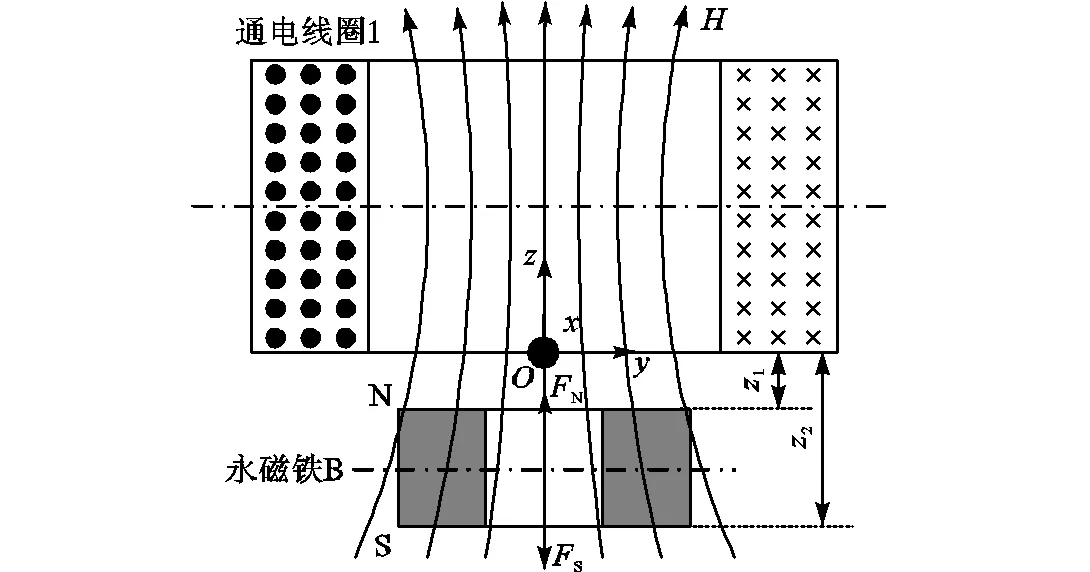
图4 变刚度装置简化模型

式(11)同样适用于永磁铁A的相关计算．由于两对通电线圈和永磁铁受力原理以及尺寸参数完全相同，可将式(2)写为

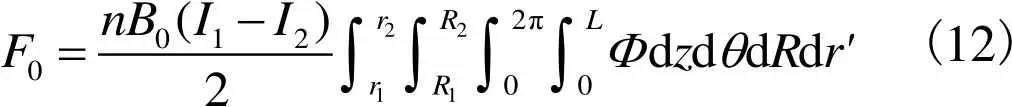
   (12)

式中1和2分别为通电线圈1和2的电流．由式(12)可知，两个永磁铁所受合力与两线圈通入电流的差值呈线性关系，当线圈1和2通入同向等大电流时，永磁铁A和B受到大小相等、方向相反的电磁力，变刚度装置处于平衡位置．当线圈1和线圈2通入同向但大小不等或反向电流时，永磁铁A和B所受电磁力的合力不能相互抵消，即可实现柔性驱动器的变刚度控制．

3 参数设计

根据该柔性驱动器的设计原理，通电线圈和永磁铁的尺寸及其相对位置关系对变刚度输出具有重要影响，因此利用所建立的受力模型进行设计参数优化．基于体积小、质量轻、结构紧凑、便于加工、经济可靠等基本设计原则，位置调节装置拟选用半径6mm的滚珠丝杠，且考虑到滚珠丝杠与永磁铁之间的预留间隙，设定永磁铁的内径110mm；为保证柔性驱动器结构紧凑，设定线圈的外径2＝50mm；同时避免永磁铁与线圈发生干涉，设定两者间隙＝5mm．各参数定义参见图5．除上述设定的边界条件外，其余设计变量为线圈高度1、厚度2、线圈距中间对称位置距离3、永磁铁高度4．由于两个永磁铁的受力规律完全一致，仅分析单个永磁铁的受力规律即可，注意到单个永磁铁所受的电磁力受多个参数影响，需利用式(11)分析出其受力规律，并找出该永磁铁所受最大电磁力对应的参数取值，确定为最优设计参数．因此，该柔性驱动器的优化设计可转化为下述优化模型，即

   (13)

表1 优化模型的参数

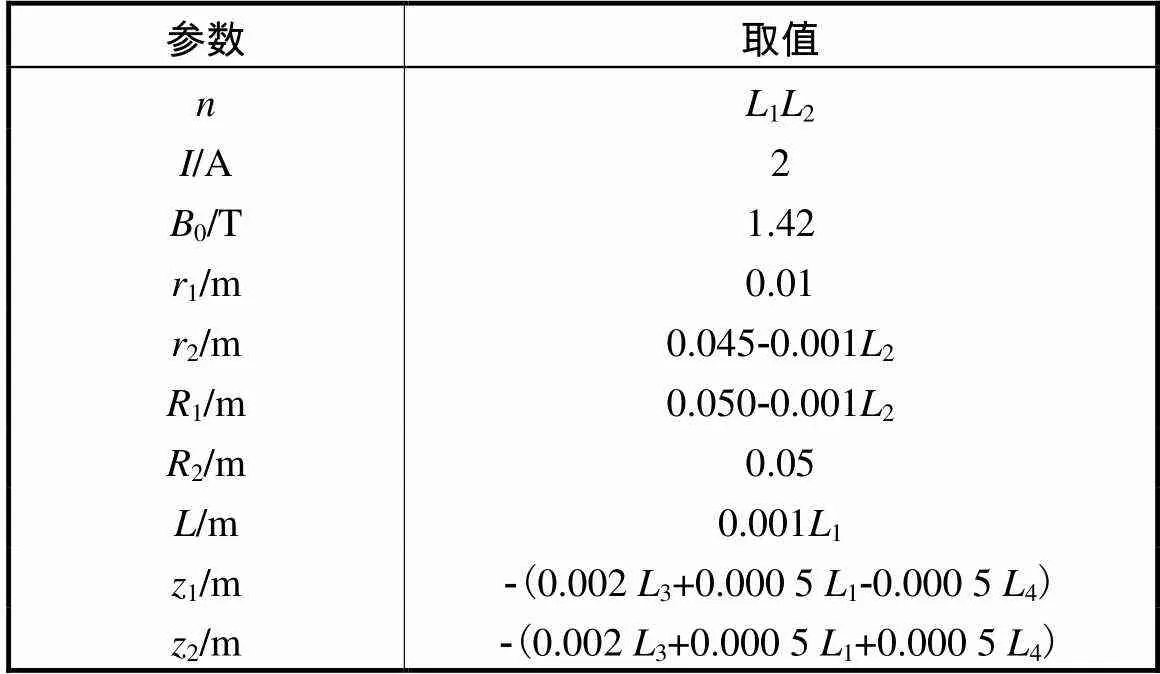
Tab.1 Parameters of the optimization model

本文采用图谱分析的方法确定最优设计参数，主要方法为绘制在给定区间内所有优化变量所对应的电磁力变化曲线，并在所有变量组合中确定电磁力最大值所对应的一组变量组合作为最终优化结果．因此需要求解单个永磁铁所受电磁力随变量1、2、3、4变化的曲线图．首先应确定各变量的分析区间，考虑到已设定的边界条件和精简计算的原则，设定变量的范围及取值步长如表2所示．将4个设计变量1、2、3、4以及表1中各参数的代数式代入优化模型(式(13))，得到只含设计变量1、2、3、4的数学表达式．利用MATLAB绘制随变量1、2、3、4变化的曲线图．由于无法直接描绘随各变量的变化曲线，分析时先将永磁铁所受电磁力作为纵坐标，设计变量1作为横坐标，其他设计变量每次取分析区间内的固定值并遍历全部组合，绘制出随变量1变化的特性曲线，如图6(a)所示，同理分别绘出随其余设计变量变化的曲线图(见图6)．由图6可知，永磁铁所受电磁力随1、3、43个变量的变化曲线均表现出单调性，在设计变量分析区间的边界取得极值；而随2的增加先增大后减小，在中间取得极值．因此，1、3、4的最优解为1＝40mm，3＝5mm，4＝30mm．

通过上述分析可将式(13)的优化问题转化为关于2的单变量搜索问题．图7给出了变量1、3、4取最优值时，随变量2的变化规律，当2＝15mm时，该永磁铁所受电磁力取得最大值．

表2 设计变量的范围及取值步长

Tab.2 Range and step size of design variables

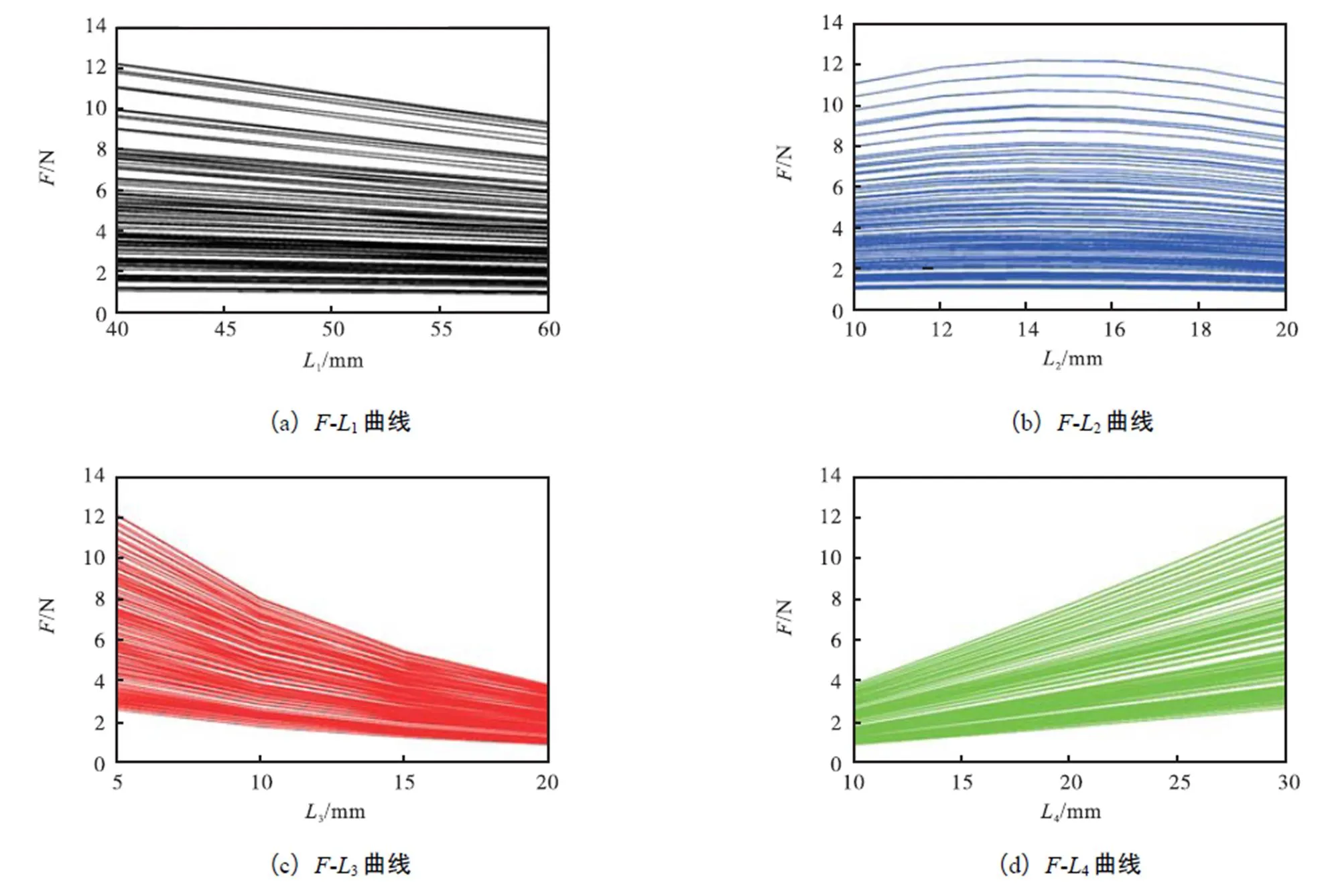
图6 F随L1、L2、L3、L4的变化曲线

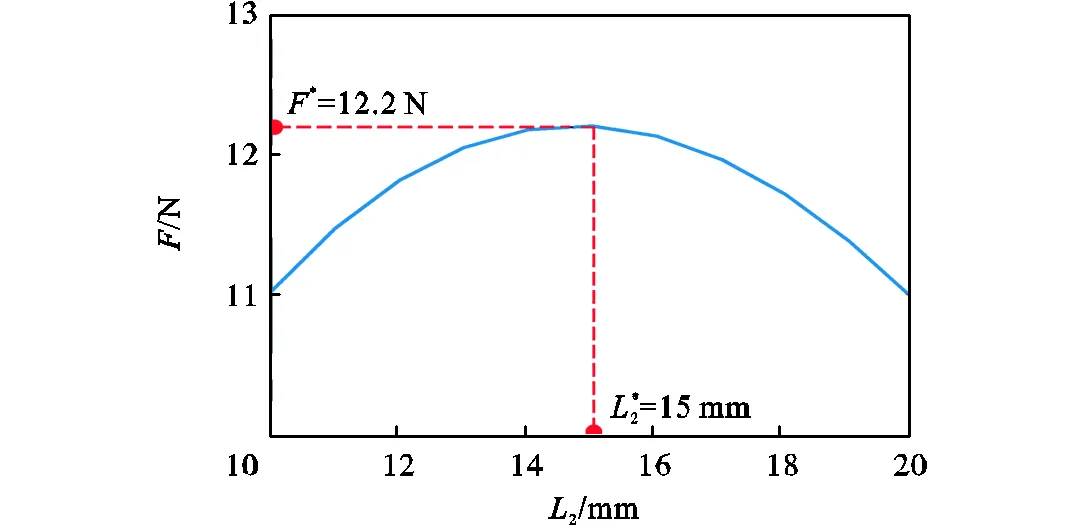
图7 L1、L 3、L4取最优值时F随L2的变化曲线

4 特性分析与模型验证

柔性驱动器在应用过程中可能受到冲击负载，导致变刚度装置内的永磁铁产生微小的位移从而偏离平衡位置，此时永磁铁应受到电磁引力的作用回到平衡位置，确保柔性驱动器正常工作．为验证柔性驱动器在工作状态下的稳定性，需要对该柔性驱动器的力-位移特性进行分析．将优化确定的最优参数值代入所建立的永磁铁受力模型中(式(12))，以平衡位置为原点，分别在正负方向上给定偏移量，利用MATLAB进行数值分析得到力-位移曲线(见图8)．由图可知，永磁铁所受电磁力与产生的位移线性相关，在偏离平衡位置任意一侧均受到电磁引力作用，永磁铁受到的回复力可使其回到平衡位置，保证了柔性驱动器在复杂作业环境中的稳定性．

为了研究柔性驱动器平衡外界动态负载的能力和响应情况，同时验证永磁铁受力模型的准确性，进一步分析两线圈分别通入线性变化的电流对电磁力大小的影响．将线性变化的电流(1＝2＋，2＝2－．其中＝0~2A)代入所建立的理论模型，并与仿真软件Ansoft的分析结果对比，如图9所示．由图可知，理论模型特性曲线与软件仿真曲线均反映出永磁铁所受电磁合力与通入电流的线性关系，且＝2A时两条曲线的误差达最大值，此时理论模型的计算结果为＝24.3N，软件仿真的计算结果为＝24.0N，二者误差为1.25%．上述结果表明，所建立的理论模型能够较为准确地反映该柔性驱动器的工作特性．

图8 力-位移特性曲线

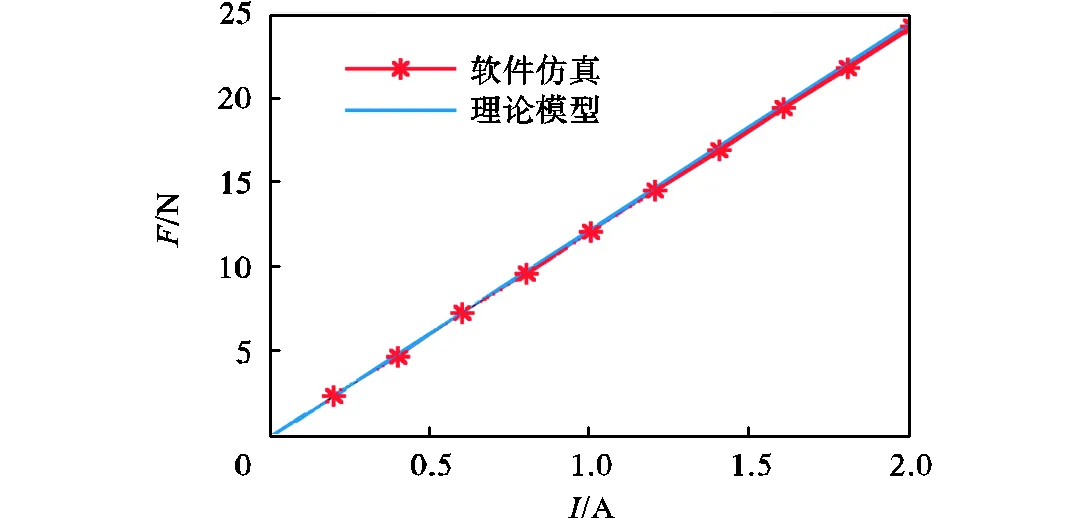
图9 力-电流特性曲线

5 实验验证

为了验证变刚度装置的实际工作特性和受力情况，按照优化得到的最优参数值搭建变刚度装置实验平台，如图10所示．为了将实验结果与理论结果进行对比，实验条件和方法全部与本文第4节相关内容保持一致，分别得到实验与理论对比的力-位移特性曲线和力-电流特性曲线(见图11和图12)．由图可知，实验曲线与理论曲线特性规律一致，图11中，两曲线在＝5mm时误差达到最大值，实验结果为＝-11.30N，理论结果为＝-12.42N，二者误差为9%．图12中，两曲线在＝2A时误差达到最大值，实验结果为＝22.72N，理论结果为＝23.78N，二者误差为4.5%．上述结果表明，本文所设计的变刚度柔性驱动器实验效果良好，方案具有可行性．

图10 变刚度装置实验平台

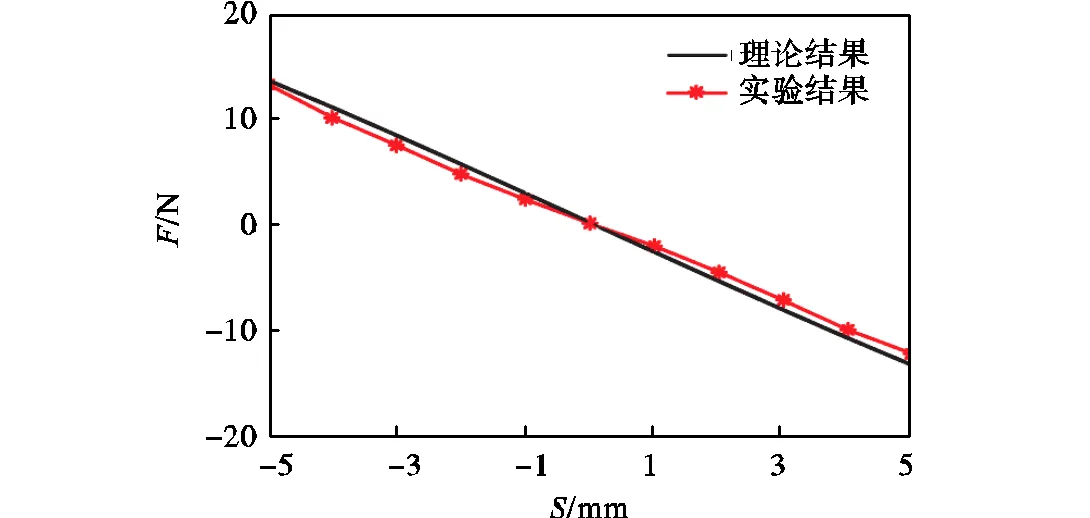
图11 力-位移特性实验验证

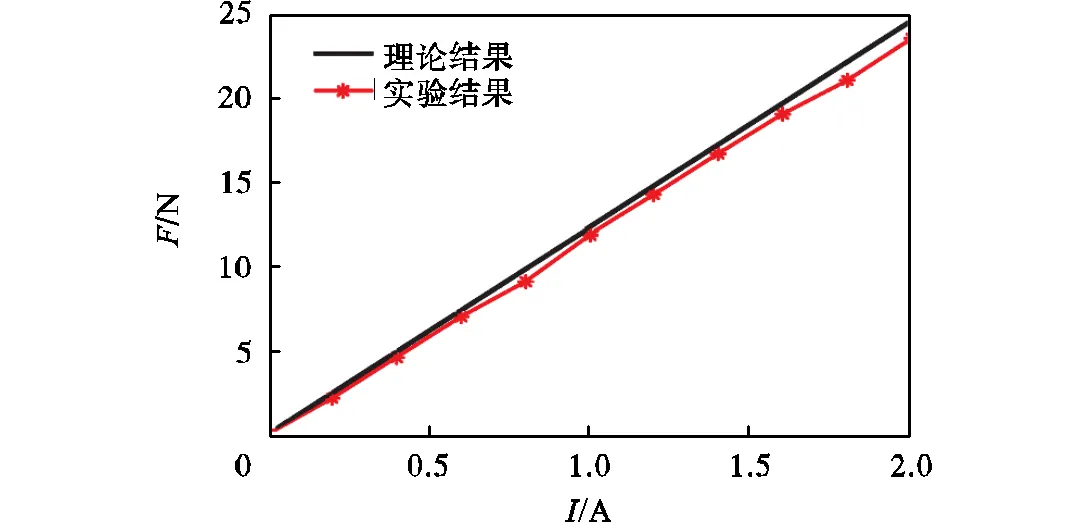
图12 力-电流特性实验验证

6 结 语

针对柔性驱动器自主创新性需求，以实现力位解耦控制为目标，设计了一种结构紧凑的电磁式柔性直线驱动器．依照其工作原理进行了电磁式柔性直线驱动器的概念设计，满足结构紧凑、响应速度快、可实现变刚度控制设计要求；基于电磁理论，建立了永磁铁的受力模型，并利用该模型得到永磁铁所受电磁力在各设计变量影响下的变化规律，确定了最优解；通过分析该柔性驱动器的力-位移、力-电流特性并进行实验验证，证明了所设计的柔性驱动器具有一定的抗负载扰动能力，揭示了其电磁力随电流线性变化的本质，验证了设计方案的可行性与有效性．本文的优化设计结果和力-位移与力-电流特性分析的实验结论对该柔性驱动器的实际应用具有重要指导意义．

［1］ Heinzmann J，Zelinsky A. Quantitative safety guarantees for physical human-robot interaction[J]. International Journal of Robotics Research，2003，22(7/8)：479-504.

［2］ Ham R V，Sugar T G，Vanderborght B，et al. Compliant actuator designs[J]. IEEE Robotics & Automation Magazine，2009，16(3)：81-94.

［3］ 魏敦文，葛文杰，高 涛. 仿生灵感下的弹性驱动器的研究综述[J]. 机器人，2017，39(4)：541-550.

Wei Dunwen，Ge Wenjie，Gao Tao. Review of elastic actuator research from bionic inspiration[J]. Robot，2017，39(4)：541-550(in Chinese).

［4］ Vanderborght B，Albu-Schaeffer A，Bicchi A，et al. Variable impedance actuators：A review[J]. Robotics & Autonomous Systems，2013，61(12)：1601-1614.

［5］ Wolf S，Hirzinger G. A new variable stiffness design：Matching requirements of the next robot generation[C]// IEEE International Conference on Robotics and Automation. Pasadena，CA，USA，2008：1741-1746.

［6］ Schiavi R，Grioli G，Sen S，et al. VSA-II：A novel prototype of variable stiffness actuator for safe and performing robots interacting with humans[C]// IEEE International Conference on Robotics and Automation. Pasadena，CA，USA，2008：2171-2176.

［7］ Jafari A，Tsagarakis N，Caldwell D. Energy efficient actua-tors with adjustable stiffness：A review on AwAS，AwAS-II and CompACT VSA changing stiffness based on lever mechanism[J]. Industrial Robot，2015，42(3)：242-251.

［8］ Kim B S，Song J B. Design and control of a variable stiffness actuator based on adjustable moment arm[J]. IEEE Transactions on Robotics，2012，28(5)：1145-1151.

［9］ Jafari A，Tsagarakis N G，Vanderborght B，et al. A novel actuator with adjustable stiffness(AwAS)[C]// IEEE/RSJ International Conference on Intelligent Robots and Systems. Taipei，China，2010：4201-4206.

［10］ Visser L C，Carloni R，Unal R，et al. Modeling and design of energy efficient variable stiffness actuators[C]// IEEE International Conference on Robotics and Automation. USA，2010：3273-3278.

［11］ Jafari A，Tsagarakis N G，Sardellitti I，et al. A new actuator with adjustable stiffness based on a variable ratio lever mechanism[J]. IEEE/ASME Transactions on Mechatronics，2013，19(1)：55-63.

［12］ Groothuis S S，Rusticelli G，Zucchelli A，et al. The variable stiffness actuator vsaUT-II：Mechanical design，modeling，and identification[J]. IEEE/ASME Transactions on Mechatronics，2014，19(2)：589-597.

［13］ Hollander K W，Sugar T G，Herring D E. Adjustable robotic tendon using a 'Jack Spring'™[C]// International Conference on Rehabilitation Robotics. Chicago，USA，2005：113-118.

［14］ Choi J，Hong S，Lee W，et al. A robot joint with variable stiffness using leaf springs[J]. IEEE Transactions on Robotics，2011，27(2)：229-238.

［15］ Tao Y，Wang T，Wang Y，et al. A new variable stiffness robot joint[J]. Industrial Robot，2015，42(4)：371-378.

［16］ 邬义杰，刘楚辉. 超磁致伸缩驱动器设计方法的研究[J]. 浙江大学学报：工学版，2004，38(6)：747-750.

Wu Yijie，Liu Chuhui. Study on design approach of giant magnetostrictive actuator[J]. Journal of Zhejiang University：Engineering Science，2004，38(6)：747-750(in Chinese).

［17］ 赵宏伟，孙立宁，张 涛，等. 压电陶瓷驱动器在机器人柔性臂应用中的研究[J]. 压电与声光，2000，22(3)：173-176.

Zhao Hongwei，Sun Lining，Zhang Tao，et al. The research of flexible manipulator driven by piezoelectric actuators[J]. Piezoelectrics & Acoustooptics，2000，22(3)：173-176(in Chinese).

［18］ 徐小兵，邓荆江. 形状记忆合金驱动器的研究现状及展望[J]. 机械研究与应用，2013(6)：187-190.

Xu Xiaobing，Deng Jingjiang. Recent progress and prospection of actuator based on shape memory alloys[J]. Mechanical Research & Application，2013(6)：187-190(in Chinese).

［19］ Delfino F，Manella A，Molfino P，et al. Numerical calculation of total force upon permanent magnets using equivalent source methods[J]. Compel International Journal of Computations & Mathematics in Electrical，2001，20(2)：431-447.

［20］ Pelloni S，Ligabue A，Lazzeretti P. Ring-current models from the differential Biot-Savart law[J]. Organic Letters，2004，6(24)：4451-4454.

(责任编辑：金顺爱)

Conceptual Design and Parametric Optimization of Electromagnetic Compliant Linear Actuator

Liu Haitao1，Wei Tianyuan1，Wang Youyu2，Liu Yuhua1

(1. Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education，Tianjin University， Tianjin 300350，China；2. Beijing Institute of Spacecraft System Engineering CAST，Beijing 100094，China)

In this paper，we describe our design of a compact electromagnetic compliant linear actuator，which can be used for force-position decoupled control．The actuator mainly comprises a variable stiffness device and a position adjustment device．We symmetrically placed two coils that interact with two permanent magnets in the variable stiffness device，in which the electromagnetic force can be adjusted to achieve variable stiffness by dynamically changing the input current in the coil．We then established a mathematical model of the magnetic field of the energized coil．Using this model，we derived the explicit expression of the electromagnetic force of the permanent magnet by the equivalent charge method．Furthermore，by analyzing the influence of the design parameters on the electromagnetic force of permanent magnet，we were able to optimize the variable stiffness device．Moreover，we analyzed the force-displacement and force-current characteristics of the variable stiffness device via simulation and experiment．Ultimately，we compared the experimental and theoretical results to verify the accuracy and effectiveness of the force-displacement and force-current characterizations of the device，The results confirm that the designed compliant linear actuator is suitable for variable stiffness control．

electromagnetic compliant actuator；conceptual design；optimization

10.11784/tdxbz201805025

TH13

A

0493-2137(2019)02-0166-07

2018-05-11；

2018-08-07.

刘海涛（1981—  ），男，博士，教授.

刘海涛，liuht@tju.edu.cn.

国家自然科学基金资助项目(51622508).

the National Natural Science Foundation of China(No. 51622508).