船载AIS和雷达数据关联及融合
2019-01-12俞金龙
俞金龙
(中船重工海声科技有限公司,宜昌,443000)
航运的发展使得海上交通安全导航成为一个重要的研究课题,而雷达和船载AIS是保障船舶航行安全的基本手段[1-9]。雷达可以得到水域全景的交通图像,除了所有运动的目标,还有静止的和固定的目标,以及其他环境信息等[6]。AIS的信息包含了船舶的船名、呼号、GPS位置、航向、航速、目的港等动态信息以及港口、天气、洋流等导航信息[4]。雷达数据更新快,但受环境影响较大,精度不高,目标分辨难度也较大。而AIS因通信方式不同,具有精度高和受限制因素小的优点,但数据更新慢。因此,在同时获得两者数据时,有必要将同一目标的信息进行融合,实现优势互补。雷达和AIS信息融合时基本上都采用分布式结构,如图1[3,5,6,8]。

图1 AIS与雷达信息融合结构模型
1 模型建立
1.1 数据预处理
1.1.1 坐标变换
统一两者坐标系,且坐标系以本船位置为坐标原点。
(1)AIS目标位置数据的坐标变换
AIS提供的目标位置数据实际上是由GPS接收器得到的。电子海图显示中一般需要将大地坐标的经纬度通过墨卡托投影转换成平面坐标,墨卡托投影变换公式如下:

式中
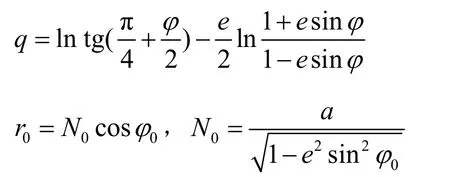
式中,q称为等量纬度,r0称为基准纬度圈半径,N0称为基准纬度处椭球的圈曲率半径,φ0为墨卡托投影变换的基准纬度,(φ,λ)为WGS-84坐标系的经纬度,(x,y)为墨卡托平面直角坐标,a为地球长半径,e为椭球的第一偏心率。
(2)雷达目标位置数据的坐标变换
雷达探测接收到的数据可在极坐标下进行显示,测量得到的数据包括距离R和旋转角度θ,(XR,YR)表示雷达目标位置数据的直角坐标。

1.1.2 时间对准
雷达的扫描周期一般为15~30 r/min,扫描周期2~4 s,比较固定。自动模式下,船舶不同状态时AIS广播的动态信息间隔是不同的,见表1[6],因此需要将雷达和AIS的目标信息进行时间对准[2-5,7-9]。

表1 AIS动态信息报告间隔
假定在同一时间段内AIS和雷达的采样时刻分别如下:
(1) AIS的采样时刻序列F个:

(2)雷达采样时刻N个序列T个:

1.1.3 时间插值
由于雷达扫描周期固定,并且时间较短,而运动目标短时间内可近似为匀速直线运动,所以本文采取线性插值的方法。设T1<T<T2,AIS在T1、T2采集的位置信息分别为(λ1,φ1)、(λ2,φ2),则在T时刻AIS目标的位置信息为[2]:

1.2 航迹关联
利用柯西型隶属度函数做模糊关联时,要比正态型的关联正确率高很多[9]。本文采用柯西隶属度加权方法进行航迹关联。柯西型分布是连续的概率分布,柯西函数曲线如图2所示,其概率密度函数如下:

式中,x0是定义分布峰值位置的位置参数,γ是最大值一半处的一半宽度的尺度参数。取x0=5,γ=6,并除以最大值归一化处理得到图2。

图2 柯西函数曲线
柯西型隶属度函数:

式中,ξ(ηk)为模糊因素中第k个因素的柯西型隶属度函数,ηk和λk分别为模糊因素中第k个因素的欧氏距离和展度。欧式距离计算方法:

式中,k=1,2,3,4(分别表示距离、方位、速度、航向)ηk(i)为各因素的欧氏距离,LRK(i)和LAK(i)分别为通过雷达和AIS获得的i时刻的第k个因素值。
模糊因素的展度与航迹的误差分布有关,故取各因素欧式距离的均方根值作为每个模糊因素的展度[9]:

得到各单因素的隶属度函数值,利用加权的方法计算综合相似度:

式中,用γ的最大值确定航迹的相关性。
1.3 航迹融合
由最小均方误差可以确定如下权融合算法[9],权重由二者的测量精度获得,即[8]

这里,WRL+WAL=1,δRL、δAL为雷达和AIS关于因素L的精度,WRL、WAL分别为对应加权因子。融合后的数据为:

2 仿真分析
2.1 仿真理想航迹
选取4个运动目标,假定本船为静止,并且位置为(0,0)。测量因素集选取:

目标的轨迹真值如图3(a)所示,距离真值信息如图4(a)所示。
2.2 仿真测量航迹
仿真选定60 s内目标运动信息,设雷达扫描周期为3 s,AIS的目标更新率分别为A船5 s、B船2 s、C船4 s、D船6 s。设雷达和AIS的距离、方位、航速、航向精度分别为

测量对准后的目标运动轨迹如图3(b)所示,测量距离信息如图4(b)所示。
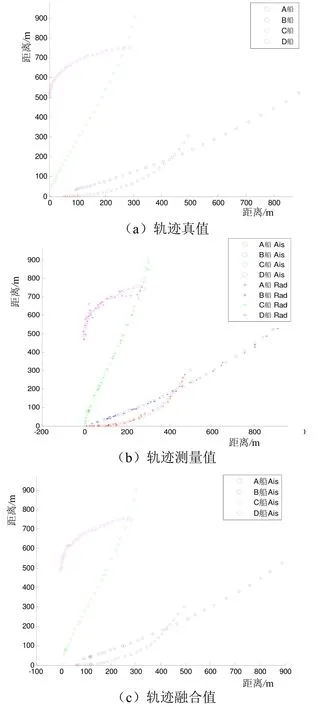
图3 目标轨迹真值、测量值和融合值对比图
图中,值得注意的是A船和B船的航迹较为接近,B船和C船相距坐标原点的距离较为接近,B船和C船速度较为接近,以此来增加关联判别难度。
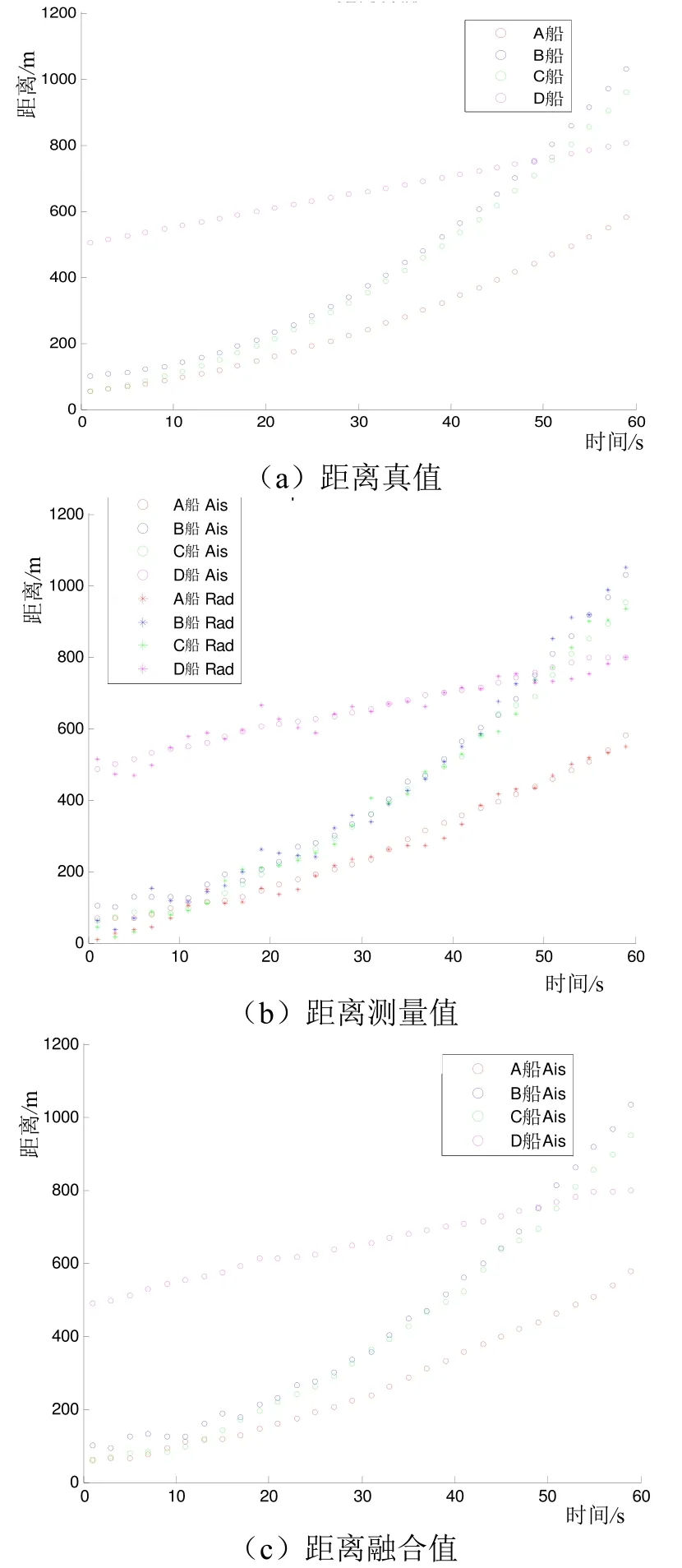
图4 目标距离真值、测量值和融合值对比图
2.3 航迹关联结果
根据1.2中提出的方法进行航迹关联。考虑到数据动态更新中相关重要度,动态信息主导作用依次为距离、方位、航速、航向。我们令因素集

文献[9]通过对多组不同模糊因素权值分别进行仿真分析,因素集中对应的权值选取依次为
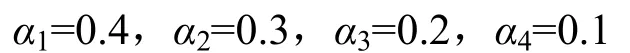
由式(9)得到航迹的相关性γ表,如表2所示。

表2 柯西隶属度-模糊因素集关联值
由表中γ值可以看出,γ最大值确定航迹的相关性,与1.2中结论一致。
2.4 航迹融合结果
通过2.2中雷达和AIS相关精度信息,再由式(10)~(12),对于距离、方位、速度、航向这些因素值,计算可得对应加权系数值:
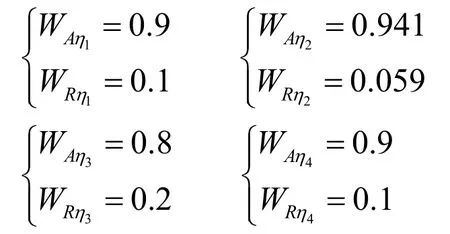
融合后航迹如图3(c)、图4(c)所示。可以看出,融合后的航迹、距离接近于真实航迹。
2.5 误差分析
数据融合后的距离误差,如图5所示。从图中可以看出,融合后的距离误差略优于雷达和AIS结果,并且更接近于AIS距离误差,主要是因为AIS的精度高于雷达测量精度,但其缺点是数据更新相较于雷达慢。

图5 时刻对准融合后距离误差对比图
3 结论
雷达与AIS信息融合是典型多因素信息优势互补的应用实例。本文首先给出了一种便于工程实现数学模型。然后,对模型中航迹信息关联和融合部分进行了仿真验证。其结果成功对航迹进行了关联,并且得到了优于雷达和AIS的单独获得的结果。
