基于CFD的螺旋桨水动力性能研究

陆军 陈万 张玉

（哈尔滨工程大学，哈尔滨，150001）

螺旋桨因其水动力性能优越、工作效率高，是现代舰船首选的推进器[1]。不同类型的船舶，往往选取不同种类的螺旋桨，常用的有对转螺旋桨、串列螺旋桨、可调螺距螺旋桨以及导管螺旋桨等。近年来我国的船舶技术发展迅速，高速舰船不断涌现，其中，由邹劲等人设计的HST1300滑行艇，是一种具有断级结构的三体滑行艇，该滑行艇独特的M型槽道使其具有优良的性能，同时该滑行艇在推进器的选择上，采用了特殊的双桨双舵，桨舵一体结构，该结构相对于普通螺旋桨，不仅能够在滑行艇前进过程中提供足够的动力，同时，还可以通过改变螺旋桨的角度达到改变舵角的目的[2-4]。

螺旋桨最早出现于1809年，经过200多年的发展，已经形成较为成熟的理论体系[5]。在螺旋桨的性能研究过程中，最常用的方法主要有：敞水试验法，即利用模型进行运动模拟；理论计算，根据桨叶形状等进行理论分析计算；数值模拟，即利用计算机进行螺旋桨的水动力分析[6]。CFD（Computational Fluid Dynamics）方法是随着计算机技术的发展逐渐成熟的一种分析方法，在利用CFD软件，如FLUENT、AQWA等进行螺旋桨性能分析时，可以实现结果的可视化，螺旋桨的压力分布、力和力矩等都可以进行全面的展示，同时可以克服在敞水试验方法中出现的时间长、费用高等缺点，也充分考虑了流体粘性的影响，是一种较为理想的试验方法[7-10]。系统辨识是根据系统的输入输出观测数据来寻找一个函数或者系统来逼近实际系统。本文通过对HST1300三体滑行艇使用的E779A螺旋桨采用CFD进行数值模拟获得敞水条件下的推力系数和转矩系数，与试验值基本吻合，结合经验公式获得的伴流系数和推力减额对计算结果进行修正，得到该螺旋桨运动的数学模型。

1 E779A型螺旋桨

HST1300三体滑行艇采用双桨双舵、桨舵一体结构，两个螺旋桨采用完全相同的E779A型标准桨，双桨分别与双舵相连，同时双桨又通过一根横向机械杆相连，如图1所示。这种特殊的结构可以使螺旋桨在对三体滑行艇产生推力的同时，还可以通过 360°的摇动来对滑行艇的航向、航速以及运动姿态进行控制。由于两个螺旋桨完全相同且结构对称，为了方便我们只对其中一个进行分析研究[11]。

图1 螺旋桨和舵模型

1.1 螺旋桨的几何参数

E779A螺旋桨是1959年设计的四叶、定螺距、低侧斜螺旋桨，该螺旋桨的详细几何参数如表1所示。我们根据螺旋参数化建模方法可以绘制出E779A螺旋桨的几何模型，其3D模型如图2所示。

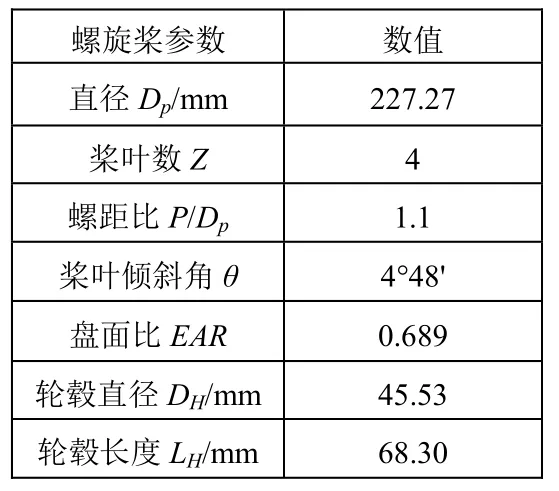
表1 E779A螺旋桨几何特征参数

图2 E779A螺旋桨3D模型

1.2 螺旋桨的推力和转矩

螺旋桨的推力主要跟螺旋桨的直径Dp、主机控制的螺旋桨转速n、进速VA、水密度ρ、水粘性系数v和重力加速度g有关，即：

式中，VA/nDp为进速系数J，为雷诺数Re，相当于傅汝德数Fn，Fn与水面的兴波情况有关。

由于HST1300在正常航行时速度高于70 kn，所以在前进过程中会产生较大的波浪，但是滑行艇独特的M型槽道可以有效的吸收船兴波。同时，在上述公式中，当桨的浸沉深度达到一定要求，即hs＞0.625Dp时，船兴波对螺旋桨推力的影响可以忽略不计；另外，当雷诺数超过流体的临界雷诺数，则雷诺数不再引起流体流动性能的改变。由于在该三体滑行艇前进过程中，Re＞＞Rec，所以，对于一定形状的螺旋桨，上述公式可以简化为：

式中，KT为推力系数。

同理，对于螺旋桨转矩有：

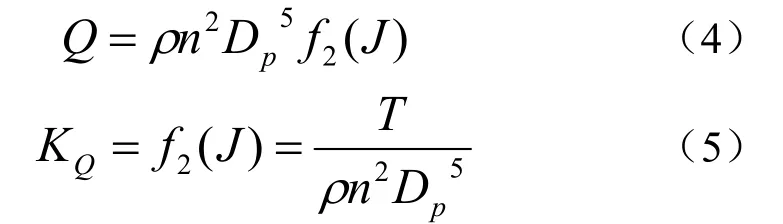
式中，KQ为转矩系数。

2 螺旋桨数值模拟

2.1 湍流模型选取

通过CFD方法求解RANS（Reynolds Average Navier-Stokes）方程，是螺旋桨水动力研究的一种新途径。在研究中影响计算精度的原因主要有两个：一是对螺旋桨网格的划分；二是湍流模型的选取。模型的选取必须充分考虑流场在船舶运动过程中的特点，以及所需的精度等条件[12-13]。为了模拟E779A螺旋桨在工作过程中的状态，根据相对性原理，我们假定螺旋桨处于轴向静止状态，水流以一定的速度流动并且围绕螺旋桨周向进行转动，且速度较大。通常情况下，假定流体是不可压缩的，则流场的控制方程选取不可压缩流体RANS方程，其中，质量方程：

动量方程为：

湍流耗散率ε方程为：

式中，Gk为由于平均速度梯度引起的湍动能产生项；Gb用于浮力影响引起的湍动能产生项；YM为可压速湍流脉动膨胀对总的耗散率的影响。

2.2 计算域与网格划分

对螺旋桨进行网格划分，是CFD模拟过程中要求最高、耗时最长的环节。网格的数量和质量决定着计算的效率。无论网格稠密还是稀疏都对计算结果不利。网格稠密，则意味着计算量较大甚至会使计算不收敛，而网格过于稀疏会大大降低准确度[15]。为了使网格划分和数值计算更加简洁高效，对于E779A螺旋桨，网格划分如图3所示。该网格使用ICEM软件生成，根据流场特点，将计算域划分为内外两个，采用不同的坐标系进行计算，外流场采用固定坐标，一般取长度为10D（D为螺旋桨直径），直径为5D的圆柱形模拟流场；内流场采用旋转坐标，一般取直径为1.2D，用以模拟螺旋桨的转动。静止区域采用结构化网格，旋转区域使用非结构化网格，同时使用局部加密的方法，对叶梢、叶根等部分进行局部加密[16-17]。

图3 E779A螺旋桨壁面网格

2.3 边界条件设定

边界条件设定如下：进口边界采用速度入口，给定入口速度（即来流速度），同时给出各速度的分量，入口速度由下式得到：

采用压力出口边界，出口压力由下式给定：

经过计算得到湍流动能k=0.153 m2/s2，比耗散率ω=100 s-1，旋转速度n=900 r/min。对于螺旋桨表面，由于受到流体粘性的影响，所以设置该螺旋桨表面为不可滑移表面。对于流场控制方程，对流项采用二阶迎风差分格式，扩散项采用中心差分格式，压力耦合方程使用SIMPLE算法[18-20]。

2.4 数值分析结果

为了获取螺旋桨的特性曲线，给定螺旋桨的工作转速为900 r/min，保持转速不变，进速系数的范围取 0.5～1.0，通过改变来流的速度来实现进速系数的变化。通过模拟计算，可以得到螺旋桨表面的宏观受力，即螺旋桨的推力和转矩，结果见表2。

表2 不同进速系数下推力和转矩

3 数值计算结果分析

3.1 特性曲线拟合

通过式（3）和（5）可以分别求出对应的推力系数KT和转矩系数KQ，与查询资料所得的实验值相比较，得到该螺旋桨的特性曲线，如图4所示。通过曲线可以看出，CFD数值计算得到的螺旋桨特性曲线与实验值基本吻合，进速系数在0.8附近效率最高。但是这种表达方式没有明确的函数表达式，不利于螺旋桨的运动建模和仿真计算，为此需要建立一个简洁且精度符合要求的近似表达式，一般可表示为下列形式：

图4 E779A螺旋桨特性曲线

按照上述形式对螺旋桨的推力系数和转矩系数进行曲线拟合，考虑到计算量和精度问题，采用三阶拟合来实现。可以得到推力系数与进速系数、转矩系数与进速系数之间的拟合关系。拟合结果如表3所示。

表3 螺旋桨特性拟合结果

3.2 滑行艇与螺旋桨的相互作用

3.2.1 滑行艇多螺旋桨的影响

螺旋桨是在滑行艇尾部进行工作的，所以会受到滑行艇尾流的影响。航行过程中，对螺旋桨产生影响的尾流主要有三种：由于流体的粘性作用而产生的摩擦伴流；尾部与其他部分的压力差造成的位差伴流；航行过程中的波浪而产生的波浪伴流。这些伴流使水流过螺旋桨的速度与滑行艇的前进速度不同，螺旋桨相对于水的速度可以表示为：

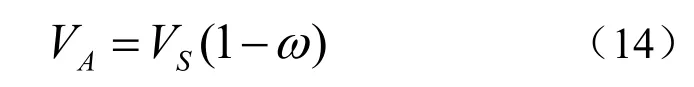
式中，VS为滑行艇的前进速度，ω称为伴流系数。伴流系数与螺旋桨的位置、尺寸以及船型有关，通常采用经验公式进行计算，对于双桨船，有霍尔特洛公式：

式中，B为船宽，dm为吃水，Cb为方形系数，Cv为粘性阻力系数。将HST1300滑行艇和E779A螺旋桨的各项数值代入式（15）可得伴流系数为0.2。

3.2.2 螺旋桨对滑行艇的影响

螺旋桨在滑行艇尾部工作时，整个工作区域属于低压区，尾部压力的减小使滑行艇的阻力增大，同时尾部水流速度的增加也会使滑行艇阻力增加，由于螺旋桨的作用增加的这一部分阻力成为滑行艇的阻力增额。螺旋桨在工作时产生的推力T，一部分用于克服滑行艇自身的阻力R，另一部分用于克服阻力增额ΔR,即：

所以有效推力表示为：

通常将ΔR称为推力减额，则推力减额系数表示为：

推力减额系数与螺旋桨的位置、尺寸以及船型有关，通常采用经验公式来确定。对于双桨船，有霍尔特洛公式：

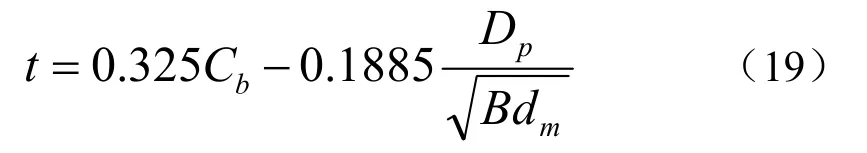
经过计算可得推力减额系数为0.1。

3.3 基于滑行艇的螺旋桨运动模型

滑行艇的运动过程可表示为：

式中，m为滑行艇的质量，Δm为滑行艇在运动过程中的附着水质量。附着水质量一般取滑行艇质量的 5%～15%，为了便于计算，本文中取 10%，滑行艇在运动过程中受到空气和水两种介质的阻力，但是以水阻力为主，空气阻力较小。船舶的两类阻力均随着船速的增大而增大，在一定条件下总阻力可简化为：

式中，r为阻力系数，对于确定的航行工况，系数r为常数。滑行艇在高速滑行过程中r的取值通常1.5。综合上述分析，可以得到螺旋桨的运动模型如图5所示。

图5 E779A螺旋桨运动模型

螺旋桨运动模型中，转速由外部输入，在给定初始运动状态时，滑行艇的速度通过求解运动方程获得。输出量是螺旋桨的推力和转矩。

4 结论

基于CFD的辨识建模是目前较为理想的螺旋桨水动力性能分析方法，通过对螺旋桨的3D模型进行数值模拟以及对数据进行拟合，获得螺旋桨的特性曲线，并与实验值进行比较，得到三阶拟合关系式。螺旋桨和船体之间相互作用力复杂，通过近似分析，将滑行艇和螺旋桨作为一个整体，得到螺旋桨运动的数学模型。以往的研究中，大都对船-桨-舵整体建模研究，本文主要对螺旋桨进行运动建模。E779A螺旋桨是滑行艇主流螺旋桨，得到其运动模型对于滑行艇螺旋桨的设计和分析螺旋桨与船体之间的相互作用具有重要意义。该模型作为滑行艇运控模型的一部分，用于船舶运动控制器的设计。文中只假设了螺旋桨处于轴向静止状态，水流速度较快且定速。为了得到螺旋桨更加精确的性能需对螺旋桨的非定常状态下，多相流的流动进行分析，而这需要更复杂的模型，此外，随着研究的深入，广大科研人员均发现 RANS方程在高速状态下的数值计算并不十分准确，仿真值与实验值相比仍有一定误差，其中的原因需要进一步对理论进行研究。