多元IV型弯张换能器半波长布阵仿真研究
2019-01-12陈立纲马振
陈立纲 马振
(1.海军驻杭州地区军事代表室,杭州,310023;2.第七一五研究所,杭州,310023)
IV型弯张换能器由驱动振子、振动壳体等部件组成。换能器工作时振子的伸张、收缩驱动壳体的弯曲振动并进行声辐射。IV型弯张换能器具有低频、大功率、小尺寸的特点(典型的IV型弯张换能器最大线性尺寸约为谐振波长的1/4),主要工作于0.3~3 kHz频率范围。为了满足声源级和指向性的要求,换能器常需要组成阵列工作。成阵的方式有半波长布阵和密排布阵等。其中半波长布阵是指相邻两个换能器声中心间距等于谐振处波长的一半。半波长布阵的主瓣声源级高,无栅瓣。对于IV型弯张这类低频换能器而言,半波长布阵情况时,有限元模型需要更大的声场。本文分析了声场尺寸对换能器性能的影响,并推导了声场应满足的尺寸要求。
1 单个IV型弯张换能器仿真
换能器成阵前首先应确定单个换能器性能。单个IV型弯张换能器壳体长轴为250 mm、短轴为130 mm、高为100 mm、厚度为15 mm。结构如图1所示。利用Comsol有限元软件建模如图2,其中有限元水域半径为2 m,外侧设置球面波扩展模拟无限大水域,进行水中谐响应仿真并提取相关结果见图3~图5。

图1 弯张换能器模型

图2 水中有限元模型

图3 长轴方向发送电压响应
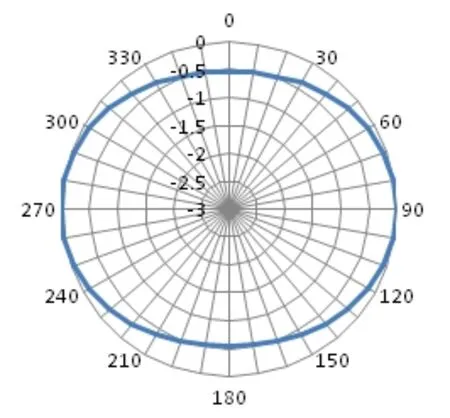
图4 长轴-高度平面指向性
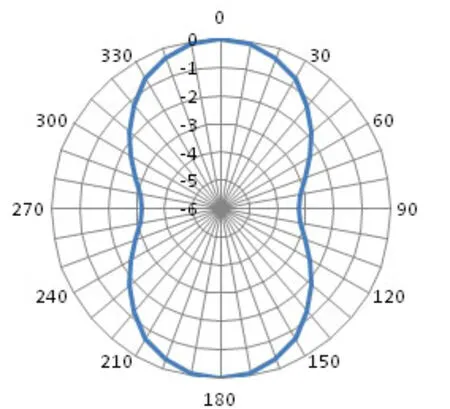
图5 长轴-短轴平面指向性
仿真显示单个换能器谐振频率约为1.8 kHz,长轴发送电压响应约为141.5 dB。从指向性图上可以看出,长轴-高度平面换能器响应最大起伏为0.5 dB(其中0°为高度方向,90°为长轴方向);长轴-短轴方向最大响应起伏为3 dB(其中0°为长轴方向,90°为短轴方向)。可以看出,换能器响应在空间上起伏较小,尤其是长轴-高度平面可近似看做无指向性。
2 两种方法计算半波长布阵性能
针对 IV型弯张换能器短轴方向响应较小的特点,将换能器沿短轴方向半波长布阵。分别布2元、4元、6元、8元、10元阵,并用经典理论和有限元计算响应与指向性性能。
2.1 经典理论计算
沿短轴方向布阵,单个换能器布阵方向上最大尺寸(短轴长度)约为波长的1/6,换能器尺寸远小于谐振时波长,换能器空间上响应起伏较小,因此可以用经典半波长布阵计算公式估算阵列的响应与指向性。公式如下[1]。

式(1)为半波长线阵的指向性计算公式,式(2)是半波长布阵情况下阵列发送电压响应计算公式。其中N为阵元个数,d为布阵间距(这里取波长的一半),λ是谐振时波长(这里取1.8 kHz为谐振频率),svl是单个换能器发送电压响应,SVL是阵列的发送电压响应,D(π/2,θ)是阵列高度方向(换能器短轴-高度所在平面)上指向性,其中θ=0为过阵列声中心垂直于线阵的方向。计算响应随阵元个数变化的结果见表1。计算高度方向指向性结果见图6和表2。从表1可以看出随着阵元个数的增加,阵列的发送电压响应逐渐增高;从图6和表2可以看出,半波长布阵情况下阵列无栅瓣,旁瓣级逐渐降低,–3 dB波束宽度逐渐减小。

表1 不同阵元数下的响应
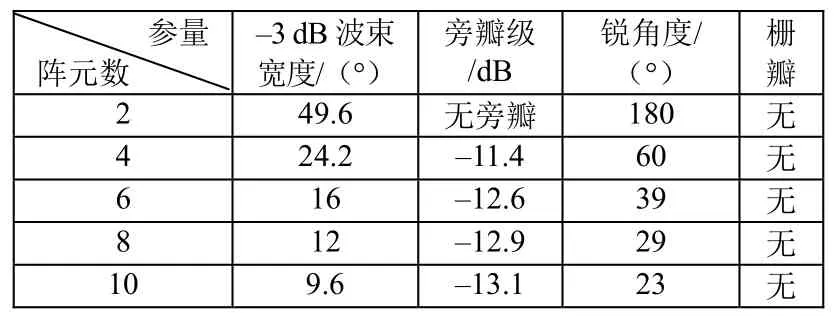
表2 不同阵元的指向性参数

图6 高度方向指向性
2.2 有限元建模分析
沿短轴方向布阵,分别建立2元、4元、6元、8元、10元阵列模型。布阵间距为1/2波长(1.8 kHz频率处),有限元水域半径为3 m,水域外侧设置球面波扩展模拟无限大水域。其中十元阵的 1/8模型如图7。分别计算2元、4元、6元、8元、10元阵列的发送电压响应和指向性结果见表3、表4和图8。

图7 十元阵有限元模型

表3 不同阵元的发送电压响应
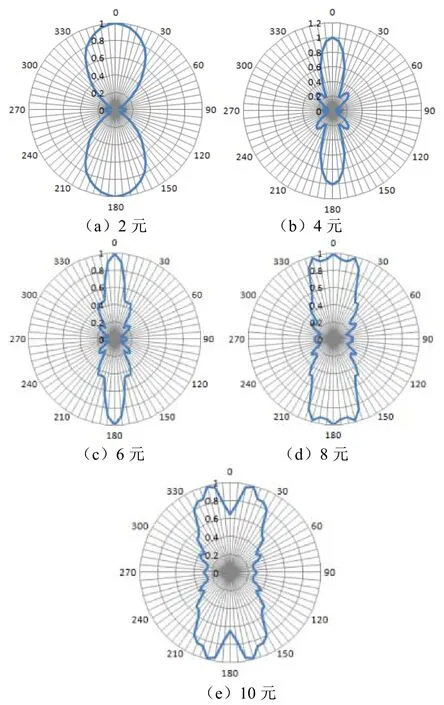
图8 高度方向指向性

表4 不同阵元的指向性参数
从仿真数据可以看出,随着阵元个数的增加阵列发送电压响应先增大(2元~6元)后减小(6元~10元);从指向性图可以看出,从6元~8元,阵列主瓣逐渐变得平坦,10元阵列的主瓣位置出现凹谷,凹谷两边出现四个栅瓣。
2.3 对比分析
对比两种方法计算的响应如图9。从图中可以看出,理论计算的响应结果随阵元数的增加而增大,有限元计算的响应随阵元数的增加而先增大(2元~6元)后减小(6元~10元)。理论计算的响应值要大于有限元计算的响应值,并且二者差值随阵元数的增加而逐渐增加。另外应当注意的是在 2元、4元时,理论计算值与有限元计算值比较相近。

图9 两种方式计算响应对比
通过对比可以看出两种计算方法在计算2元、4元、6元的指向性的结果相近,8元、10元的计算结果相差很大。其中从6元~8元的–3 dB波束宽度反而增大以及10元阵0°、180°方向出现凹谷这两种现象与实际工程经验相违背。
综上可以得出,在本例的模型条件下,随着阵元数的增加,有限元仿真结果与经典理论计算结果的差别越来越大。
3 现象解释与声场尺寸计算
3.1 现象解释
利用经典理论公式计算阵列的性能时需满足“点源”和“基元间隔”两个条件[1]。本例中的IV型弯张换能器基本满足上述条件,所以用经典理论计算的结果应与实际测试结果相接近。但有限元计算结果与经典理论相差较大,并且这种差别随阵元个数的增加而变大,这种现象的主要原因是有限元模型中水域尺寸较小,不能满足计算发送电压响应和指向性的声场条件。解释如图10。

图10 两种方式计算响应对比
图10中o点为声中心,a为观测点,b为阵列中任意阵元声中心,其中观测点距声中心的距离为x,阵元声中心距阵列声中心距离为y,阵元声中心距观测点距离为r,r=sqrt(x2+y2)。可以计算出各阵元到观测点(x=3 m)与声中心到观测点的声程差见表5。

表5 不同声中心下的声程差计算表
为了解释声程差对观测点响应的影响,这里记观测点处接收到的不同阵元的声压之和为:
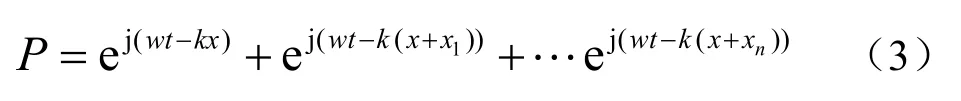
式中P为总声压,w为角频率,k为波数,xn为声程差。ej(wt-kx)为接收中心点的声压(实际阵列中可能不存在,此处为了解释简单而引入);ej(wt-k(x+xn))为接收到与中心点声程差为xn的阵元的声压。为了简化计算,上式中忽略阵元与接收点距离对声压的幅值影响,可改写为:

为了简化计算,这里仅取X1进行分析。

上式中k=2π/λ,其中λ是谐振波长。可以看出,当x1<λ/4 时二者正相叠加;当λ/4<x1<3λ/4 时二者反相叠加;当λ3/4<x1<λ时二者正相叠加。对于本例中的阵列,从2元阵到10元阵,阵元声程差逐渐增大,其中2元~6元阵列的声程差小于λ/4,8元、10元的声程差大于λ/4小于3λ/4。所以从2元~6元,观测点的响应逐渐增大,但由于声程差逐渐变大,有限元计算的响应值与经典理论的计算值差别随阵元数的增加而增大;从8元~10元,声场反相叠加,观测点的响应逐渐减小,并且在指向性图上逐渐出现凹谷。
3.2 声场尺寸计算
用有限元软件计算阵列响应与指向性时声场尺寸也应满足远场条件,即任意两阵元到中心观测点的声压的幅值与相位均相同(声线平行)[2]。这一条件可转换为距声中心最远的阵元到观测点与声中心至观测点的声程差小于1/4波长:

当声程差取为1/4波长的1/10时,可计算自由场水域尺寸为:

对于半波长布阵,谐振频率为1.8 kHz的换能器的线阵,可求出不同阵元数下自由场水域尺寸,见表6。

表6 不同阵元数下声场尺寸
针对上述结果分别对2元与4元阵进行仿真分析,图11、图12为响应随水域半径增大的变化。

图11 2元阵响应随水域半径变化

图12 4元阵响应随水域半径变化
从图中可以看出,对于2元阵,随着水域尺寸从1 m变大到6 m,响应从146.5 dB增加到147.2 dB,并逐渐趋近于理论计算值147.5 dB;对于4元阵,随着水域尺寸从1 m变大到6 m,响应从149.2 dB增大到153 dB,也逐渐趋近于理论计算值153.5 dB。2元阵在水域尺寸为1 m的情况下响应值与理论计算仍有约1 dB的差别,这主要是因为换能器尺寸相对于声场尺寸过大,不能看做点源。综上可以看出,用有限元对阵列进行仿真时,声场尺寸对阵列的响应与指向性均有较大影响,为了获得较为准确的计算结果,声场尺寸应满足一定的尺寸条件。
4 总结
本文通过对比经典理论和有限元仿真,分析了有限元水域尺寸对仿真数据的影响,解释了水域尺寸影响仿真结果的机理,并在此基础上推导出阵列仿真时水域应满足的尺寸要求。需要说明的是本文中选取的远场条件为四分之一波长的 1/10,在实际建模中应根据计算量和计算精度选取合适的远场条件。另外在阵元数较多,模型较大的情况下,可以使用有限元与边界元相结合的方式减小计算量。
