海底衰减系数对舰船地震波的影响

张建民 安俊英

(中国科学院声学研究所北海研究站，青岛，266112)

舰船地震波是舰船航行过程中产生的低频辐射噪声激发弹性海底产生的，通常意义下的舰船地震波指的是Scholte波。实际工程应用中，海底表面传感器测量到的不仅包含Scholte波，也包含其他弹性波，比如简正波、广义 Rayleigh波等，因此本文中的舰船地震波指的是海底表面可以测量到的所有弹性波。

目前对舰船地震波的理论研究主要分为地震波形成机理分析、舰船地震波场的仿真计算以及实验测量等。文献[1]指出，在浅海传播条件下，海底声学特性对低频和极低频声波传播的影响几乎是决定性的，论证了舰船地震波在水中目标探测中的重要应用前景。文献[2]通过波数积分方法详细研究了海底参数、声源频率及深度、海水深度及声速剖面等因素对海水以及海底中声场空间分布的影响；同时采用抛物方程方法研究了斜坡海底情况下舰船地震波的传播规律，并进行了岸上舰船地震波的实验测量。文献[3-4]研究了海洋参数对Scholte波传播特征的影响以及水平分层情况下Scholte波的频散特性、质点运动轨迹和位移分布。文献[5-7]研究了浅海低频多层介质中的声传播理论，并进行了传播损失的计算；还建立了浅海地震波传播的简正波模型，分析了在浅海海底传播的地震波传播效应；利用安装了地震波传感器和水听器的圆柱型水密舱测量得到地震波和辐射噪声信号，并进行了频谱分析。文献[8-9]研究了舰船辐射噪声引起地震波的波动方程和有限元数值计算模型，并对二维半无限空间层状海洋环境下的地震波信号进行了数值模拟，并分析了其形成机理。

本文通过求解波数积分方法中积分核函数的极点值，分析了不同海底类型以及有无衰减情况下，Scholte波与简正波的相速度的变化以及对海底表面声场的影响。

1 理论模型

1.1 波数积分方法

对与距离无关的水平分层介质模型，可采用积分变换的数值实现方法，声场解的形式是深度分离波动方程的谱积分（波数积分）。要确定距离为r、深度为z位置处的声场g(r,z)，必须对深度分离的波动方程解的逆Hankel变换进行计算。

式中，kr为水平波数，g(kr,z)为积分核函数，Jm(x)为m阶Bessel函数。

用快速声场近似求解时，积分式中 Bessel函数用 Hankel函数表示，忽略与入射波有关的项，并将表示为渐近形式，从而得到逆Hankel变换的表达式为

对于不同的波导，积分核函数g(kr,z)的极点是变化的。不同的极点值对应不同类型的波，比如Scholte波、波导简正波、衰减简正波等。

1.2 极点求解

柱坐标系(r,φ,z)中，声源沿垂直轴z轴分布，则声场与方位角φ无关。海水中声场势函数分别表示为

海底中声场势函数分别表示为

式中，k1z和k2z、κ2z分别为海水与海底中z方向的波数；A+、A-、B、C为待定系数。

海水流体介质中，垂直位移w(r,z)与声压p(r,z)分别表示为

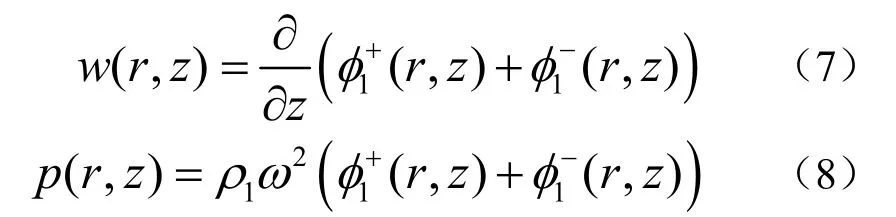
海底弹性体介质中，垂直位移w(r,z)与水平位移u(r,z)分别表示为

法向应力σzz(r,z)和切向应力σrz(r,z)的表达式为

假设点声源为位于水深zs处，点声源强度为Sw，根据海水表面与海底表面处的连续性边界条件，可得

式中，ρ1、ρ2分别为海水、海底密度，H为海水深度。求得势函数表达式中的待定系数后，即可采用波数积分方法对声场进行仿真计算。积分核函数的极点等同于式（13）中系数矩阵的求解存在非平凡解，即系数行列式等于零。

2 数值仿真

仿真计算时，假设海水深度75 m，密度为1 000 kg/m3，声速为1 500 m/s。弹性海底声学参数从表1中选取，海底从软变硬，近似于沙子、砾石、岩石三种类型。

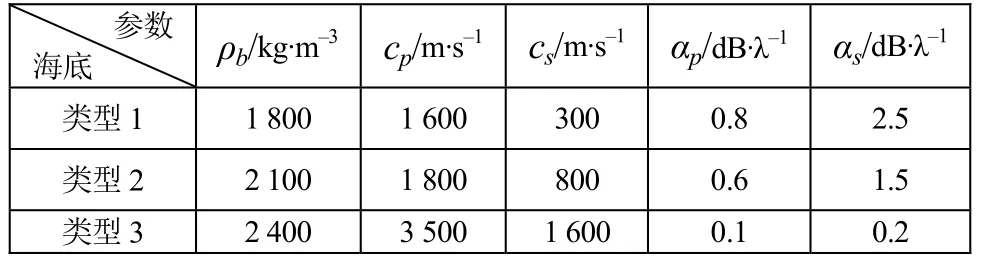
表1 不同弹性海底声学参数

表1中ρb表示海底密度，cp、cs分别表示海底压缩波速度、剪切波速度，αp、αs分别表示海底压缩波衰减、剪切波衰减。

为了便于分析声波对不同类型海底表面声场的影响，假设幅度为1的点声源靠近海底，声源深度70 m。为了能更清晰的分析海底声学参数对舰船地震波的影响，对海底表面声场的绝对值取以10为底的对数后再画图表示。

由于衰减简正波只近距离传播，以下仿真计算时只求解Scholte波、波导简正波以及1个衰减简正波的极点。声源频率25 Hz时，不考虑衰减的情况下，各类极点值与相速度分别如表2、表3所示。由极点值可知，Scholte波的相速度小于对应的海底剪切速度，简正波相速度大于海水中声速。1类和3类海底类型时存在波导简正波和衰减简正波；2类海底只存在衰减简正波。

表2 不考虑海底衰减，各类极点值

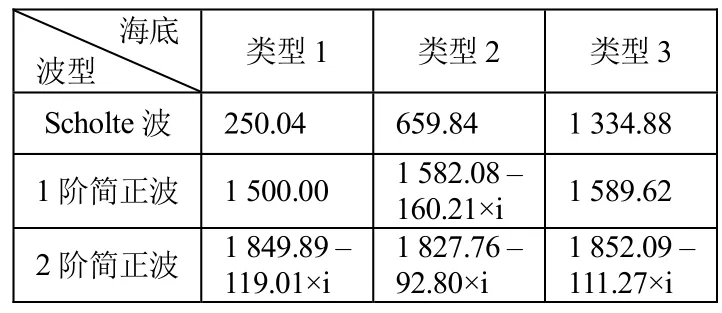
表3 不考虑海底衰减，各类声波相速度值 m/s

不考虑海底衰减时，海底表面声场随距离变化如图1所示。对于1类和3类海底，Scholte波与简正波在传播过程中相互干涉导致加速度产生起伏；对于2类海底，由于不存在波导简正波，Scholte波与衰减简正波相互干涉，因此加速度在近距离上出现相干起伏，远距离只有Scholte波起主要作用，声场变得平缓。从整体趋势上看，垂直加速度值2类海底最大，1类海底最小；水平加速度有类似的规律，只不过1类和3类海底的表面水平加速度值起伏更大。

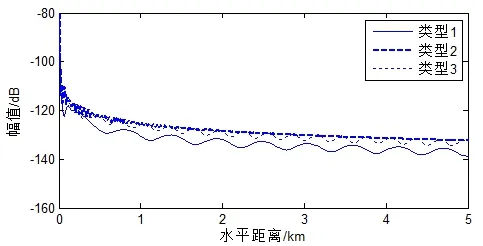
图1 不考虑衰减时，不同海底表面垂直加速度

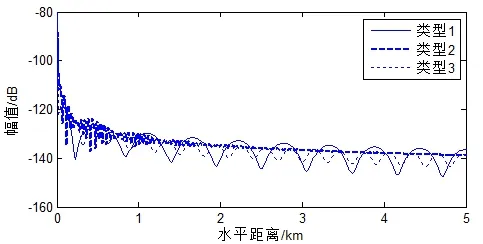
图2 不考虑衰减时，不同海底表面水平加速度

声源频率25 Hz时，考虑衰减的情况下，各类极点值与相速度分别如表4、表5所示。

表4 考虑海底衰减时，各类极点值

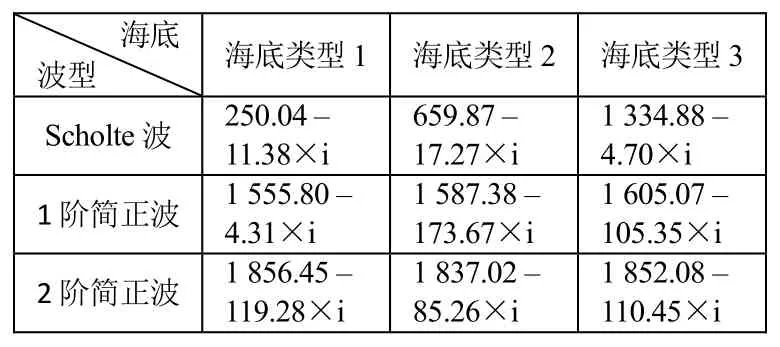
表5 考虑海底衰减时，各类声波相速度值 m/s

考虑海底衰减时，Scholte波和波导简正波的极点均变为复数，说明其在传播过程中随距离衰减。与不考虑衰减时相比，上述所有极点的实部变化不大，说明其相速度变化不大。Scholte极点虚部值在衰减因子较大时也较大，说明衰减因子越大，Scholte波在表面传播时衰减越快。此时简正波均变为衰减简正波，表面声场随传播距离而衰减；原来的波导简正波受海底衰减系数影响较大；原来的衰减简正波极点的虚部变化非常小，说明海底衰减对衰减简正波影响不大。考虑海底衰减时，海底表面声场随距离变化如图3、4所示。由两图可以看出，衰减系数对海底表面声场的影响表现为：随着距离的变远，2类海底表面加速度快速变小，这是因为2类海底情况下激发的是衰减简正波和衰减的Scholte波，在大约1.5 km以内的近距离，二者相干声场出现起伏，1.5 km以外，二者均随距离变大而快速衰减；1类海底表面简正波与衰减的Scholte波在1 km以内互相干涉，1 km以外，受衰减系数影响较小的1阶简正波起主要作用；3类海底表面声场最大，这是由于Scholte波与1阶简正波极点虚部较小，受海底衰减的影响较小，而且在5 km以内均表现为相干起伏的特性。

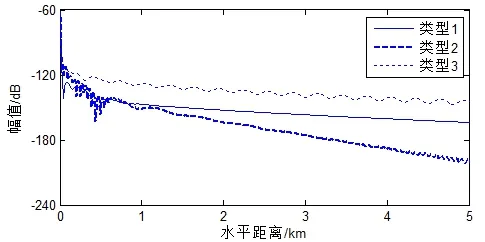
图3 考虑衰减时，不同海底表面垂直加速度

图4 考虑衰减时，不同海底表面水平加速度

声源频率50 Hz时，考虑衰减的情况下，各类极点值与相速度分别如表6、表7所示。与25 Hz情况相比，声源频率为50 Hz时Scholte波的相速度几乎没有变化，说明频率从25 Hz升高到50 Hz时，Scholte波几乎没有频散效应；其极点值变为2倍，说明在相同的水平距离上，Scholte波衰减的速度是原来的 2倍。衰减较小的简正波个数与25 Hz时相比，1类、3类海底由1个变为2个，2类海底由0个变为1个。

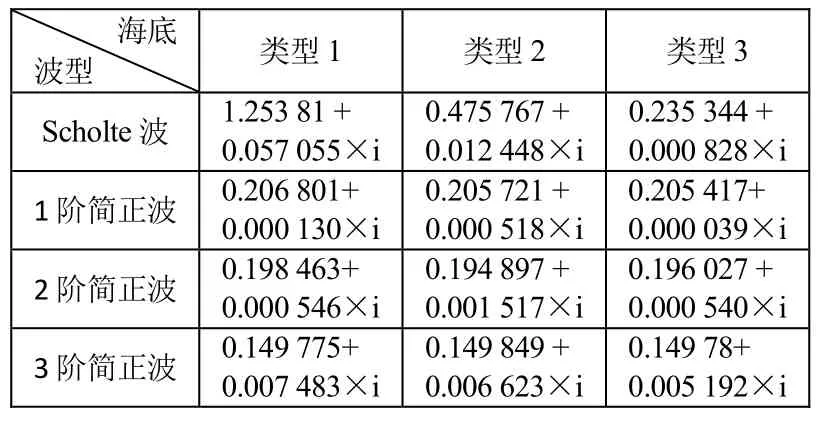
表6 考虑海底衰减时，各类极点值

表7 考虑海底衰减时，各类声波相速度值(m/s)

考虑海底衰减时，海底表面声场随距离变化如图5、6所示。入射波频率50 Hz时海底表面声场整体趋势同样是3类海底最大，2类海底最小；与25 Hz时相比，随距离变远，2类海底表面声场强度下降趋势变缓，这是由于50 Hz时，2类海底激发了衰减较小的简正波。1类、3类海底表面声场随距离的起伏增加，是由相干涉的简正波个数增加所致。

图5 考虑衰减时，不同海底表面垂直加速度

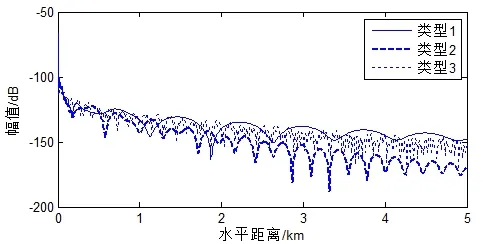
图6 考虑衰减时，不同海底表面水平加速度

3 结论

本文通过求解不同海底类型在有无衰减情况下的极点值，分析了海底衰减对Scholte波、波导简正波、衰减简正波的影响；并采用波数积分方法仿真计算了声源在靠近海底情况下的舰船地震波场，结果表明：

（1）弹性海底情况下，海底表面舰船地震波场中，除了可以激发Scholte波以外还包括简正波，二者的相速度受弹性海底参数的影响。

（2）同一类型弹性海底，衰减系数对各类声波的相速度影响较小，主要是影响声波的衰减；其中Scholte波受衰减系数的影响较大，其次为波导简正波，衰减简正波所受影响较小。

（3）海底存在衰减时，若既存在Scholte波也存在波导简正波，近距离的声场为二者的相干叠加，远距离简正波起主要作用。

（4）对于衰减系数较小的硬质海底（类型3）有利于舰船地震波的探测，其次是非常软的海底（类型1）；若不能产生波导简正波（比如海底类型2，声源频率25 Hz），不利于目标远距离探测。