平和中见关怀，沉稳中显活力，自然中现宗旨

☉浙江省宁波市鄞州实验中学 蔡卫兵

压轴题一般注重考查学生的综合应用能力，往往难度偏大一点，能够使基本功扎实且思维灵活的考生脱颖而出.然而，目前不少中考试卷中的压轴题难度太大，有的方法单一且奇特，有的运算超难，有的分类讨论超繁等，这些压轴题显然压住了考生，只有极少数超优生能够完成，其实它的区分度很小，打“和牌”现象严重，不利于为高中阶段学校招生提供客观、公正的依据.

一、试题及其解答

（1）求直线l的函数表达式和tan∠BAO的值.

（2）如图2，连接CE，当CE=EF时，

①求证：△OCE △OEA；

②求点E的坐标.

（3）当点C在线段OA上运动时，求OE·EF的最大值.

图1

图2

图3

图4

第（2）问第①小题的证法：

证法1：如图3，连接AF.

因为CE=EF，所以∠CAE=∠EAF.

因为AC=AE=AF，所以∠ACE=∠AEF.

所以∠OCE=∠OEA.

又因为∠COE=∠EOA，所以△OCE △OEA.

证法2：如图4，连接FD.

因为CE=EF，所以∠CAE=∠CDF.

又因为∠OEC=∠CDF，所以∠OEC=∠CAE.

又因为∠COE=∠EOA，所以△OCE △OEA.

第（2）问第②小题的解法：

解法1：如图5，过点E作EH⊥x轴于点H.

则25x2-32x+16=4（4-5x），解得，x2=0（不合题意，舍去），则点

解法2：同上得AE=AC=5x，OC=4-5x，CH=x，CE=x.

图5

图6

第（3）问的解法：

解法1：如图6，过点O作OM⊥AB于点M，过点A作AN⊥OF于点N.

由OM⊥AB，AN⊥OF，得∠OME=∠ANE=90°，EN=

解法2：如图7，过点O作OM⊥AB于点M，连接FN.

由EN为直径，得∠EFN=90°.

由于∠OME=∠EFN=90°，∠OEM=∠NEF，则△OME △NFE，则

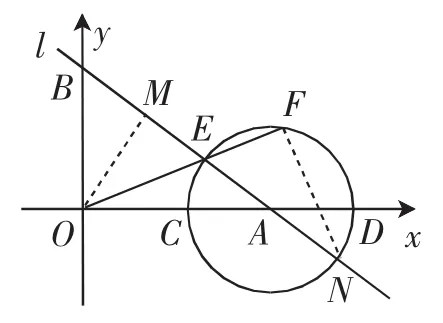
图7

图8

解法3：如图8，连接AF，以O圆心、OE为半径的圆弧交AB于异于点E的G点，作OM⊥AB于点M，则EG=2EM.

解法4：如图9，过点E作EM⊥OA于点M，过点A作AN⊥OF于点N.

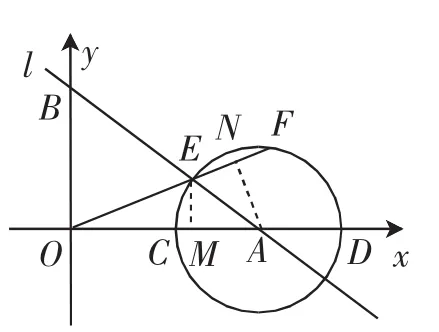
图9

则OE·ON=OM·OA.

二、特色解读

1.平和中见关怀

本题表述简洁，尝试在直角坐标系中加载圆、直角三角形、等腰三角形、相似三角形等元素，涉及的知识有一次函数、锐角三角函数、圆的基本性质、勾股定理等核心知识，并融合运动观点下的函数思想、方程思想、整体思想、从特殊到一般、转化思想等重要思想方法，将重要的数学知识点和数学思维体现得淋漓尽致，但动点的运动路径简单——只在线段OA上，无折线运动；运动速度单一，无速度变化；运动范围明确，满足0＜AC＜；动点引起动圆半径变化，动圆导致交点变化，关联明显清晰，无论是问题背景的呈现还是问题解决的任务，都是熟悉的素材.放低起点、减缓坡度、增加层次，给考生带来希望，不至于望而却步，有助于学生自我潜能的挖掘，使不同水平的考生达到不同的高度，有利于实现“不同的人在数学上得到不同的发展”的评价目标.

2.沉稳中显活力

在以点A为圆心、AC长为半径作⊙A的分析中，最简单、最重要、最基本但又具有特定性质：同圆的半径都相等.在△OCE △OEA的求证分析中，主要是相似三角形中典型的共角共边的母子形，发现随着镜面变化的主动点C和从动点E的变化，在变化过程中有不变的关系∠COE=∠EOA.在CE=EF的特殊条件的分析中，联想到“等弧所对的圆心角相等，圆周角相等，同弧所对的圆周角等于圆心角的一半等有利于解题的信息.结合问题条件和目标，借助等角的补角相等探索出∠OCE=∠OEA或利用圆外接四边形的一个外角等于它的内对角探索出∠OEC=∠CAE.在不增加条件下求点E的坐标，自然再现过点E作x轴的垂线和联系第（1）问中的锐角三角函数和第（2）问第①小题中的相似三角形，由此发展符号意识，用字母表示相关的线段，接着可通过勾股定理列方程，也可利用相似三角形的性质和同一线段的不同表示寻找等量关系，自然、流畅、质朴、和谐，关注过程方法，凸显思维发展.

3.自然中现宗旨

函数是数学学科中最重要、最核心的概念.函数的本质是两个变量之间一种特殊的对应关系.联系和变化是其核心本质.第（3）问求OE·EF的最大值，需要学生具备一定的几何直观、几何推理能力、发现与探究能力、合情推理能力等.立意新颖，构思巧妙，极富创意，蕴含着丰富的数学内涵和思想方法，能很好地反映出学生的数学素养和数学基本功，体现试题的信度和效度.它的求解方法巧妙地避开了通常求最值的问题，转为深入挖掘隐含的数量关系，进而通过建立变量之间的函数关系求解，而这又何尝不是求最值的通性通法？同时解题途径宽，可作弦心距来处理与弦有关的问题而构造分别包含线段OE、EF的直角三角形相似；也可见直径找直角来处理与弦有关的问题而构造分别包含线段OE、EF的直角三角形相似；也可连接圆上点与圆心而构造分别包含线段OE、EF的等腰三角形相似；也可将前面已经获得的解题经验和过程结论信息集中优化分析而构造A型相似，得到与主动点C运动到不同位置时的横坐标或纵坐标或动圆半径之间的一次函数关系，进而通过整体代入得到OE·EF与自变量x之间的二次函数关系，这样兼顾不同水平考生，让学生更多地关注基本图形，挖掘其本质特征，体会“变中有不变”，在能力立意的基础上进一步体现素养立意.

三、教学导向分析

《义务教育数学课程标准（2011年版）》指出：数学课程内容“不仅包括数学的结果，也包括数学结果的形成过程和蕴含的数学思想方法”.对于第（2）问第①小题，以相似三角形和圆等核心知识交汇为背景，蕴含了逻辑推理、直观想象等素养的要求，第②小题渗透着联系的观点与方程思想，自然生成，顺势而为.从第（2）问到第（3）问，凸显运动的观点与从特殊到一般的数学思想.第（3）问线段之积的最值又蕴含着函数思想、转化思想、整体思想，点C的运动范围满足引领着极端思想和分类讨论思想的催生，点在线段OA上运动，当时，OE与⊙A相切，当时，点F在线段OE上，可以体现数学试题的深层次思维.所以我们要善于在知识的交汇处，以基础知识与基本结论为载体，关注学科本质，注重通性通法，淡化特殊技巧，基于知识转化，探求以题会类，循序渐进地引领学生的思维能力发展，在恰当的时机提炼，用接地气的语言概括，让隐性的思想方法浮出水面.从本质上讲，会用数学的眼光观察现实世界（数学抽象、直观想象）、会用数学的思维思考现实世界（逻辑推理、数学运算）、会用数学的语言表达现实世界（数学建模、数据分析），是超越具体教学内容的数学教学目标，其中“四基”是发展学生核心素养的有效载体.素养的形成，不能单纯依赖教师的教，还需要学生参与其中的数学活动；不能单纯依赖记忆与模仿，还需要感悟与思考.因此，基于核心素养的教学，要求教师抓住知识的本质，创设合适的教学情境，启发学生思考，让学生在掌握所学知识和技能的同时，感悟知识的本质，积累思维和实践的经验，最终形成和发展数学核心素养.