大型会议筹备的最优方案决策

宋军智 何娟 陈鑫 周俊

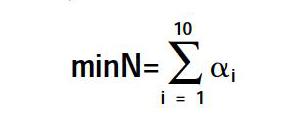
[摘           要]  在会议如潮的当下，各种全国性、国际性的大型会议越来越多。作为会议筹备组，一个合理的最优会议筹备方案格外重要。通过一元线性回归预测出实际与会人数，在此基础上建立多目标优化模型，通过分层的方式将多目标优化模型转化为单目标优化模型，进一步利用LINGO软件求解得到会议筹备的最优方案。

[关    键   词]  线性回归;多目标优化;会议筹备

[中图分类号]  C931.47               [文献标志码]  A              [文章编号]  2096-0603（2019）31-0088-02

交流产生灵感，碰撞产生火花。在各行各业快速发展的背景下，各种大型交流会议应运而生。作为会议筹备组面临的问题也日趋复杂，主要涉及会议召开时间、会议召开地点、会议召开主题、参会代表食宿等问题的安排。作为会议承办方首要考虑因素为自己的效益最大化，但同时要考虑到满足参会代表诸如房间类型、房间价格、便利程度等要求，以提高参会代表满意度。本文以2009年全国大学生数学建模竞赛（CUCM）题目D题中的相关数据为背景，建立一个以经济、方便、代表满意为目标的优化模型，以此制定预定客房、租借会议室、租用客车的最优会议筹备方案。

一、实际与会人数的预测

根据往届会议回执的统计数据表明，存在部分代表发了回执但未参会或参会代表未发回执的情况。为了合理地预定客房，根据往届回执情况统计数据利用线性回归进行预测，再结合本届会议发来回执的代表数据便可得到本届会议的实际与会人数。

计算公式如下：

y=y0-y1+y2

其中，y0为本届会议发来回执人数;y1为本届会议发来回执但未与会的预测人数;y2为本届会议未发回执确参会的预测人数。

（一）利用往届回执情况数据绘制散点图

绘制以X轴为发来回执的代表数量，Y轴为发回执未与会代表人数的二维坐标散点图，如图1。

绘制以X轴为发来回执的代表数量，Y轴为与会代表未发回执数量的二维坐标散点图，如图2。

（二）一元一次函数建立

由于两个散点图像特点均符合线性函数，可利用线性回归对其进行线性拟合，建立一元一次函数：

y2=a1x+b1+c1

c～N（0，σ^2）

通过matlab计算得到，“与会未发回执的代表数量随着发来回执代表数量”线性关系为：

y1=0.300x+0.459（拟合优度R2=0.725，拟合程度好）

同理，未发回执而与会的代表数量随着发来回执代表数量的线性关系为：

y2=0.109x+27.42（拟合优度R2=0.702，拟合程度好）

（三）一元一次函数求解

带入本届回执数据后得到y1≈227，y2≈115，y=657。即本届与会总人数为657。

二、最优会议筹备方案的模型建立

（一）决策变量的确定

作为会议筹备组，首先要解决的问题是从备选宾馆中确定要预定的宾馆，并在此基础上确定宾馆房间的预定、会议室的预定、客车类型与数量的预定。為得到一个完整合理的会议筹备方案，本文以xij，yij，si为决策变量，其中xij表示第i个宾馆第j种类型的房间数量，yij表示第i个宾馆第j种会议室的数量，si表示租用第i种类型的客车数量。

（二）优化目标的确定

优化目标一：宾馆的数量最小

为了方便会议的顺利召开，作为会议筹备组，在条件允许的情况下，应尽可能地使参会代表更集中，因此建立以预订宾馆数量最少为目标的目标函数：

（四）多目标优化模型的确立

综上建立一个以minN，minL，minH，minK为目标的多目标优化模型：

三、最优会议筹备方案的模型的求解

针对以上多目标优化模型，由于对各个目标直接加权没有实际意义，因此采取分层转化为单目标优化问题进行求解。通过对各个目标重要程度加以区分，选择宾馆数量最少作为第一层目标，会议室费用最小作为第三层目标，租车费用最少作为第四层目标，分层后得标，距离最短作为第二层目标相应的模型为：

分别将上一层的求解结果作为下一个模型的约束条件，便可得到新的单目标优化模型。在此，受限于篇幅的限制，另外三个模型不一一赘述。

由于以上4个模型最终都为单目标线性规划模型，可直接采用LINGO求解。求解结果为：会议筹备方应预定2号宾馆107间，10号宾馆22间，6号宾馆40间，7号宾馆120间，8号宾馆125间;预定会议室2号宾馆130人规模1间，7号140人宾馆2间，200人宾馆1间，8号宾馆130人规模2间;租赁33座客车13辆，45座客车1辆;宾馆距离最短7200米，共将花费10400元。

本文针对一个实际的会议筹备案例，给出了从数据准备、模型建立到模型求解的完整解决过程。对解决类似的问题有一定的参考和借鉴价值。

参考文献：

[1]全国大学生数学建模竞赛组委会.2009高教社杯全国大学生数学建模竞赛（CUCM）题目D题.http：//www.mcm.09/problems2009C.asp.

[2]尹川，刘润，白云强.数学建模在会议筹备工作中的应用[J].太原师范学院学报（自然科学版），2012（4）：78-81.

[3]阮晓青，周义仓.数学建模引论[M].北京：高等教育出版社，2005.

编辑 尹 军