Nekrasov矩阵线性互补问题误差界的估计

李艳艳

（文山学院 数学与工程学院，云南 文山 663099）

线性互补问题（Lcp (M,q)）广泛应用于二次规划、双矩阵对策、期权定价问题等交通、经济和控制等领域[1-4],它的模型是指求x∈Rn，满足

其中M是实矩阵，q是实向量。

当线性互补问题中所定义的M矩阵具有较好的性质时，它的求解将会容易许多，例如当M是主子式都为正的实矩阵（P矩阵）时，该问题不仅有唯一解，且能较容易的得到误差界[5]。

例如，陈小君等在文献[6]中给出了P矩阵线性互补的误差界

r, 在该误差界问题中，最难求的是，关于该难点，最近几年许多学者在文献[7-9]中进行了大量的研究。

本文将研究主对角元素为正的Nekrasov矩阵的线性互补误差界估计问题，通过利用Nekrasov矩阵逆的无穷范数上界的估计式，结合它的性质和不等式性质，给出该问题的一些新估计式。

1 预备知识

设矩阵M= (mij)∈Cn×n（Cn×n为复矩阵集），对∀i∈N， 有，称M是Nekrasov矩阵。

关mii＞ 0的Nekrasov矩阵的线性互补误差界估计问题. 李朝迁，高磊分别在文献[10-11]中给出下面的两个估计式

引理 1[10]设M= (mij)∈Cn×n是mii＞0 的 Nekrasov矩阵，令0≤di≤1，则是Nekrasov矩阵，进一步，对任意的

引理 2[12]设γ＞0,η＞0，则∀x∈[0,1]有

引理 3[10]设M= (mij)∈Cn×n是mii＞0 的 Nekrasov矩阵，令

引理 4[13]设矩阵A=(aij)∈Rn×n是 Nekrasov 矩阵，若

则

引 理 5[13]设 矩 阵A=(aij)∈Rn×n是 Nekrasov 矩阵，若

则

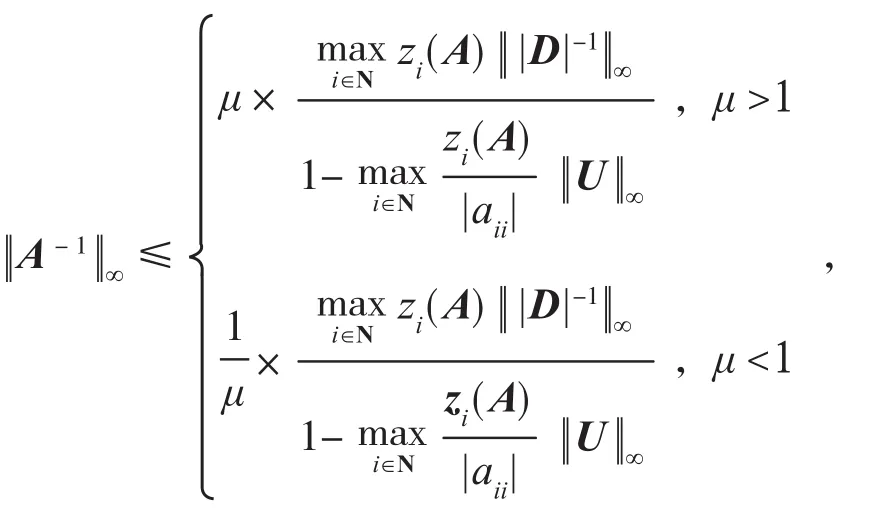
2 主要结果

本部分给出对角元素为正的Nekrasov矩阵的线性互补误差界估计式。

定理 1设M= (mij)∈Cn×n是mii＞0 的 Nekrasov矩阵，，则

证明：设0≤di≤1，则由引理1知是Nekrasov矩阵，应用引理2中的不等式和zi(M)，ηj(M)的关系得

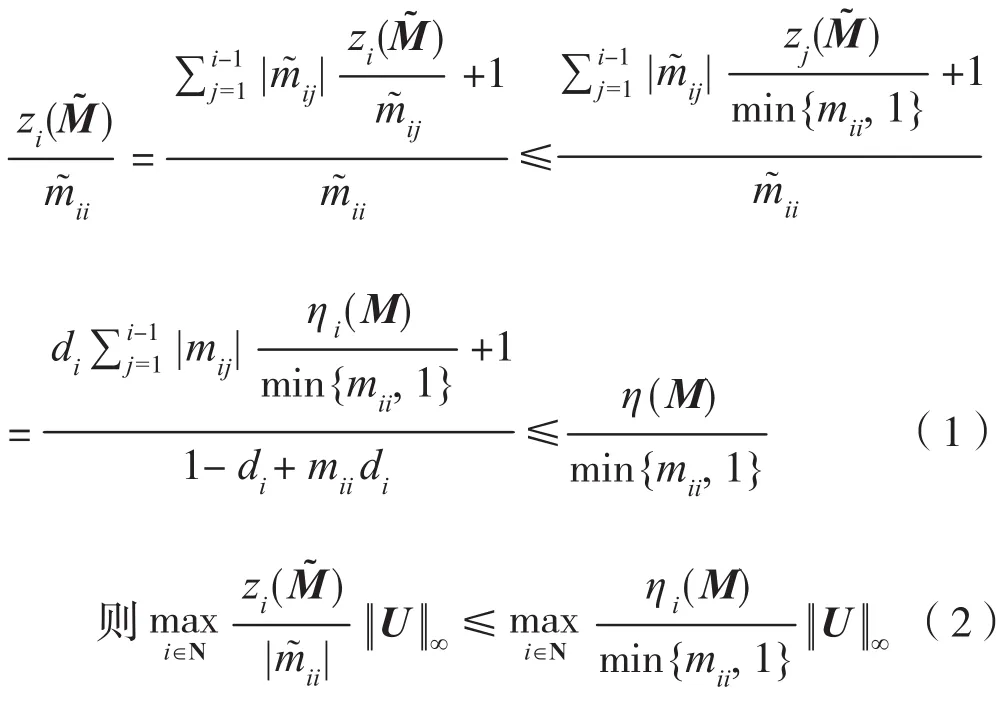
应用引理4中Nekrasov矩阵逆矩阵无穷范数的估计式和（1），（2）式知下面的结果

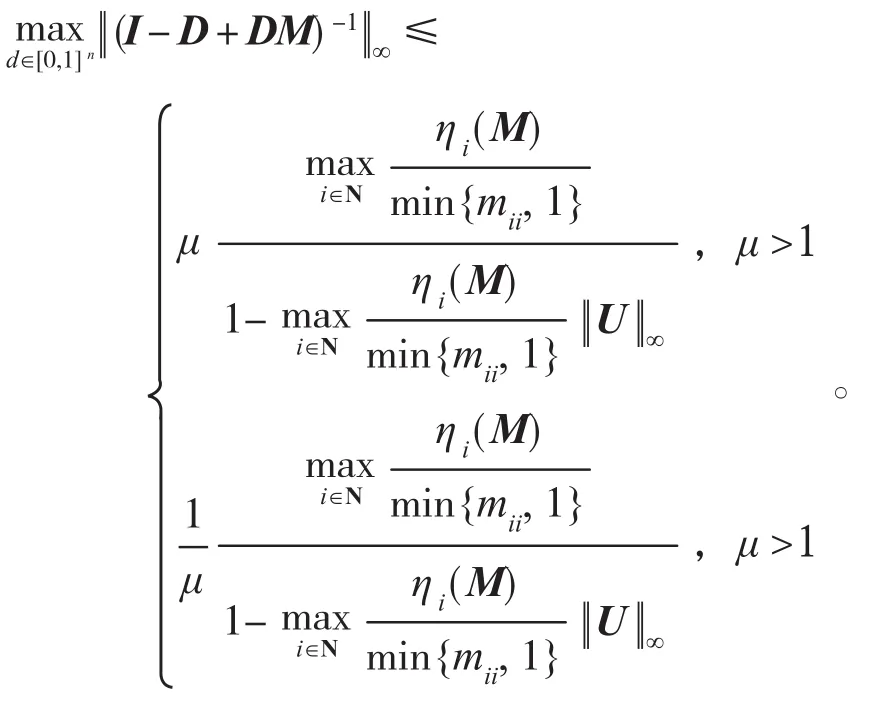
定理证毕。

定理 2设M= (mij)∈Cn×n是mii＞0 的 Nekrasov矩阵，，则

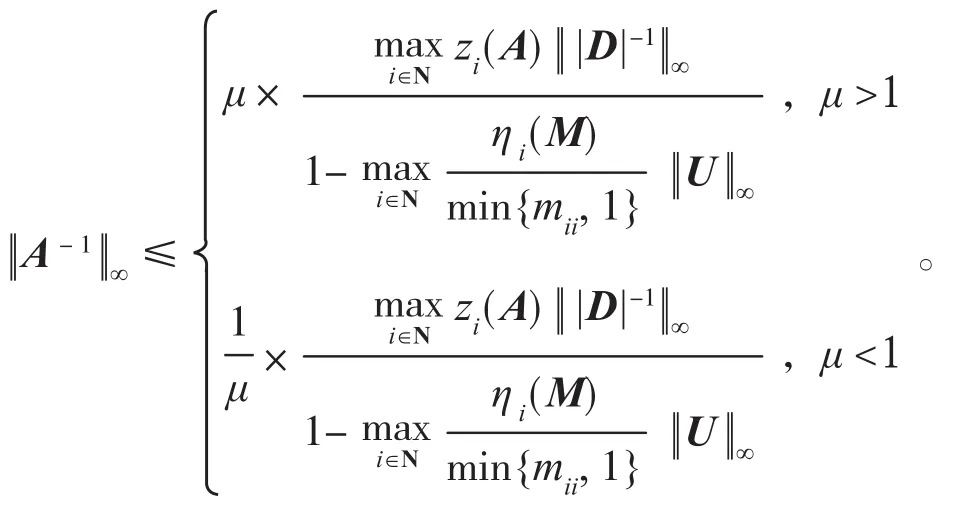
证明：设0≤di≤1，则由引理1知是Nekrasov矩阵，应用定义和不等式的性质得

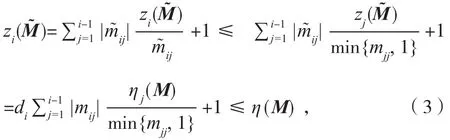
由定理1的证明知

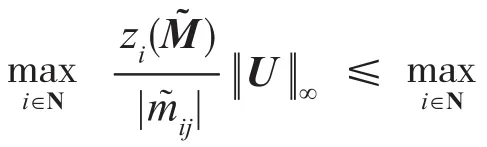
应用引理5中Nekrasov矩阵逆矩阵无穷范数的估计式和（3），（4）式知下面的结果

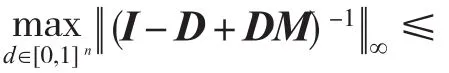
3 数值算例

应用本文定理1中的估计式，当μ取不同值时的结果见表1。

表1 μ取不同值时的结果