情境问题与数学知识的相融性探究

□胡连成

（丰县华山初级中学，江苏丰县 221744）

问题情境是指与教学目的、内容、学生认知结构相关，能激起学生发现问题、提出问题，使其进入思维、探究的思想状态的外部环境.把学生置身于研究新的未知的问题情境，让学生感到问题既熟悉又陌生，不能单纯利用已有的知识和方法去解决，产生认知的困惑，在“悱、愤”中发现新问题、激发探索欲望、在探索中收获知识与经验，在思考中感悟思想与方法.

数学知识的学习需要在解决问题中实现，数学知识的探索需要情境的渲染与引领，数学学习能否吸引学生，需要教师精心设计问题情境，使其具有引人入胜的情境、诱人探索的问题、促人深思的内涵，以实现在探索中提高学习能力，在思考中发展数学思维的教育目的.本文结合实例阐述问题情境在数学教学中的引领、启发与提升作用.

一、在情境引入中引领知识探索

阿基米德曾经说过：给我一个支点，我可以撬动地球.同样教师也可以说：给我一个支点，我可以玩转课堂.阿基米德的支点在哪里？我们不知道.但课堂教学的支点是可以确定的，那就是学生的求知欲和好奇心.通过精心设计数学情境，唤醒学生的问题意识，激发求知欲望，点燃思维火花，引领学生走向忘我的学习境界.

案例1“圆周角定理”的引入

2015年2月27日，我国审议通过了《中国足球改革总体方案》，从国家层面明确了足球的战略意义.我校响应号召，组建了足球队.在足球比赛场上，甲、乙两名队员互相配合向对方球门MN进攻.当甲带球到A点时，乙随后冲到B点，如图1所示.

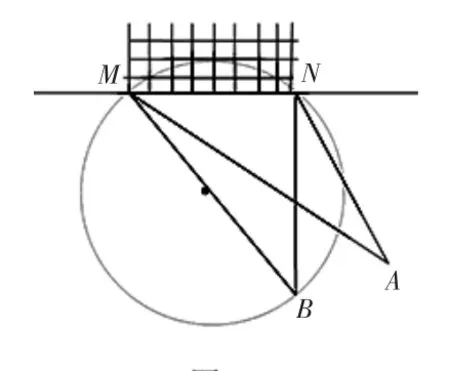
图1

问题1：此时甲是自己直接射门，还是迅速将球回传给乙，让乙射门，更容易进球呢？（不考虑其他因素）

问题2：请度量∠MAN，∠MBN的度数，这时是甲自己直接射门，还是迅速将球回传给乙，让乙射门，更容易进球呢？

问题3：如果乙队员的站位在优弧MN的其他位置时，你的判断是什么？

问题4：如果乙队员沿着优弧MN上路线跑动时，∠MBN的度数是否发生变化？你能解释其中的原因吗？

【案例点评】以校园足球队的射门角度设计情境，看似平常现象却隐含丰富的数学知识，通过有趣的问题引发学生的思考，体现“现实性、趣味性和数学一致性相统一”[1]的情境设计基本原则.在有趣的情境中通过问题1的直观猜想引起学生进一步思考“为什么是这样”.再通过度量操作、位置变化等数学活动，把现实问题自然转化为思考有关“圆周角”的数学问题，“知其然更要知其所以然”.让学生经历从猜想到验证、从操作到推理的探索过程，从具体问题情境出发建立数学模型，把实际问题转化为数学问题，通过解决数学问题进而解决实际问题，这种历程对于发展学生从数学的角度思考问题、运用数学方法解决问题具有十分重要的意义.

二、在知识探索中思考数学本质

美国心理学家布鲁纳曾指出：教学过程是一种提出问题和解决问题的持续不断的活动.在教学活动中，教师要充分关注学生的学习过程，善于创设探究情境，给学生提供思考的空间和实践的机会，使学生在不断的情境探索活动中收获经验、归纳规律、发展数学思维.

案例2底部不可到达的测量问题

苏科版义务教育教科书《数学》九年级下册第7章第6节“用锐角三角函数解决问题”第三课时情境案例如下.

小明在某处利用测角仪观测气球的仰角（从低处观测高处的目标时，视线与水平线所成的锐角）为27°，然后他沿正对气球方向前进了50m，此时观测气球的仰角为40°（见图2）.如果测角仪高度为1m，那么气球的高度是多少？

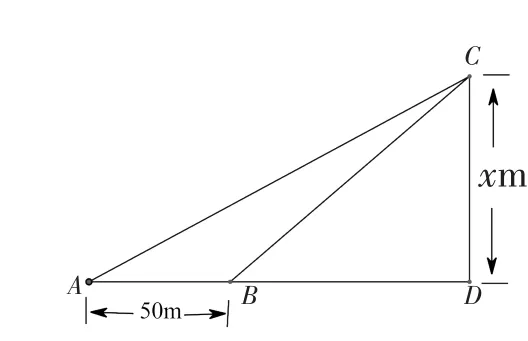
图2

结合教学实际，对教科书的情境案例进行了如下改动.

问题1：小明在A处利用测角仪观测气球的仰角为30°，然后他沿正对气球方向前进了50m到达B处，此时观测气球的仰角为60°.如果测角仪高度为1m，那么气球的高度是多少？

问题2：小明在A处利用测角仪观测气球的仰角为30°，然后他沿正对气球方向前进了50m到达B处，此时观测气球的仰角为45°.如果测角仪高度为1m，那么气球的高度是多少？

问题3：小明在A处利用测角仪观测气球的仰角为α°，然后他沿正对气球方向前进了am到达B处，此时观测气球的仰角为β°.如果测角仪高度为bm，那么气球的高度是多少？

问题4：小明在A处利用测角仪观测气球的仰角为30°，然后他沿正对气球方向前进了50 m到达B处，此时观测气球的仰角为75°.如果测角仪高度为1m，那么气球的高度是多少？（结果保留根号）

【案例点评】本案例采取了“逐步深入、归纳规律、灵活运用”的思路对问题情境进行变式的拓展.问题1根据角度关系求出线段BC，进而解Rt△BCD求出线段CD的长度.问题2需要利用“设未知数、解方程”的方法求线段CD的长度.问题3进一步思考了“用字母探寻一般规律”的数学模型.问题4根据“结果保留根号”的要求，跳出前面总结的数学模型的束缚，灵活运用知识，过点B作△ABC的高，构造3个含特殊角的直角三角形解决问题.这一系列的情境问题串的变式探索，引领学生感悟数学建模和方程思想，发展数学辩证思维能力.“具体结论”上升为“普遍规律”，复杂多变的现实问题才能呈现简洁的数学美.灵活运用数学规律从不同角度解决问题，数学知识才能焕发七彩光芒，学生对数学知识方法与思想的理解才能更全面而深刻.所以问题情境的探索不要局限于一个具体问题，而要在思考一系列的问题串过程中有所思、所想、所获，这才是情境教育的理想目标.

三、在知识归纳中提升能力

数学知识学习，贵在“通透融合”.“通”为互通，知识点融会贯通、四通八达、形成体系；“透”指透明，知识点本质要义一目了然、熟烂于胸[2].数学教学需要处理好局部知识的学习和整体知识融合，达到“既见树木又见森林”的目的，形成完整的知识体系和方法思想的领悟.这一切的实现可以通过教师精心设计问题情境，让学生在不断的问题探索中归纳数学方法、构建知识体系、感悟数学思想、提升学习能力.

案例3探索三角形中的特殊点

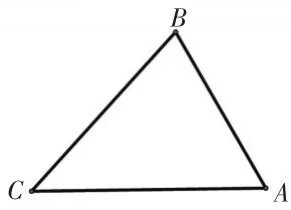
图3

有三个村庄A，B，C，相互之间有笔直的道路连接（见图3）.现需要在三角形区域内建一所仓库.为了方便与三个村庄的货物运输，请你结合所学数学知识，提出有关仓库选址的问题，并尝试进行解答.

学生根据所学知识，提出很多问题.笔者选择以下6个问题，进行讨论和交流.

问题1：要使仓库到三条道路的距离相等，那么仓库应选在何处？

问题2：要使仓库到三个村庄的距离相等，那么仓库应选在何处？

问题3：要使仓库到三条道路的距离相等，且到三个村庄的距离也相等，那么仓库应选在何处？

问题4：要使仓库到三个村庄的距离和最小，那么仓库应选在何处？

问题5：要使仓库到三条道路的距离和最小，那么仓库应选在何处？

问题6：如果仓库与A，B，C三个村庄的货物的流通量的比例是1∶2∶3，那么仓库应选在何处，有利于货物流通？

【案例点评】本案例是在学生已经学习了三角形的内心和外心的基础上进行的一节复习课的情境设计.通过仓库的选址情境，引发学生从不同角度思考问题.

问题1和问题2涉及三角形的内心、外心知识.学生已经学习了相关内容，可以较好地给出解决方案.问题3需要思考只有等边三角形的内心和外心才能互相重合，结合正多边形与圆的关系进行分析.正确把握三角形的内心、外心、重心、中心（等边三角形）之间的联系和区别，形成完整的知识结构.

问题4提出的“到三角形三个顶点距离和最短的点”称作“费马点”.它最早是17世纪法国数学家皮埃尔·德·费马提出的.具体内容是：①当三角形3个内角均小于120°时，那么三角形内存在到三顶点形成的夹角均为120°的点，这个点到三顶点的距离和最短.具体方法如下：如图4，点O为△ABC内任意一点，连接OA,OB,OC，把△OCB绕点C逆时针旋转60°得到△O′CB′，则OA+OB+OC=OA+B′O′+OO′，当点A,O,O′,B′四点共线时，即把线段OA,OB,OC转化为一条线段时，点O到三顶点的距离和最短，这时∠AOB=∠BOC=∠AOC=120°.②当三角形有一内角大于或等于120°时 ，如 图 5，∠ABC=120°，OA+OB+OC=OA+B′O′+OO′＞AB+BB′，所以，此钝角的顶点就是到三顶点距离和最短的点.

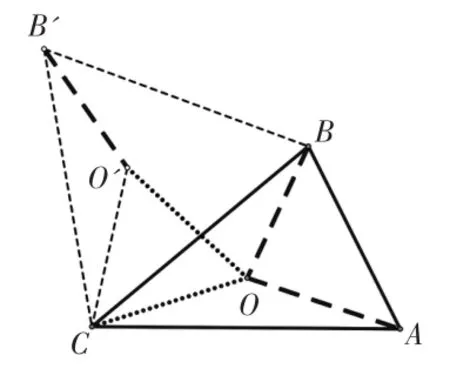
图4

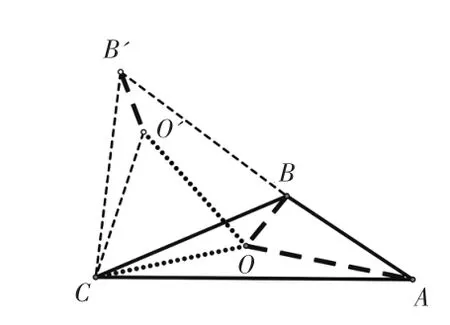
图5

问题5提出的“在三角形内到三边距离和最短的点”也是存在的，具体结论如下：对于一般三角形而言，到三边距离和最短的点位于最大角的顶点处.

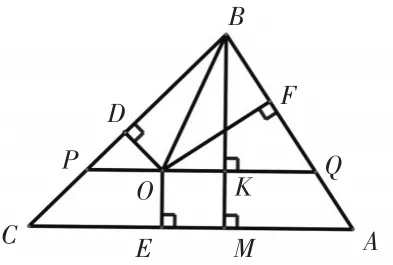
图6

如图6，在△ABC中，AB＜BC＜AC.点O为△ABC内任一点，OF⊥AB，OD⊥BC，OE⊥AC，垂足分别为点F,D,E.过点O作平行于AC的直线分别交AB,BC于点Q,P.BM⊥AC于点M,交PQ于点K.

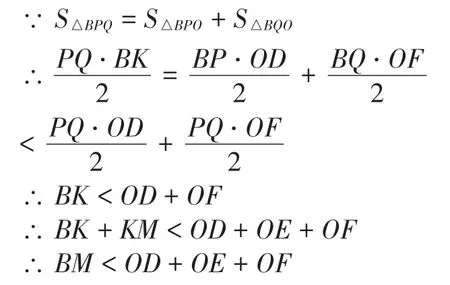
根据AB＜BC＜AC，可知BM为△ABC中最短的高.所以，不等边三角形的最大内角的顶点到三边的距离和最短.两类特殊情况：①腰长大于底边的等腰三角形，底边上任意一点到三边距离和相等，且到三边距离之和最小；②等边三角形内（包括三边）的任意一点到三边距离和是相等的，没有长短之分.

对于问题6需要结合货物的流通量的比例进行最优化方案设计.由于问题复杂，学生思考会具有很大的挑战性，暂时无法解决，但它像一颗种子一样，深深扎根于学生的心田，启发、引领学生思维的发展，总有一天会绽放美丽的花朵.

初中阶段学生主要学习了三角形的内心、外心和重心，对于三角形的垂心以及本文探索的“费马点”和“到三边距离之和最短的点”初中阶段鲜有涉猎.对于这六个和三角形有关的特殊点，如果从联系的观点去思考，可以发现它们殊途同归，聚合于正三角形，和谐而美妙，形散而神聚，最终统一于正三角形的中心.进一步思考，对于四边形而言，是否也有类似的特殊点，它们是否也统一于正四边形的中心呢？五边形呢？……n边形呢？丰富多彩的问题现象蕴含着的数学规律，永远是那么的简洁而和谐.从问题1到问题5，从问题2到问题4，最终拓展到问题6，在情境的渲染引领下，实现思维方式从静态思考到动态思维的转变，知识结构从单个知识点到纵横知识网的深度拓展.通过一个情境引发一串问题，灵动而深邃.带着问题走入课堂，带着新问题走出课堂，让问题引领思维发展，这正是情境设计所要到达的效果.“情境”与“问题”二者犹如土壤与花朵，“情境”如果是肥沃土壤，“问题”就是盛开的花朵，思想与方法就是收获的累累硕果，过程与经验就是静待花开的磨砺，核心素养就是潜移默化的升华.

情境之于知识，犹如汤之于盐.盐需溶入汤中，才能被吸收；知识需要溶入情境之中，才能显示活力和美感.那么，情境在学习中的作用是什么呢？是对兴趣的激发、探索的引领、思想的感悟.在精心设计的数学情境氛围渲染下，激发学生的问题意识，以问题探索引领知识学习.融知识于情境，蕴思想于探索，在积极的情境探索中，实现知识的融汇、能力的提升.