深空通信载波同步高精度FFT频偏估计算法

王翠莲 李寅 禹霁阳 李珂

(1 北京空间飞行器总体设计部，北京 100094)(2 航天东方红卫星有限公司，北京 100094)

深空通信信道存在对地通信传输时延大，信道信噪比极低，通信距离远，通信环境变化大等特点。特别在火星探测器设计中，进入、下降与着陆(EDL)阶段对地通信信道具有高动态、低信噪比的特点，需选用合适的信号调制技术降低解调的难度，保证EDL过程中正常通信[1]。目前深空探测器应答机设计中通常采用多进制相移键控(Multiple Phase Shift Keying, MPSK)作为调制方式实现远距离的可靠通信。MPSK信号在解调时，需要将载波频率、相位通过一定的映射关系获得解调结果，因此获得精确的载波同步尤为重要。在传统的探测器应答机设计中，一般采用锁相环算法实现载波捕获和跟踪。在采用MPSK调制且信噪比低于6 dB时，锁相环失锁现象明显，无法可靠工作[2]。因此，基于频偏估计的载波同步开环算法成为深空通信的研究热点。

现有的频偏估计算法基本是建立在求解最大似然方程的基础上。一般有两种思路：第一种是利用输入序列的自相关函数构造频偏估计量，如L&W算法[3]、Fitz算法[4]以及M&M算法[5]等；第二种是用快速傅里叶变换(Fast Fourier Transform, FFT)作周期图，然后搜索周期图的峰值位置，利用频偏值和峰值位置的对应关系求解[6]。周期图法的优点是能直接检测频偏的绝对值，同时估计速度较快，但其固有的缺点是，用于估计的序列长度直接影响估计的精度，并且存在一定的信噪比门限。在估计序列长度一定的前提下，该方法需要在获得初始FFT峰值谱线位置后进行插值[7-10]以提高频率分辨率。本文提出的算法只需进行一次插值即可获得频偏的无偏估计值。在低信噪比条件下，插值算法在某些频点估计精度不够高，因此在插值后进行二分搜索，二分搜索的次数取决于估计精度要求以及硬件实现复杂度。

1 系统模型

在深空探测器应答机设计中，采用开环算法的数字解调软件由数字下变频、捕获、位同步、载波同步、解调、译码几个部分组成，详见图1。模/数转换器(Analog-to-Digital, ADC)采样后的中频信号经过数字下变频后输出零中频低速信号。位同步模块通过位定时误差估计和补偿获得最佳采样点信息。载波同步模块包括频偏估计和频偏补偿两部分，载波同步后的信号进行后续的MPSK解调及译码。

位同步完成后，包含数据信息和载波频偏、相偏的MPSK信号可表示为

rn=ej(2πΔfTn+φn+θ)+vn

(1)

式中；rn为位同步后的数据序列的第n个符号；Δf为收发载波间的频偏；T为码元周期；vn为加性复高斯白噪声；θ为收发载波的初始相偏；φn为数据调制的相位。

在频偏估计前，首先去除rn中的调制信息，得到包含加性噪声的单载波信号hn。帧头数据对于接收端是已知的，故有

(2)

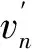
假设帧头长度(即用于估计的序列长度)为N，对hn做N点离散傅里叶变换，可以得到其频谱

(3)

式中：k=0,1,…,N-1。在获得的N条谱线中搜索kmax，使|Fk|值达到最大，根据最大似然估计理论，频偏Δf的最大似然估计表达式为[7]

(4)

当FFT长度为N时，算法可估计的最大及最小频偏分别为

(5)

由式(5)可知，FFT算法理论上可以达到的频偏估计范围是-0.5fs～0.5fs(fs为码元速率)。

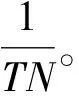
(6)

理论上，FFT序列长度N的增加能够线性的减小估计误差，但在深空探测器应答机设计中，由于信道资源有限，为提高传输效率，N的取值一般不超过256。当系统要求的同步精度较高时，算法的估计误差不能容忍。因此，必须设法减小FFT算法引入的估计误差。常用的提高FFT算法估计精度的方法是基于插值的思想，如抛物线插值算法[7]、Rife插值算法[8]、Jacobsen算法[9]、Quinn算法[10]等，这些算法都是频偏的最大似然估计值在理想情况下的近似。本文采用的插值算法经过一次反正切运算即可获得插值量，可以显著的提高估计精度。

2 基于插值的粗估计

假设FFT得到的初始峰值谱线位置为kmax，实际的峰值位置分布在(kmax-1)和(kmax+1)之间，因此只需在(kmax-1)和(kmax+1)之间进行插值。由式(3)、式(4)，可得

(7)

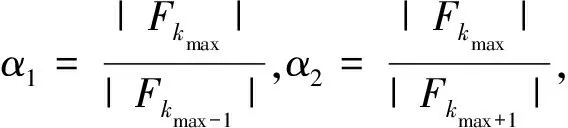
(8)

推导可得

(9)

式中:

(10)

与式(4)比较，相当于用η修正初始的峰值谱线位置，Δf的估计值为

(11)

为便于进行性能比较，此处列出抛物线插值方法、Rife插值算法和Jacobsen差值算法的修正值η1、η2和η3，分别为[7-9]

(12)

式中：|Fksec ond|是|Fkmax+1|和|Fkmax-1|中较大的一个，Re[ ]为取实部运算。

3 基于二分搜索的精估计

基于插值的FFT频偏估计存在一个固有的问题，在低信噪比条件下进行插值时，α1、α2大小可能出现误判。特别是在实际频偏值接近峰值谱线时，估计结果偏差较大，因此需要在插值基础上进行二分搜索以获得更精确的频偏估计值。

由式(11)获得频偏粗估计值对应的频点δ0=kmax-η，在区间[δ0-ε,δ0+ε]进行搜索。假设

(13)

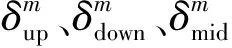
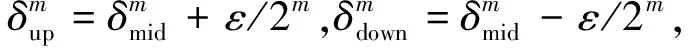
(14)

对搜索迭代次数m的选取，需要兼顾系统需要达到的频率精度以及实现复杂度。算法精度由归一化估计方差表示，搜索次数m与算法精度的关系为

(15)

4 算法性能仿真

在深空探测器应答机设计中，频偏估计算法的精度决定了载波同步准确度和载波同步门限，直接影响解调误码率和解调门限这两项关键的应答机解调性能指标。本文设计仿真程序对算法的估计精度进行了评估。

FFT频偏估计算法的估计误差是一个随实际频偏值成周期变化的函数，周期为FFT的频率分辨率，即两根相邻谱线之间的距离。仿真环境设定如下：①采用MPSK调制方式；②估计序列长度为N=256；③码元速率fs为300 kHz，采样频率2400 kHz；④频偏的变化范围为距离谱线位置偏移量[-0.5,0.5]的区间；⑤采用平方根升余弦滤波器；⑥二分搜索区间ε=0.1。

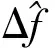
(16)

式中：Es/N0为信号能量与噪声能量比。

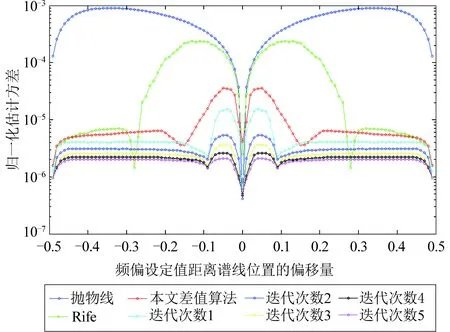
图2 算法估计精度比较Fig.2 Comparison of estimation accuracy

图2中横轴表示频偏设定值距离谱线位置的偏移量，偏移量为0.5时即为两根谱线的中间位置。从图2中可以看出，抛物线插值算法在实际频偏接近FFT的离散谱线位置时，插值效果明显，但在实际频偏远离FFT的离散谱线位置时，插值效果并不明显；Rife插值算法性能优于抛物线插值算法，但在实际频偏接近FFT的离散谱线位置时频偏估计结果偏差较大；本文提出的插值算法性能优于抛物线差值算法和Rife插值算法，但在对估计精度要求高的场合，仍需采用二分搜索方法进一步提高估计准确度。随着二分搜索迭代次数的增多，估计精度逐渐提高，尤其是在靠近离散谱线位置。当搜索迭代次数等于5时，整个频偏估计范围内的精度估计接近CRB。

在深空探测器应答机设计中，用于载波同步的估计序列长度N一般为64、128、256。为进一步验证算法的抗噪声性能，仿真了不同估计序列长度，不同信噪比条件下的归一化估计方差。信噪比的变化范围为-16～12 dB；设定初始频偏值在距离谱线位置偏移量[-0.5,0.5]的区间内随机分布。由图3～图5可知，几种算法估计频偏都存在信噪比门限，即当信噪比低于该值时，估计性能急剧恶化。N为64、128、256时，对应的信噪比门限分别约为-2 dB，-5 dB、-8 dB。

图3 算法估计精度与CRB比较(N=256)Fig.3 Comparison of estimation accuracy with CRB (N=256)

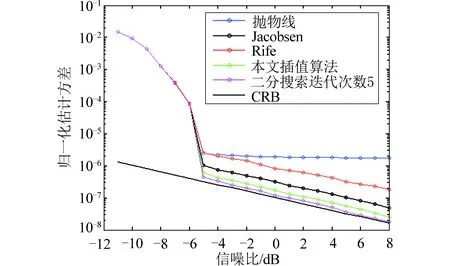
图4 算法估计精度与CRB比较(N=128)Fig.4 Comparison of estimation accuracy with CRB (N=128)

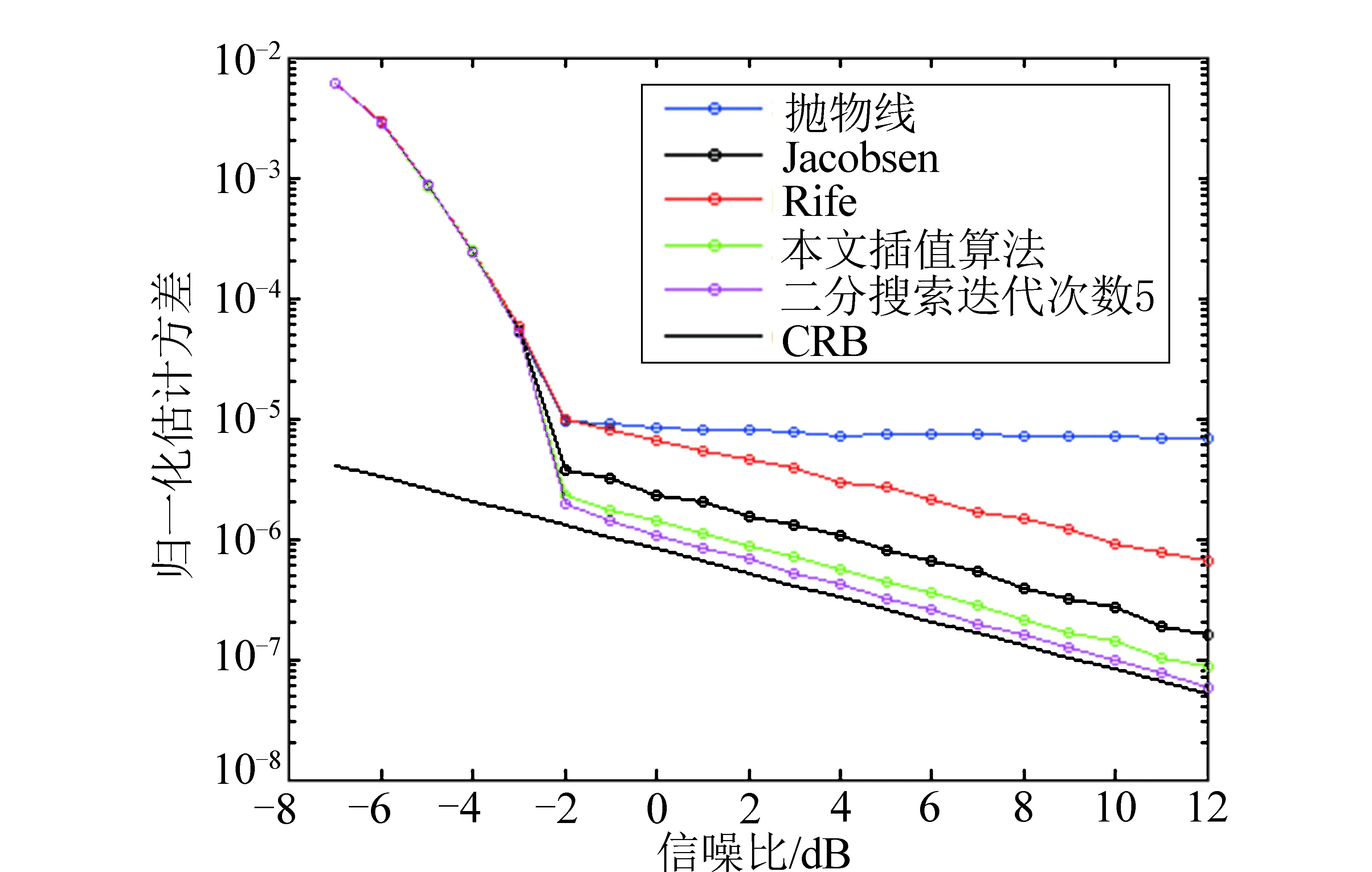
图5 算法估计精度与CRB比较(N=64)Fig.5 Comparison of estimation accuracy with CRB (N=64)

由以上分析可知，在探测器应答机设计中，采用本文算法，需要考虑的两个主要参数为：①二分搜索迭代次数；②估计序列长度。由于探测器硬件资源有限，二分搜索迭代次数一般不超过5。估计序列长度为64、128、256时，对应的载波同步门限分别为-2 dB，-5 dB、-8 dB；估计序列越长，信道利用率越低，实现复杂度也会相应增加。在应用时可根据系统对载波同步门限的具体指标要求选择适当的估计序列长度。

5 工程应用

目前，该算法已应用在深空探测器应答机的遥控解调软件设计中。与载波同步相关的技术指标包括：中频频率范围为45～55 MHz，频偏范围为±100 kHz，载波同步门限为2 dB，帧头长度为64。软件采用图1所示的解调结构，其中频偏估计部分采用本文提出的基于插值的FFT频偏粗估计和基于二分搜索的频偏精估计结合的算法。硬件平台选用Xilinx Virtex-4系列现场可编程门阵列(Field Programmable Gate Array, FPGA)，具体实现步骤如下：

(1)中频信号经过ADC采样后转换为8 bit数字中频信号。

(2)对数字中频信号进行下变频和匹配滤波。

(3)匹配滤波后的数据送至位同步模块，恢复最佳采样点信息。

(4)最佳采样点信息序列首先通过已知帧头去掉调制信息，获得长度为64的估计序列，接下来采用本文提出的算法获得频偏的估计值。初始的FFT计算选用FPGA内自带的Fast Fourier Transform IP核实现，精估计阶段的二分搜索迭代次数选择5。

(5)用频偏估计值对最佳采样点信息序列进行相位补偿，补偿后的序列可直接进行MPSK解调和译码。

根据仿真分析可知，帧头长度为64时，本文算法的载波同步门限为-2 dB，在FPGA开发过程中数字化处理引入2 dB的损失，仍留有约2 dB的余量，满足技术指标要求。相比于传统深空探测器应答机中采用的锁相环算法，性能优化大于4 dB。在探测器工程应用中，硬件开销是算法需要考虑的一个关键问题，实现该算法的资源消耗情况见表1。由表1可知，相较于锁相环算法，本文算法资源开销稍大。但随着航天器芯片技术的发展，逻辑资源丰富、可灵活配置的静态随机存储器(Static Random Access Memory, SRAM)型FPGA在航天器设计中的应用越来越广泛，资源消耗已不是制约算法选择的瓶颈。

表1 算法实现资源开销

6 结束语

根据深空通信信噪比低，动态范围大的特点，本文设计了一种基于插值的FFT频偏粗估计和基于二分搜索的频偏精估计结合的载波同步算法。目前，该算法已应用于深空探测器的遥控数字解调软件设计中。工程实践表明，采用该算法实现的数字解调器能够实现信噪比2 dB条件下的载波恢复，相比于传统的锁相环载波同步算法，性能提升不小于4 dB。