基于TexGen的筒状纬编针织物的三维仿真

朱生群 袁嫣红 李跃珍

摘 要：为建立筒状纬编针织物三维几何模型，突出其立体感，以传统的二维Pierce线圈模型作为织物在其厚度方向上的投影，利用几何关系得到能描述纬编针织物纱线形态的15个节点及其二维坐标值的计算方法，再将织物厚度方向扩展为节点坐标的第三维度，根据节点位置的不同得到其三维坐标值，基于这些节点在TexGen软件中使用Bezier樣条曲线建立织物的纱线轨迹，再以指定的纱线横截面形状扫掠轨迹，建立通用的筒状纬编针织物三维模型。模拟结果较好地表现了线圈的相互串套关系和织物的空间形态，且能为后续的有限元分析提供前处理工作。

关键词：TexGen;Pierce线圈模型;筒状纬编针织物;几何建模;三维仿真

中图分类号：TS186.2

文献标志码：A

文章编号：1009-265X（2019）06-0057-05

Abstract：A three-dimensional geometric model of tubular weft-knitted fabric has been established to highlight its dimensional effect. The traditional two-dimensional Pierces loop model was used as the projection of the fabric in its thickness direction. 15 nodes describing the yarn shape of weft-knitted fabric and the calculation method of their two-dimensional coordinates were obtained based on the geometric relationship. The thickness direction of fabric is extended as the third dimension of every node， and the three-dimensional coordinate values of node was obtained according to the different positions of the nodes. The yarn trajectory of the fabric was established with Bezier spline curve in TexGen software based on these nodes， and then the general three-dimensional model of tubular weft knitted fabric is established by sweeping the trajectory with the specified yarn cross-section shape. The simulation results reflect the interlacing of coils and spatial form of fabrics well， and can provide pretreatment for the subsequent finite element analysis.

Key words：TexGen; Pierces loop model; tubular weft-knitted fabric; geometric modelling; 3D simulation

随着计算机图形学技术的进步，各类织物的结构研究及三维模拟都有了长足的发展，纬编针织物作为针织物的一大分类，在现实生活中应用十分广泛，其结构复杂，形态多变。对其结构的研究，目前正在从二维模拟转换到三维模拟。丛洪莲等[1]使用NURBS曲线的方法建立了经编针织物的三维结构模型，王辉等[2]利用B样条曲线建立了织物纱线的结构模型，吴周镜等[3]利用OpenGL和VC++模拟了实际织物的光照效果。但是对于袖筒、裤管、袜筒等筒状纬编针织物，现在还缺乏对其结构的深入探究。本文改进了Pierce线圈模型，基于TexGen软件对筒状纬编针织物进行三维仿真，分析了其结构特点，模拟了其在空间中的三维几何结构，有助于将理论研究与设计生产密切结合起来，可以预测编织效果，减少试织和实验过程，节约生产成本，为产品设计和生产提供理论基础。

1 纬编针织物线圈结构的建模方法

对纬编针织物的模拟研究始于20世纪20年代，逐步从二维平面线圈建模过渡到三维空间线圈建模及织物形态和质感的模拟，目前国内外对纬编针织物的模拟主要为Pierce模型法、分段函数法和样条曲线法。

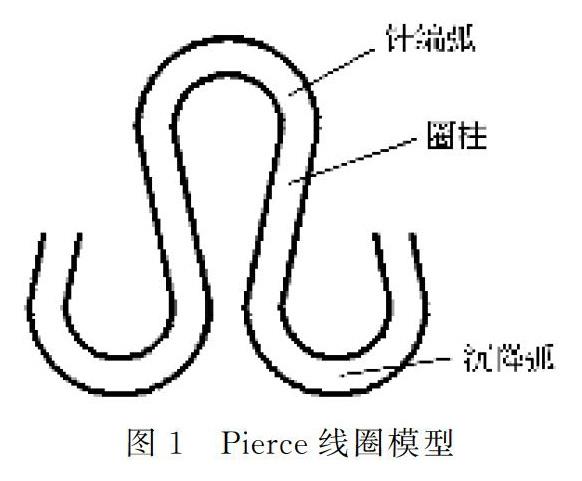
Pierce线圈模型在目前的研究中使用十分广泛，其是一种简单的二维线圈模型，以实际观察的大量纬编针织物线圈形态为基础，将线圈单元的针编弧和沉降弧假定为圆弧，圈柱假定为直线段连接针编弧和沉降弧，以此完成模型的建立[4]，如图1所示。然而这种建模方法仅能反映织物纱线在二维平面内的轨迹，并未考虑织物厚度，不能描述织物在空间中的的真实形态。为了表示织物线圈的空间形态，分段函数法根据线圈结构将其分成不同的段，每段由相应的函数来描述纱线的空间走向，以此建立织物的空间模型[5]。其实现了织物模型的空间立体感，但确定分段函数比较困难，计算复杂。样条曲线法是由Bezier曲线或非均匀有理B样条（NURBS）曲线等来描述纱线中心轴线的空间轨迹，其使用灵活稳定，目前广泛应用于线圈的三维模拟中[6]。

2 TexGen软件对筒状纬编针织物的建模方法

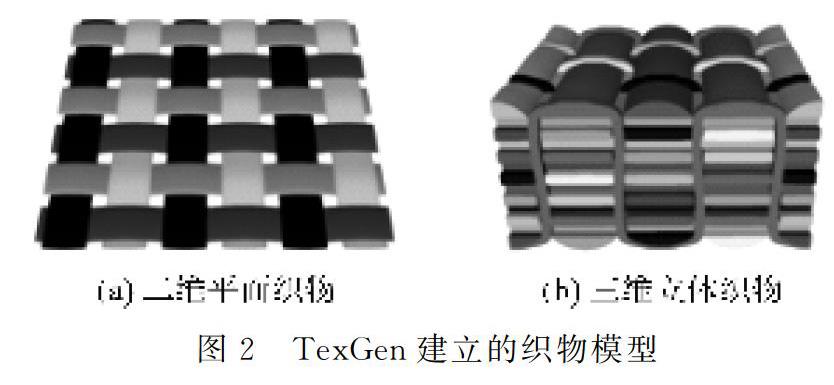
TexGen是由英国诺丁汉大学基于GNU GPL许可证开发的开放源代码软件，主要用于各类织物结构的几何仿真，其对机织物、经编和纬编织物都能提供良好的结构仿真效果，如图2所示，还能作为纺织力学、渗透性等性能分析模型的基础[7]。

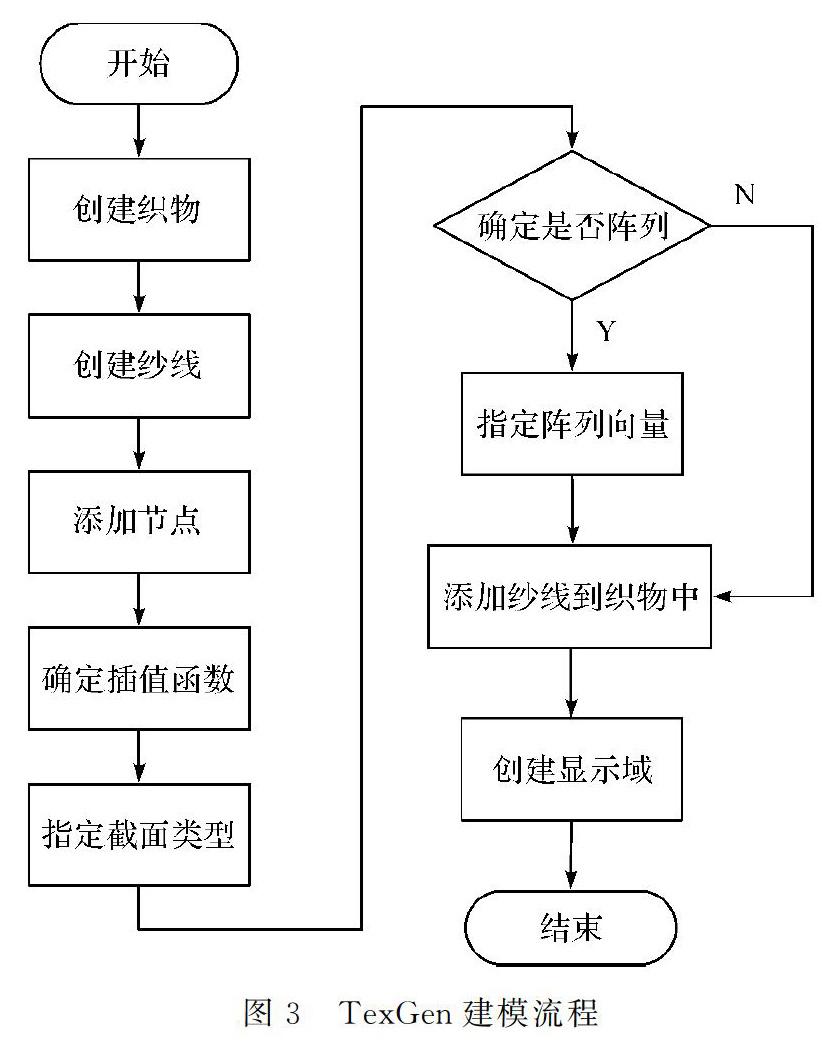
TexGen可以使用软件本身的GUI界面或编写Python脚本来建立织物模型，建模方法是先指定一系列织物纱线轨迹上的节点，通过Bezier曲线或3次自然周期插值曲线等样条曲线建立纱线的中心轴线，再以创建的横截面扫掠中心轴线来生成线圈单元模型，在空间中的3个方向上均可以对线圈单元进行阵列，以此获得织物的整体三维模型。其中横截面可指定为圆形、椭圆、动力椭圆等多种类型，且横截面可在指定的节点或位置上创建不同的类型以贴近纱线的实际形态[8]，建模过程如图3所示。

由于Pierce线圈模型是理想化的二维线圈模型，缺少在织物厚度方向上的维度，仅能示意线圈中纱线的平面轨迹，不能表达织物的三维立体感，且无法通过模型获得织物组织符合实际的线圈长度，故本文在此线圈模型的基础上，将织物的厚度方向作为第三维度加入进去，在TexGen中使用Bezier样条曲线来建立袜筒、裤管等圆筒形状的纬编针织物，其模型立体感强，且可调用内置的length函数直接得到线圈单元中的纱线长度。

通常织物的厚度大于等于所用纱线直径的2倍，TexGen中为参数化建模，可以将织物厚度与纱线直径的比值作为建模时的一个输入参数，本文后续的建模均假设织物的厚度为纱线直径的2倍。根据其建模原理，先建立能描述纱线形态的平铺状最小线圈单元模型，再将平铺线圈单元包覆在柱状腿部模型上得到曲面型的線圈单元，最后通过圆周阵列和水平阵列的方法得到圆筒径向和轴向上的纱线模型，以此建立筒状纬编织物。

3 平铺状线圈单元模型的建立

令三维线圈单元在沿着厚度方向上的平面投影为Pierce线圈，据此在TexGen中建立平铺状最小线圈单元模型。根据TexGen的建模流程，首先需要确定建立纱线中心轴线所需的一系列插值节点，基于Pierce线圈模型，在线圈的纱线中轴线上选择如图4所示的n1～n15共15点作为插值节点，沿着纱线方向从左上到右上将节点从n1开始依次编号，其中n1、n3、n6、n8、n10、n13、n15这7点描述了线圈单元的极限位置，n2、n4、n5、n7、n9、n11、n12、n14这8点描述了纱线相互交叠的关键位置，则这15个节点可以比较准确的反映线圈形态和相互串套关系。

令织物圈距为A，圈高为B，圈弧所在圆的半径为r，纱线半径为r0，建立如图5所示的空间直角坐标系1，其中Z轴表示织物的厚度方向，线圈单元关于OYZ平面对称，设节点ni的坐标为（xi，yi，zi），则i的取值范围为正整数1～15。

对于描述线圈单元极限位置的节点，由几何位置和对称关系，易知节点的坐标值为：

对于描述线圈单元关键位置的节点，可先求出n2和n4节点坐标值，其余节点可通过平移和对称关系得到。

对于节点n2，其Z轴坐标由纱线交叠关系可知z2=3×r0，n2在OXY面上的投影为圈柱所在直线与针编弧所在圆的交点，该交点的坐标值可由式（1）方程组求出：

由式（1）可解得两组交点坐标值，舍去无效交点，得到节点n2的X轴与Y轴坐标值：

对于节点n4，与节点n2类似，其Z轴坐标z4=r0，X轴与Y轴坐标可由以下方程组求出：

由平移和对称关系可知其他节点坐标为：

确定所有插值节点的坐标值后，在Pthon脚本中先通过类CTextile创建织物，再通过类CYarn为织物添加纱线，接着依次调用类方法AddNode将所有插值节点的坐标值传入，AssignInterpolation指定样条曲线所用的插值函数，本文中指定为Bezier样条曲线，AssignSection指定纱线横截面形状，即可建立平铺状线圈单元模型，如图6所示。

4 筒状针织物模型的建立

人体各部位的曲率半径一般是不同的，对于筒状织物来说，其穿着部位一般为腿部、臂部等柱状形体，为降低建模难度，可设定一模拟穿着部位的基圆柱体，以穿着部位的平均周向长度作为该圆柱体的底面圆形周长，织物套在基圆柱体上模拟实际的穿着状态。建模的思路是将上述建立的平铺最小线圈单元包覆到此基圆柱体上，计算上述节点变换之后的标值，建立筒状针织物的最小线圈单元模型，最后对最小线圈单元进行圆周和纵向阵列，以此得到完整的纱线模型。

设织造筒状织物的圆纬机的织针数目为C，则基圆柱体的半径R可由式（3）计算：

以基圆柱的底面圆心为坐标原点，OXY面与底面重合，Z轴与中轴线重合，建立空间直角坐标系2，则在坐标系1下的每一对关于OYZ面对称的节点之间的连线线段，变为在坐标系2下包覆在基圆柱体上的弧长，此线段与弧长的长度应该相等。据此原理可知该弧的弧度为：

式中：rad为两对称点之间的连线在坐标系2下包覆基圆柱体的弧度。

设节点nj在坐标系2下的坐标值为（xj，yj，zj），j的取值范围为正整数1～15。令坐标系2中包覆在基圆柱上的最小线圈单元关于OXZ平面对称，则可求得nj的坐标值为：

对位于OXZ平面下侧的n1～n7这7个节点，上式中rad前取负号，对位于OXZ平面上侧的n9～n15这7个节点，式（5）中rad前取正号，节点n8在OXZ平面上，rad的值为0，取正负号均可。

由式（5）即可得到筒状针织物的最小线圈单元节点值坐标，对其做圆周阵列可得到基圆柱圆周方向上完整的一圈织物线圈单元模型，最小线圈单元在基圆柱圆周上所占的弧度θ为：

按照θ进行圆周阵列后的节点坐标设为（xk，yk，zk），则

式中：t为值小于C的正整数。

t是最小线圈单元在圆周方向上的阵列次数，t为1时即为上述关于OXZ平面对称的线圈单元。图7为按圆周阵列后的线圈模型。

再对圆周阵列后的织物线圈单元模型在z轴方向上阵列，在TexGen中使用类方法AddRepeat进行阵列，得到完整的筒状针织物三维模型，如图8所示，该模型较为贴近实际的织物形态，且符合纬编针织物线圈之间的串套关系。

5 結 语

本文改进了经典的Pierce纬编针织物线圈模型，加入了织物的厚度方向作为新的维度，弥补了其无法表现织物三维空间形态的缺点。文中确定了能描述最小线圈单元形态的15个插值节点和节点坐标值计算方法，采用参数化建模方法，基于TexGen软件建立了通用的筒状纬编针织物三维模型。TexGen还有与有限元仿真软件Abaqus的接口，其可以对建立好的模型进行网格划分、边界条件设定等有限元分析的前处理动作[9]，对织物模型的下一步分析提供良好的支持。

参考文献：

[1] 丛洪莲，葛明桥，蒋高明.基于NURBS曲面的经编针织物三维模型[J].纺织学报，2008，29（11）：132-136.

[2] 王辉，方园，潘优华.纬编针织物线圈模型的分析与研究[J].浙江理工大学学报，2008，25（5）：521-525.

[3] 吴周镜，宋晖，李柏岩，等.纬编针织物在计算机中的三维仿真[J].东华大学学报（自然科学版），2011，37（2）：210-214.

[4] PEIRCE F T. Geometrical principles applicable to the design of functional fabrics[J]. General Information， 1947，17（3）：123-147.

[5] VASSILIADIS S G. Geometrical modelling of plain weft knitted fabrics[J]. Indian Journal of Fibre and Textile Research， 2006，32（3）：62-71.

[6] PIEGL L. Modifying the shape of rational B-splines： part 2： surfaces[J]. Computer Aided Design， 1989，21（9）：538-546.

[7] 徐海燕，蒋金华，陈南梁.基于TexGen的经编针织物的三维仿真[J].纺织学报，2015，36（3）：140-146.

[8] LIN H， LONG A C， SHERBURN M， CLIFFORD M J. Modelling of mechanical behaviour for woven fabrics under combined loading[J].International Journal of Material Forming， 2008，1（1）：899-902.

[9] LIN H， BROWNL P， LONG A C. Modelling and simulating textile structures using TexGen[J]. Advanced Materials Research， 2011，331：44-47.