Entropy of Vaidya Black Hole on Event Horizon with Generalized Uncertainty Principle Revisited∗

Hao Tang(唐浩), Bin Wu(吴滨), Rui-Hong Yue(岳瑞宏),and Cheng-Yi Sun(孙成一)

1School of Science,Xijing University,Xi’an 710123,China

2Institute of Modern Physics,Northwest University,Xi’an 710069,China

3Shaanxi Key Laboratory for Theoretical Physics Frontiers,Northwest University,Xi’an 710069,China

4School of Physics,Northwest University,Xi’an 710069,China

5College of Physical and Technology,Yangzhou University,Yangzhou 225009,China

Abstract In this note,we recalculate the entropy of the Vaidya black hole on the event horizon by considering the generalized uncertainty principle based on the brick-wall model.The result shows that we need not impose a cut-of fby hand anymore and the result satisfies the Bekenstein-Hawking law as well.

Key words:entropy,black hole,generalized uncertainty principle,brick-wall model,minimal length

1 Introduction

Since Bekenstein[1]and Hawking[2]proposed that a black hole should have entropy,many works are studied on the entropies of different black holes.They proved that the entropy of a black hole is proportional to its area of the corresponding horizon,which is S=A/4,where S is the entropy,A is the area of the horizon.However,the origin of the entropy is still disputed till now.Thus,many different methods have been developed to explain and calculate the entropy.[3−5]’t Hooft suggested a widely-used “brickwall”method by supposing that the quantum gases in a“wall” outside the horizon contribute the entropy,and calculating the free energy and the entropy with the Heisenberg uncertainty principle(HUP),[6]which is called the“brick-wall” method.This is a very useful and clear way to explain the origin of the black hole entropy,and the calculation is much easier than Hawking’s.In this method,It is believed that there exist a “spatial shell”,which covers the horizon of the black hole.The entropy of quantum gases which exist in the region stands for the black hole entropy.Vividly saying,this shell is just like a “wall”,which divides the space into two parts.However,the result of the calculation is always a little different with Bekenstein-Hawking law.For a Schwarzschild black hole,the result of entropy is like S=(A/4){a/[90βℓpb(b+a)]}.Only let a/[90βℓpb(b+a)]=1,the result is just the Bekenstein-Hawking entropy.

In order to satisfy the Bekenstein-Hawking law,one has to choose this“cut-of f” manually,[6]which is very unnatural.What is more,the same things also happen in different black holes.[6−15]

Recently,some works take the generalized uncertainty principle(GUP)to replace the HUP in the brick-wall method to recalculate the free energy and the entropy,and shows that the cut of fis naturally given by the minimum length indicated by GUP,which means that the unnatural cut-offs are removed and the entropies can be calculated clearly.[16−26]For instance,the Schwarzschild black hole is discussed in Ref.[16].And in Ref.[10],the authors discussed the Reissner-Nordstrm black hole.All of those articles got the entropies based on brick wall model,which replaced the HUP by GUP,and removed the unnatural cut-offs.Broadly speaking,the bound of the entropy has been obtained in this framework.

However,all those works are studied on the static spherically symmetric black holes.So it is natural to investigate the non-static black holes.In this paper,we would like to use the GUP based on brick-wall method to recalculate the entropy of a non-static spherically symmetric Vaidya black hole to check this method.

Vaidya spacetime is a solution of Einstein’s equation,which describes a spacetime with dynamical mass.The metric of the Vaidya spacetime on advanced Eddington coordinates reads[27−28]

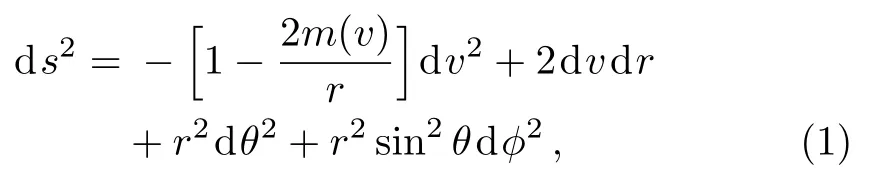
where m(v)is the dynamical mass of the black hole,v is the advanced Eddington time coordinate. We take=c=G=kB=1 in our calculation.This metric has the apparent horizon and event horizon. We have discussed the apparent horizon in Ref.[29],This time we will consider the entropy of Vaidya black hole on the event horizon.We choose following coordinate transformation[27−28]

where rEHis the event horizon and˙rEH=drEH/dv.Then,Eq.(1)becomes

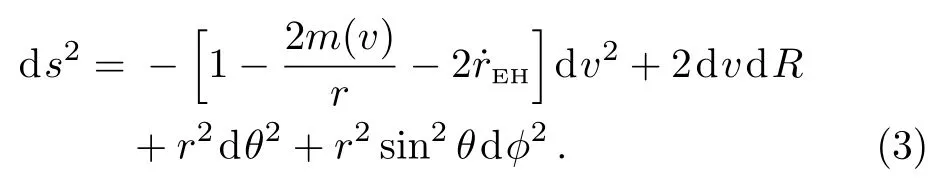
Now we let

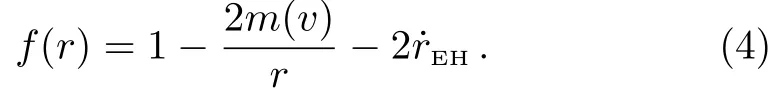
From f(r)=0,one could get the event horizon as[27−28]

The corresponding surface gravity and Hawking temperature are[27]

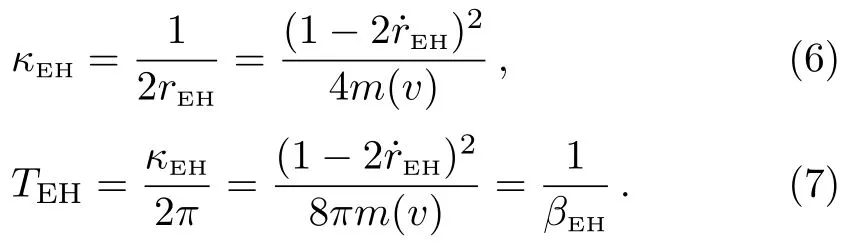
Then we have

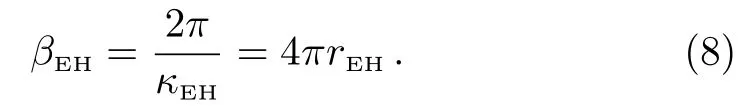
Expanding f(r)at rEH,one could get

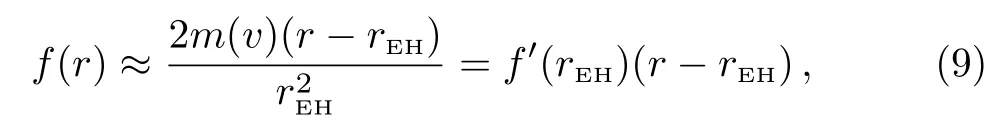
where f′(rEH)=2κEH(1−2˙rEH).

There are many ways to generalize the uncertainty principle. To demonstrate,we just take the simplest GUP[16−19,22]

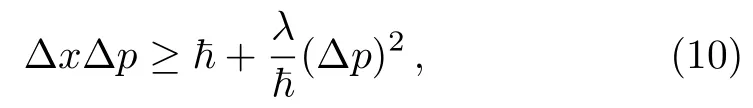
The Klein-Gordon equation for a scalar field is

Set the wave function as

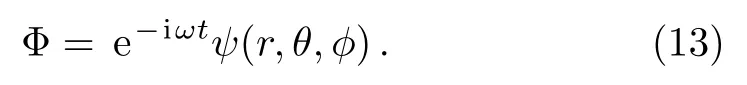
By substituting the above equation into Eq.(12),one could get

Then,take ψ ∼ eiU(r,θ,ϕ)by using the Wenzel-Kramers-Brillouin(WKB)approximation,one could get[30]

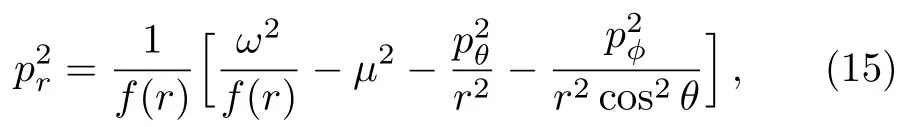
where

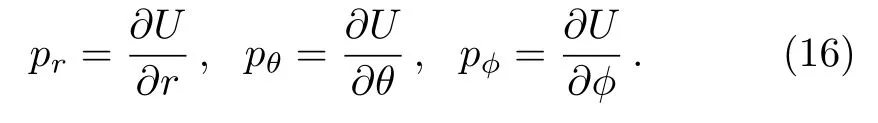
And the square module momentum is[30]

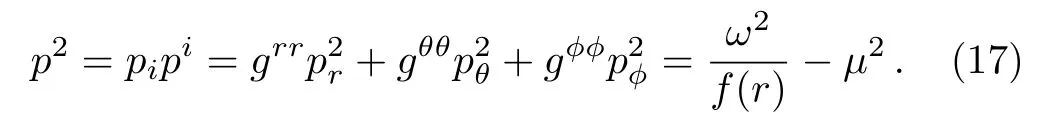
According to the statistic physics based on GUP,the quantum number now becomes[20]

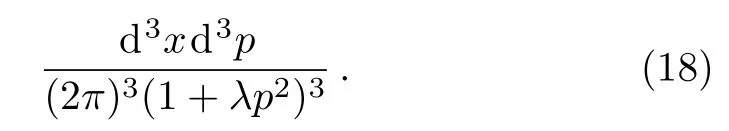
Then we obtain the number of quantum states as

One could see that we need not impose a cut-o ffby hand since the result becomes finite even at the horizon now.By using the brick-wall method,the free energy for a scalar field now reads[30]

Then the entropy is[30]

where x ≡ βEHω/2 and

It is supposed that the main contribution of entropy comes from a small region just near the horizon,[31]which corresponds to a proper distance of order of the minimal length,[30]Now we just consider a thin layer stands for the“brick-wall”,which is between rEHand rEH+ ϵEH.Then the range of integration in Eq.(19)should be changed.This method can also be used in Ref.[32]and named the thin film model,which is also improved from the brickwall model with GUP concerned.The x0goes to zero at the horizon and the entropy becomes

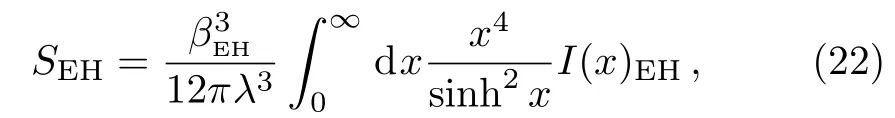
where

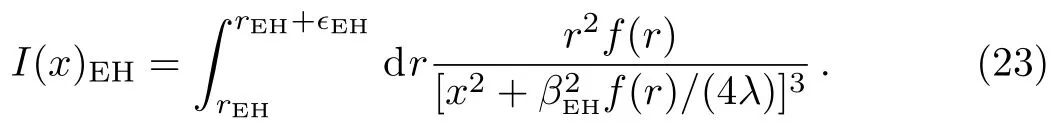
The minimal length now becomes

then one could get

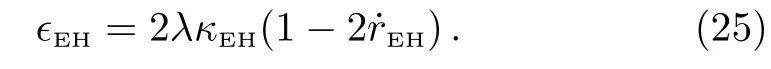
Equation(23)now can be written as

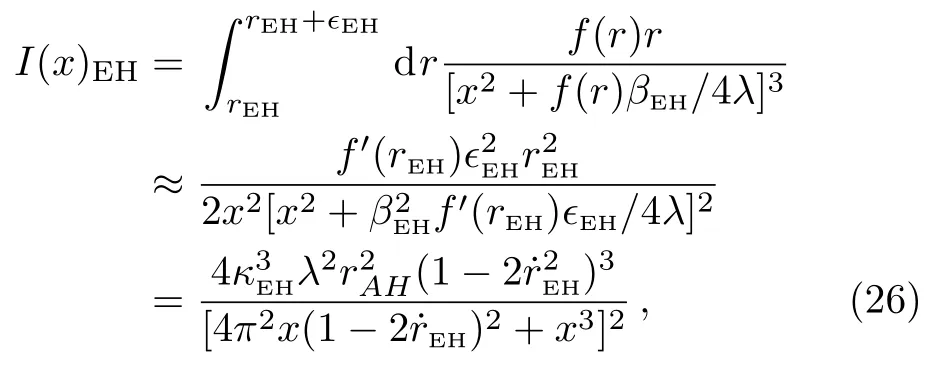
where x= βEHω/2.Then the entropy is

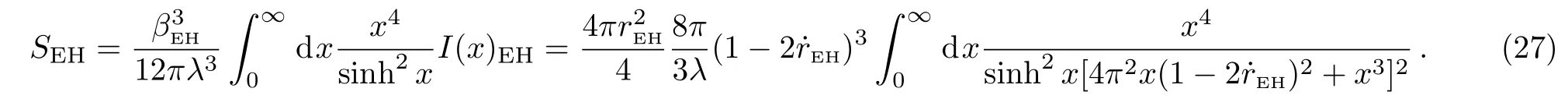
The integrand in Eq.(27)could be regarded as a complex functionusing the residue theorem,Eq.(27)now becomes

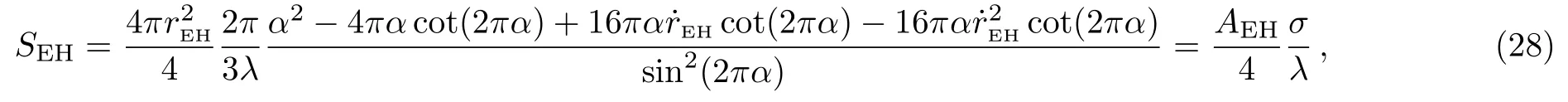
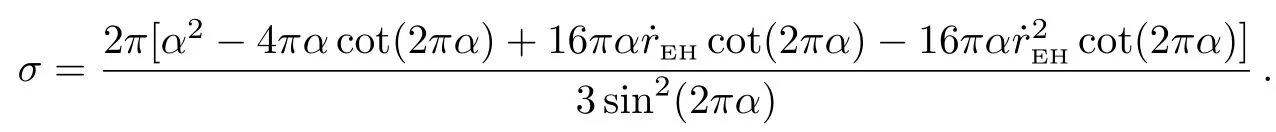
One could see that the entropy is proportional to its surface area at the horizon,and the result also satisfies some other similar works such as Ref.[27].

The method we used in Eq.(23)is similar with Ref.[32].The integration of the wall is from rEH∼rEH+ϵEH,which is a thin layer rather than a “wall”.And get the Bekenstein-Hawking naturally without cut-of f.Moreover,since the entropy is a physical property of Hawking radiation from the horizon within a Planck order thin layer,the range of integration in our method is more physical than brick-wall model.

In summary,we calculate the entropy of a Vaidya black hole on the event horizon with brick-wall method based on generalized uncertainty principle.And we find that the entropy is proportional to the surface area at the horizon,which has the same result with Bekenstein and Hawking.The result is more reliable because there is no unnatural cut-of fin this method.

Acknowledgments

We thank Mr.Bo Liu for useful comments and enlightening discussions.