Impact of Colored Noise on Population Model with Allee Effect∗
2019-01-10YaChaoYang杨雅超andDongXiLi李东喜
Ya-Chao Yang(杨雅超)and Dong-Xi Li(李东喜)
1College of Mathematics,Taiyuan University of Technology,Taiyuan 030024,China
2College of Data Science,Taiyuan University of Technology,Taiyuan 030024,China
Abstract We study a population model with strong and weak Allee effect driven by internal noise and external noise.Firstly,a single-species population model with Allee effect under environmental colored noise is established,then stable and unstable states are analyzed and interpreted in biology.After that,stationary probability distribution(SPD)of population is derived based on Fokker-Planck equation.Next,mean first-passage time(MFPT)is defined in order to quantify the transition between extinction state and survival state with Allee effect.It is found that population will not extinct when weak Allee effect exists.It is not beneficial to survival of the population with the increase of Allee threshold no matter whether strong Allee effect or weak Allee effect.When strong Allee effect occurs,the correlation time of multiplicative noise plays a positive role in survival of population,while the correlation time of additive noise has a negative effect.Crucially,the phenomenon of resonant activation is firstly discovered in population dynamics with Allee effect.The conclusions we obtain can be applied to the further research of population dynamics in ecology.
Key words:Allee effect,population model,colored noise,stationary probability distribution,mean firstpassage time
1 Introduction
The impact of noise on population model has been widely studied over several decades due to its crucial theoretical and experimental significance.The analysis usually based on bistable model driven by multiplicative noise and additive noise.The selection of noise is directly related to the accuracy of research.Accordingly,the choice of noise seems particularly critical for the study.Normally,Gaussian white noise is chosen as the stochastic perturbation of model.However,it is more reasonable to use colored noise as stochastic disturbances in the study.
Much effort devoted to the impacts of colored noise on the biological model.The influence of environmental colored noise on the single-species population system was investigated by Spanio.They concentrated on the phase transitions and how the existence of time-correlations noise affects these phase transitions in Ref.[1].The effects of colored noise on the tumor model were discussed by Bose,[2]Xu[3]and Fiasconaro[4]in modern medicine.In their work,the impacts of both noise intensity and stability index on tumor system were explored and then colored noise can enhance stability of system was found.Recently,the properties of delayed bistable model with cross-correlated colored noise and mean first-passage time of bistable dynamics models driven by colored noises were investigated by Jin et al.[5−6]Studies explored the properties of system and demonstrated that noise intensity and coupling strength could all affect mean first-passage time.Stationary probability distribution and mean first-passage time can well present the properties of model.[7−9]Additional,a three species ecosystem consisting of a prey,a predator and a top predator was studied by Das.[10]The barrier crossing dynamics with non-Gaussian noises was analyzed and resonant activation was observed by Goswami.[11]Closely,a stochastic model driven by colored noise was discussed by Zhang,[12]the researches of Fokker-Planck function and mean first-passage time were carried out.Thus the research of stationary probability distribution and mean first passage time is a crucial step toward studying of the population model.
Allee effect is a phenomenon that can not be ignored in population growth.Sometimes,population growth can not achieve exponential growth when initial size is really small(x≪K,K represents environmental carrying capacity).Thus,population growth rate may decrease and even population presents negative growth.This phenomenon is called latent period in ecology.Allee found that clusters help improve the viability of the population.Nevertheless,being too crowded or too sparse will have a negative impact on the population.It can be infered that each population has its own optimal density.Allee effect[13−18]has a significant influence on popula-tion growth.It is an interaction between population size,density and growth rate.[19]In brief,Allee effect is the dependence of reproduction on density at low density.When reproduction of population has strong dependence on its density,it is called strong Allee effect.It means population size reduce or even population extinct at low density.When reproduction of population has weak dependence on its density,it is called weak Allee effect.It indicates that population is still growing although the growth rate is low when density is small.
Allee e ff ect has attracted extensive attention due to its important biological signi ficance in recent years.The infl uence of Allee e ff ect on predator-prey system at discrete times was studied by Celik and Duman.[20]The change of equilibrium points move from unstable states to stable states under Allee e ff ect is explored in their study;The extinction conditions of isolated population with Allee e ff ect were discussed by Mendez et al.,[21]which provided valuable theoretical help in biology and medicine;The major conclusion what Allee e ff ect could enhance population stability was demonstrated by Scheuring[22]through numerical simulations of host microorganisms.Additional,Allee e ff ect also applied in the study of biotic invasion.The species invasion of stochastic population model with Allee effect was investigated by Ackleh et al.[23]They formulated the relationships between initial population size,migration rates,Allee threshold and the possibility of species invasion,then they explored the influence of Allee effect on species invasion.The impact of Allee effect on exotic species establishment is also concerned by Petrovskii.[24]It concluded that Allee effect could increase the system spatiotemporal complexity through the research.Recently,how the noise affects the behaviors of Truscott-Brindley system under weak Allee effect was analysed.[25]Studies investigated and discussed the phenomenon of stochastic excitement and Canard explosion.A new result of traveling wave solutions for a biological invasion model involving density dependent migration and Allee effect was reported by Sun.[26]Closely,a prey-predator model with strong Allee effect in the prey growth function was considered by Sen,[27]and they conducted a extensive study of the overall dynamics of the system and all possible global bifurcations that the system could undergo were explored.The single-species model and predator prey model with Allee effect was driven by colored noise terms are investigated by Sun.[28]
In this work,we focus on the impact of colored noise on single-species population model under strong Allee effect and weak Allee effect.The goal of our work is to study the model by discussing in detail how colored noise affects stationary probability distribution and mean first-passage time under different Allee effects(strong and weak).
The other parts of contents are summarized as follows.In Sec.2,we establish the system equation for a singlespecies population with Allee effect and then introduce stochastic disturbance for the system.In Sec.3,we obtain the expression of stationary probability distribution based on Fokker-Planck equation.In Sec.4,the expression of mean first-passage time under Allee effect is calculated.Simultaneously,we will focus on how colored noise affects stationary probability distribution and mean first-passage time.At last,we summarize the contents and draw conclusions in Sec.5.
2 The Model System
The deterministic system model is formally introduced and then random noise terms are added to the model in this section.For simplicity,the dimensionless formulations are adopted in the paper.Now,the most common model for describing the Allee e ff ect of a single species population is given
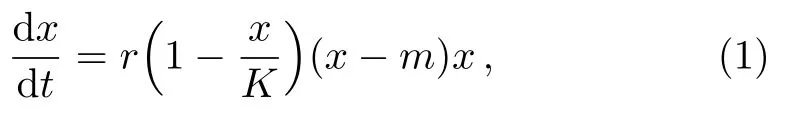
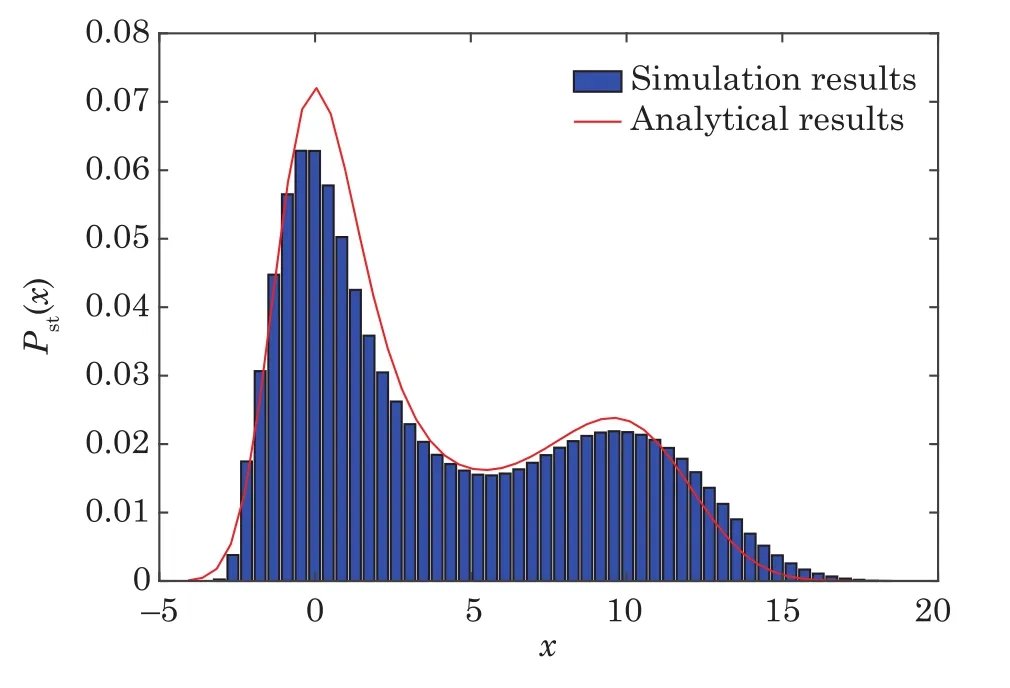
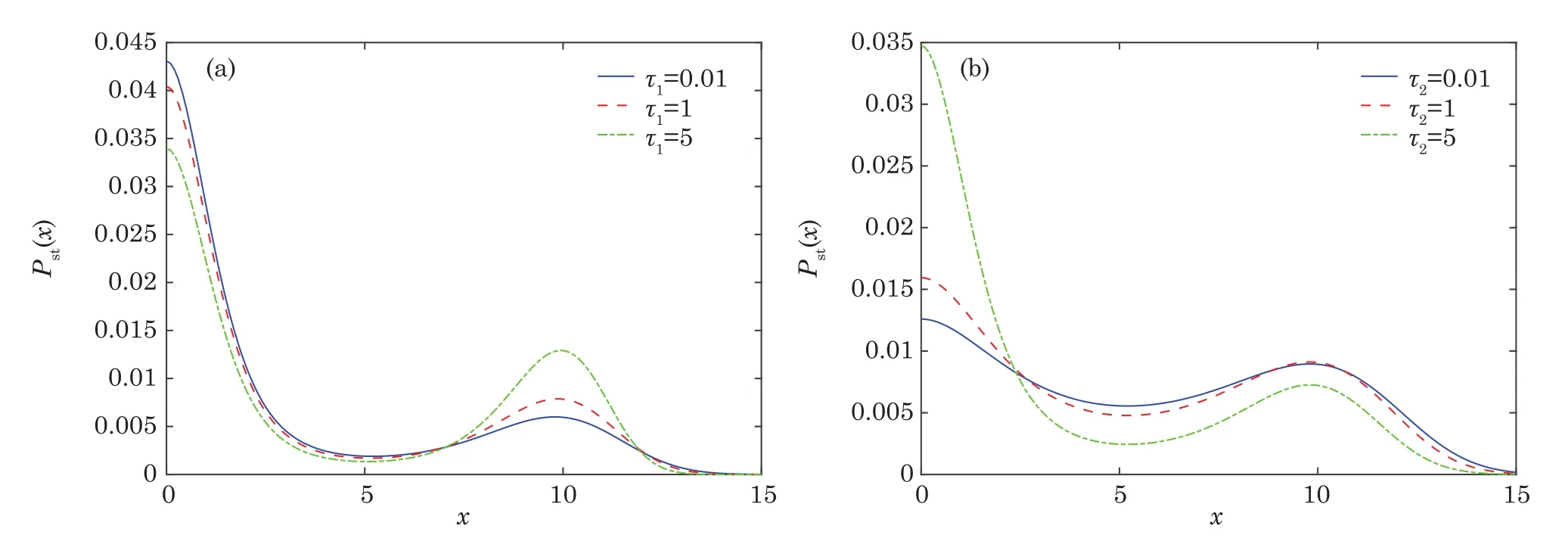
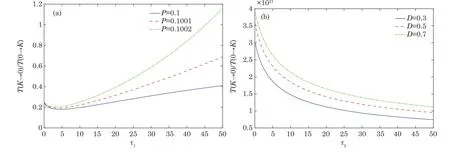
here x denotes the population size,r denotes the intrinsic growth rate in population,K denotes the environmental carrying capacity,m denotes the minimum of viable population.The need to pay attention to is that all the parameters are positive,and for biological reasons m which has two stable states xs1=0,xs2=K and an unstable state xu=m when 0 In contrast when m≤0,two stable states of the potential become xs1=m,xs2=K and unstable state becomes xu=0 in Fig.1(b).It can be inferred that the population will increase to a constant size eventually.Hence,it explains that the population will stay in a stable state of survival under weak Allee effect. The potential functions when Allee threshold m takes different values in strong or weak Allee effect are plotted in Figs.1(c)and 1(d).In Fig.1(c),the larger value of m will make the potential well at x=0 more deeper.Likewise in Fig.1(d),the potential well at x=K becomes shallower with the increase of m.Here,the potential well of x=K becomes deeper means that the possibility of survival in population increases and the state of population is more stable.Therefore,we can infer that whether it is strong Allee effect or weak Allee effect,smaller Allee threshold is better for the survival of population.Furthermore,population will maintain a steady state of survival under weak Allee effect. Fig.1 The potential U(x)as a function of x(a)strong:r=0.1,m=5,K=10;(b)weak:r=0.1,m=−5,K=10;r=0.1,K=10 is fixed in(c)and(d),m takes 1,5,9 and−1,−5,−9 respectively. The population system is disturbed by external environment.The weather conditions,temperature,amount of food,number of natural enemies and growth rate will affect the population system.A slight change may even cause major changes in the population system.Therefore,we use noise to represent stochastic perturbations that the population may suffer. Next,the random perturbations are introduced to the model.In the system,multiplicative noise is identified as internal perturbations,whereas additive noise is equivalent to external perturbations.External perturbations are supposed to originated from the environment.In contrast,internal perturbations are thought to be generated within the system.For instance,the stochastic perturbations of population size and intrinsic growth rate are regarded as internal noise.Now consider a population model driven by multiplicative noise and additive noise,which follows the Langevin equation: where ξ(t)and η(t)represent the uncorrelated Gaussian colored noises with zero-mean,whose statistical properties are given by here the parameters of P and D denote the intensities of multiplicative noise and additive noise, τ1and τ2denote the self-correlation time of ξ(t),η(t),respectively.When the limit τ1→ 0 and τ2→ 0,the system function de-generates to the model stimulated by two Gaussian white noises.[33] To investigate the influence of noise on stationary probability distribution,the expression for stationary probability distribution is calculated based on Fokker-Planck equation(FPE).According to the Novikov theorem[34]and Fox’s approach,approximate Fokker-Planck equation can be written:[33] where Here,it should be noted that approximate Fokker-Planck equation is valid under the condition 1− τir(m −K)>0,where i=1,2.Fortunately,this condition is satisfied no matter whether 0 It can also be represented as the following form: here,N represents the normalization constant andeU(x)represents the modified potential After calculation,it is obtained where c1=1−τ1r(m−K), c2=1−τ2r(m−K). Firstly,for the purpose of check the validity of approximation method used in the derivation,we use Milstein method to take numerical simulation of SPD.The analytical results and simulation results of SPD are shown in Fig.2.From the figure,we can see that the analytical results is agree with the simulation results.Next,we mainly consider the impact of noise and Allee effect on the SPD. Fig.2 Numerical simulation of the SPD Pst(x)when 0 Fig.3 The SPD Pst(x)as a function of x when 0 Fig.4 The SPD Pst(x)as a function of x when m ≤ 0;(a)r=0.1,m= −5,K=10,D=0.2,τ1=0.2,τ2=0.5 are fixed,P takes 0.01,0.1,1,and 2;(b)r=0.1,m= −5,K=10,P=0.5,τ1=1,τ2=1 are fixed,D takes 0.01,0.1,1,and 2. Fig.5 The SPD Pst(x)as a function of x when 0 Fig.6 The SPD Pst(x)as a function of x when m ≤ 0;(a)r=0.1,m= −1,K=10,P=0.6,D=0.5,τ2=0.5 are fixed,τ1varies from 0.5,5 to 50;(b)r=0.1,m= −1,K=10,P=0.3,D=0.5,τ1=0.2 are fixed,τ2varies from 0.5,5 to 50. We consider the effects of noises intensities on the SPD under strong Allee effect in Figs.3.The curves in Fig.3(a)present a unimodal structure at x=0.The peak decreases in height when the intensity of multiplicative noise P increases.In Fig.3(b),the proportion of curves around x=0 decreases while the proportion around x=K increases as the intensity of additive noise D grows.From Fig.3,we can infer that the increase of intensity of the multiplicative noise is beneficial to the survival of population when the intensity of additive noise is not relatively small(as D=0.3 in Fig.3(a)).Similarly,the likelihood of extinction in population will also reduce when the intensity of additive noise increases.Nevertheless,the population will stay in an extremely unstable state when intensity of additive noise reaches a relatively large size. Figure 4 displays the SPD as a function of population size x with different noise intensities under weak Allee effect.Obviously,the graphs of SPD display a unimodal structure when m≤0.As we can observe,the position of peak experiences a transition from x=K to x=0 in Fig.4(a).Before P reaches a certain level,the peak around x=K decreases in height as P grows.After P reaches a certain level,the position of peak changes from x=K to x=0.Simultaneously,larger value of P will make the peak around x=0 become more pronounced.In contrast in Fig.4(b),SPD is weakly affected by the intensity of additive noise D.The value of D increase from 0.01 to 2,but the curve of SPD does not change signif icantly either at height of peak or position of peak.It is concluded that the increase in intensity of multiplicative noise is not advantage to the survival of population under weak Allee effect.Only when the intensity of additive noise is large,the increase in intensity of additive noise will cause a relatively pronounced change in population. Figure 5 shows the curves of SPD as a function of the population size x with different values of noise correlation time τ under strong Allee effect.In Fig.5(a),left peak of SPD becomes lower while the right peak of SPD becomes higher when τ1increases.On the contrary,the left peak of SPD becomes higher while the right peak of SPD becomes lower when τ2increases in Fig.5(b).Clearly,two curves always show bimodal structure in Fig.5.Comparing Fig.5(a)with Fig.5(b),we can know that selfcorrelation time τ1and τ2have similar but not identical effects on SPD.In biology,when strong Allee effect occurs,the increase in correlation time of multiplicative noise will increase the possibility of survival of population,while the increase in correlation time of additive noise will reduce the possibility of survival of population,even the population might be vulnerable to extinction.Furthermore,when self-correlation time is small,the population will be weak effected by the increase of self-correlation time under strong Allee effect. Figure 6 shows the influence of noise correlation time τ on SPD under weak Allee effect.Clearly,Fig.6 presents a unimodal structure around x=K.In Fig.6(a),the increase in correlation time of multiplicative noise τ1can strongly enhance the peak of SPD.While in Fig.6(b),there are little change of curves with the increase of τ2.This observation means that self-correlation time of multiplicative noise has more pronounced impact on SPD than additive noise when weak Allee effect occurs.In practice,the increase in correlation time of multiplicative noise is beneficial to the survival of population when weak Allee effect happens. Fig.7 The SPD Pst(x)as a function of x;(a)r=0.1,K=10,P=0.05,D=1,τ1=2,τ2=5 are fixed,m varies from 3,3.5,to 4;(b)r=0.1,K=10,P=0.05,D=1,τ1=2,τ2=5 are fixed,m varies from −1,−3,to−5. Figure 7 reveals the direct effect of Allee threshold m on the SPD.In Fig.7(a),curves always display a bimodal structure with the change of m.Simultaneously,the left peak of SPD grows higher while the right peak of SPD becomes lower when m increases under 0 In order to study the model in more depth,it is essential to estimate the amount of time between shifts from one stable state to another.It contributes to quantify the influence of noise on the state transitions between stable states.This time is called the first passage time.When the first passage time is averaged in many realizations,the result is called mean first-passage time.The longer mean first-passage time explains that the state is more steady.[36] In this paper,we focus on the transition of population from the state of survival to the state of extinction.Hence,the mean first-passage time from one stable state xs2=K to another xs1=0 under strong Allee effect is given by the following expression:[37−38] T can be calculated by applying the steepest-descent approximation to Eq.(9): where the U′(x)represents the second derivation with respect to x.Now the final expression of MFPT is derived by inserting Eqs.(2)and(8)into Eq.(10): Fig.8 The MFPT as a function of noise intensity when 0 Figure 8 displays the direct impact of noise intensity on MFPT.In Fig.8(a),we can observe that curves descend first and then rise with intensity of additive noise D.Nevertheless,MFPT is strongly affected by D when P is really small,but when P=0.2,MFPT is weakly affected by D.The phenomenon of resonant activation[39]will happen when D reaches a certain size.From Fig.7 we can conclude that behaviors of MFPT are sensitive to small intensity of multiplicative noise.If intensity of multiplicative noise is relatively large,the changes of additive noise intensity will have little effect on the transition between stable states.More important,the phenomenon of resonant activation will occur when additive noise intensity D reaches a certain size.So when strong Allee e ff ect occurs,the increase in intensity of additive noise will contribute to the development of population after resonant activation happens. Comparing with Fig.8(a),Fig.8(b)shows the e ff ect of noise intensity on MFPT in another form.In Fig.8(b),when D=0.01 and D=0.1,the curves of MFPT descend first then become gentle as P grows.In contrast when D=0.3 and D=1,the curves rise first and then become gentle.Clearly,curves finally converge to a stable state.This observation also reveals that MFPT is sensitive to small intensity of multiplicative noise.When intensity of multiplicative noise reaches a certain size,the changes in intensity of multiplicative noise will have weak effect on the population.Furthermore,the influence of noise intensities on the population is also restricted by other parameters.When intensity of additive noise is small,the increase in intensity of multiplicative noise will have an adverse effect on the survival and stability of population.When the intensity of additive noise is relatively large,the increase in intensity of multiplicative noise will play a positive role in population growth.Besides,these conclusions further verify the results of Fig.3(a)and Fig.8(a). Figure 9 shows curves of the ratio of MFPT in opposite directions as a function of correlation time with different noise intensities.In Fig.9(a)the ratio increases monotonously when τ1increases,while the curves decrease monotonously as τ2grows in Fig.9(b).Furthermore,even a minor change in P can cause a pronounced change in ratio as shown in Fig.9(a).When we fix the value of correlation time,the ratio becomes larger as the noise intensity increases.The plots in Fig.9 imply that behaviors of the ratio are sensitive to the intensity of multiplicative noise.It is beneficial to the survival of population with the increase in correlation time of multiplicative noise,at this time the population will be in a state of survival.On the contrary,it has a negative influence on the survival of population as correlation time of additive noise increases,even the population may extinct at this time.These results can also verify the conclusions in Fig.3,Fig.5,and Fig.8. Fig.9 The ratio of MFPT in two opposite direction as a function of noise correlation time τ;(a)r=0.01,m=5,K=10,D=0.5,τ2=0.1 are fixed,P takes 0.1,0.1001,and 0.1002;(b)r=0.01,m=5,K=10,P=0.5,τ1=0.1 are fixed,D takes 0.3,0.5,and 0.7. Fig.10 The MFPT as a function of Allee threshold m when 0 Figure 10 depicts the curves of MFPT as a function of Allee thresholds m with different values of intrinsic growth rate r at 0 We discuss the impacts of colored noise on the population model with Allee e ff ect in this paper.We firstly establish the single-species population model.Next,we explore the stationary probability distribution and mean first-passage time of system.Meantime,we also discuss in detail how colored noise a ff ects stationary probability distribution and mean first-passage time. It is found that noise intensity,correlation time,Allee threshold and intrinsic growth rate can all affect stationary probability distribution and mean first-passage time.It is noteworthy that effect of many parameters on the population is often restricted by other parameters,which restrict each other and jointly affect the survival and stability of the population.Whether it happens strong Allee effect or weak Allee effect,the smaller Allee threshold is better for the survival and stability of population.Importantly,the occurrence of weak Allee effect has positive influence on the survival of population.These conclusions play a significant role in the study of ecological problems in the future.In general,the increase in intensity and correlation time of multiplicative noise all favors the stability of population under strong Allee effect.In contrast when weak Allee effect occurs,the increase in correlation time of multiplicative noise will have benefits for the survival of population,whereas the increase in intensity of multiplicative noise may lead to the extinction of population at this time.Surprisingly,the phenomenon of resonant activation is firstly discovered in population dynamics with Allee effect.This discovery makes the research more novel and our conclusions become more abundant. Allee effect can deeply affect the integrity of population or dynamic status of the whole community.Some scholars pointed out dynamic instability like Allee effect can be used as the impetus of evolution for highly developed species in the system.Obviously,Allee effect plays a pivotal role in biological evolution and our research of Allee effect is particularly necessary. In brief,noise and Allee effect are two principle elements in ecology.In this work,phase transition is induced by noise.Besides,the phenomenon of resonant activation is caused by both noise and Allee effect.Previously,it is demonstrated that noise can enhance the stability of prototype dynamical system and resonant activation.[40]While in the population system,the phenomenon of resonant activation is the result of interaction between noise and Allee effect. Further work on analysing impact of colored noise on population is needed.In practice,colored noises are correlated,they interact with each other and affect the system together.Hence,the coupling strength of noise is another important factor affecting the model.The correlated colored noise can be considered in the population model as the next step.Additionally,internal noise can affect directly on the intrinsic growth rate,which is also one aspect of our next work can be improved.Our work is to investigate the population dynamics based on time variation.Besides,there are many researches of population dynamics based on spatial changes.The influence of time delay and spatial diffusion on herbivore system were studied by Li[41]and Sun.[42]The stability behaviors of a marine prey-predator model was considered by Gazi,[43]they studied the reaction diffusion equation and analyzed the influence of diffusion on the stability.A predator prey model with spatial motion was studied by Sun,[44]they found isolation degree of spatial patterns have a significant effect on the persistence of population.For this,our future work can be extended to the analysis of the dynamic behaviors of population system based on time variation and spatial motion.More specific investigates of Allee effect and colored noise on population are major challenges that worth extensive attention and intensive research.Still,our work is a crucial step toward resolving these challenges.


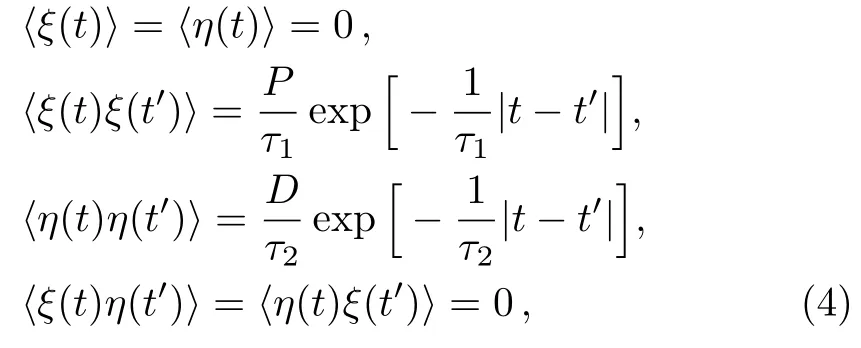
3 Stationary Probability Distribution
3.1 Derivation of the Stationary Probability Distribution
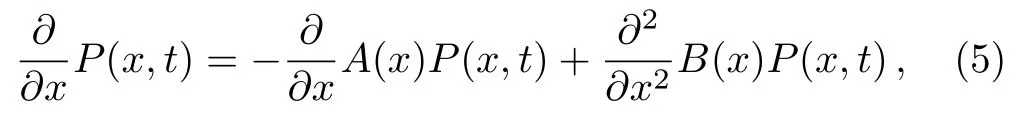
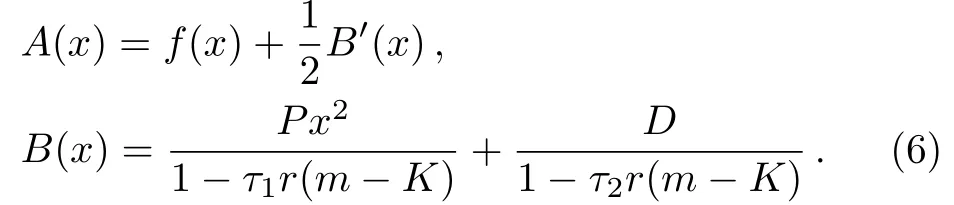
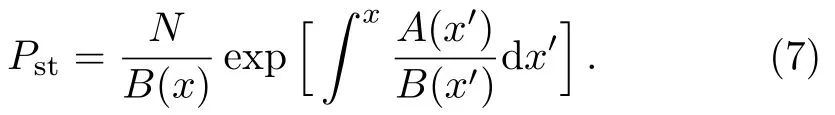
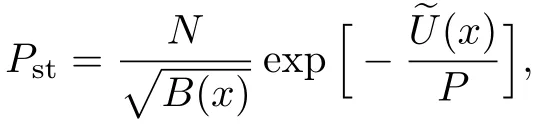
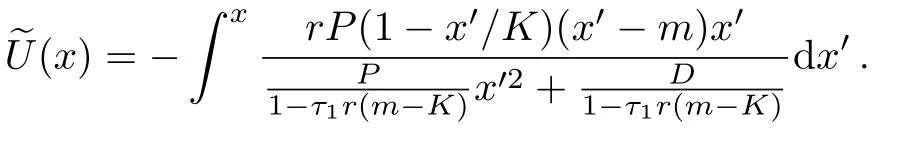

3.2 Discussion and Biological Interpretation




4 Mean First-Passage Time
4.1 Derivation of the Mean First-Passage Time

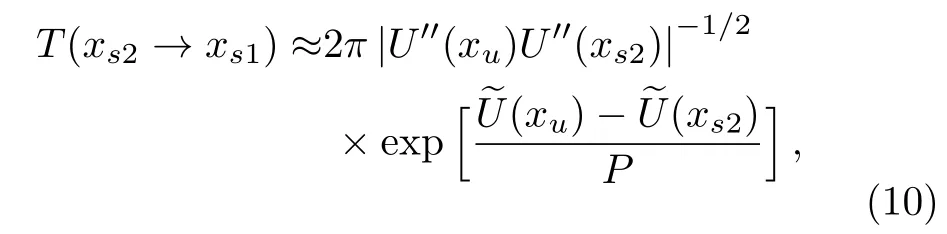
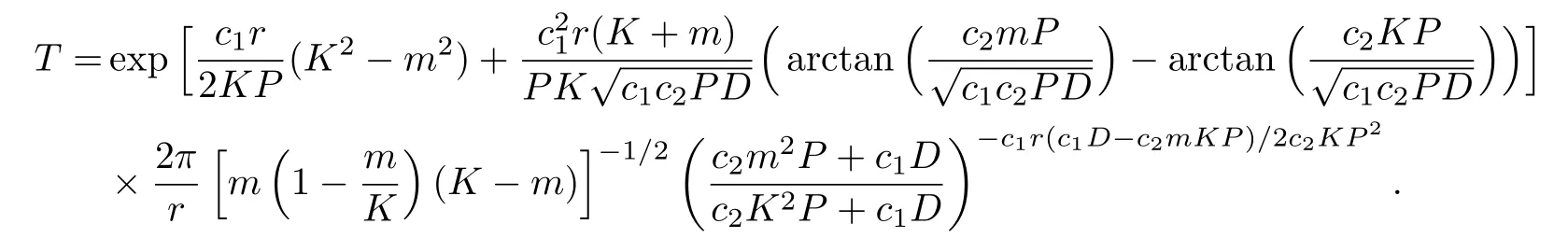
4.2 Discussion and Biological Interpretation


5 Conclusion
杂志排行
Communications in Theoretical Physics的其它文章
- Kinetic Simulation of Nonequilibrium Kelvin-Helmholtz Instability∗
- Nontrivial Effect of Time-Varying Migration on the Three Species Prey-Predator System∗
- A One-Dimensional Discrete Boltzmann Model for Detonation and an Abnormal Detonation Phenomenon∗
- Improved Five-Parameter Exponential-Type Potential Energy Model for Diatomic Molecules∗
- Dynamically Tunable and High-Contrast Graphene-Based Terahertz Electro-Optic Modulator∗
- Multipolar Structure of Equilibrium Shear Flow Field in Toroidal Plasmas∗
