A One-Dimensional Discrete Boltzmann Model for Detonation and an Abnormal Detonation Phenomenon∗
2019-01-10YuDongZhang张玉东AiGuoXu许爱国GuangCaiZhang张广财andZhiHuaChen陈志华
Yu-Dong Zhang(张玉东),Ai-Guo Xu(许爱国), Guang-Cai Zhang(张广财),and Zhi-Hua Chen(陈志华)
1Key Laboratory of Transient Physics,Nanjing University of Science and Technology,Nanjing 210094,China
2Laboratory of Computational Physics,Institute of Applied Physics and Computational Mathematics,Beijing 100088,China
3Center for Applied Physics and Technology,MOE Key Center for High Energy Density Physics Simulations,College of Engineering,Peking University,Beijing 100871,China
Abstract A one-dimensional discrete Boltzmann model for detonation simulation is presented.Instead of numerical solving Navier-Stokes equations,this model obtains the information offlow field through numerical solving specially discretized Boltzmann equation.Several classical benchmarks including Sod shock wave tube,Colella explosion problem,and one-dimensional self-sustainable stable detonation are simulated to validate the new model.Based on the new model,the influence of negative temperature coefficient of reaction rate on detonation is further investigated.It is found that an abnormal detonation with two wave heads periodically appears under negative temperature coefficient condition.The causes of the abnormal detonation are analyzed.One typical cycle of the periodic abnormal detonation and its development process are discussed.
Key words:detonation,discrete Boltzmann model,negative temperature coefficient,abnormal detonation
1 Introduction
Detonation is one kind violent combustion mode accompanied with a large amount of heat release within a short time.[1]It can be treated as a shock wave driven by chemical reaction and propagates with a supersonic speed.[2]Detonation is closely related to the energy use and production safety.
In some cases,it is necessary to generate detonation waves to improve the utilization efficiency of fuels.Because detonation possesses an approximate isovolumetric characteristic during chemical reaction,it has a higher mechanical efficiency than the general combustion mode.[3]Based on the detonation mechanism,several kinds of aeroengines conception including pulse detonation engine,[4]rotating detonation engine,[5]oblique detonation ramjetin-tube,[6]etc.have been presented and well investigated recently.While in other cases,the formation of detonation should be avoided as far as possible such as in coal mines.[7]Detonation is closely related to both the industrial production and our daily life.However,there still exists much unknown for its deep formation and propagation mechanisms.[3,8]
It has been well known that combustion and detonation are complex chemical reaction processes with various non-equilibrium behaviors including Hydrodynamic Non-Equilibrium(HNE),Thermodynamic Non-Equilibrium(TNE)and chemical reaction non-equilibrium.[9−10]For detonation research,traditional methods are mainly by using Navier-Stokes(NS)equations to describe the flow behaviour and using phenomenological reaction rate formula to describe the reaction process.[11]In addition,high resolution difference schemes are often needed to track the detonation interface and improve the numerical accuracy.[12−13]Of course,great progress has been made on the studies of detonation by the traditional method,especially in recent years.[3,9]However,NS equations themselves are not sufficient in describing the non-equilibrium effects in the reactive flow.The coefficients of viscosity and heat conduction in NS equations are generally calculated by empirical formula,such as Sutherland equation,or measured by experiments.[14−15]This method is not accurate enough when simulating the flow phenomena with strong non-equilibrium characteristics.Compared with NS equations,Boltzmann equation is more fundamental to describe the flow process.Rooted from the non-equilibrium statistic mechanics,Boltzmann equation is a mesoscale model and contains more kinetic information.By means of the Chapman-Enskog analysis,[16]a well-known multi-scale asymptotic expansion,the Euler equations can be obtained from the Boltzmann equation when the system is exactly in its local thermodynamic equilibrium state,and the NS equations can be obtained when the system linearly,in the Knudsen number,deviates from its local thermodynamic equilibrium state.However,when the system deviates much farther from its local thermodynamic equilibrium state,NS equations will not be accurate enough and fail to capture many important flow behaviors,whereas the Boltzmann equation naturally adapts to all of the above situations.
Unfortunately,the original Boltzmann equation is too complex to be solved directly,and some attempts have been made to simplify this model,among which the Lattice Boltzmann Model(LBM)[17−20]is a typicalone. ThefirstLBM forcombustion simulation was presented by Succi in 1997.[21]Subsequently,Filippova,[22]Yamamoto,[23]Chiavazzo,[24]Chen[25]and other researchers further developed the application of LBM to combustion simulation.However,all of those previous works aim only at simulating incompressible combustion and cannot satisfy the requirements of detonation simulation which shows pronounced compressible behaviors.Recently,Xu’s group made some attempts in simulating high speed compressible flows using LBM and developed it into a kinetic modeling method to investigate non-equilibrium characteristics.[26−30]To distinguish from the LBM aiming at numerical solving partial di ff erential equations,the kinetic modeling LBM is referred to simply as discrete Boltzmann method/model(DBM).Discrete Boltzmann method now has been well developed and widely used in various complex flow simulations including compressible flows,[31]multiphase flows,[32]Rayleigh-Taylor instability,[33−34]combustion and detonation.[35−38]The new observations brought by DBM are helpful to understand the mechanisms for formation and e ff ects of shock wave,phase transition,energy transformation,and entropy increase in various complex flows. Besides by theory,results of DBM have been con firmed and supplemented by results of molecular dynamics,[39−41]direct simulation Monte Carlo[42−43]and experiment.[44]In the system containing both material interface and mechanical interface(such as shock wave and rarefaction wave),non-equilibrium characteristics have been used to recover the main feature of real distribution function,and to provide physical criteria for discriminating various interfaces. The latter has been used to design appropriate tracking schemes for various interfaces.[28,33,45−46]In recent studies,[34,47]the correlations between the various macroscopical nonuniformity and the relevant non-equilibrium strengths in systems with Rayleigh-Taylor instability and/or Richtmyer-Meshkov instability are used to probe the material mixing processes.In 2013,the first DBM for detonation was presented[35]then a series of extensions have been made.For example,the Multiple-relaxation-time DBM[38,48]and double-distribution-function DBM[36]have been developed.However,those works are all two-dimensional model and at least 16 discrete velocities are needed.[37]The calculation efficiency is much low for some cases where the main behaviors can be described by one-dimensional model.In those cases,a one-dimensional DBM model for detonation is in demand.
Generally speaking,during a combustion process,many species of reactants and a large number of reactions are involved.For example,the combustion of CH4in air involves 53 species and 325 reactions.[49]The reaction rate varies with the special reaction paths.A detonation process may guide the reactions into different reaction chains because of the type of fuel,shock strength,premixing homogeneity,etc.Consequently,the global reaction rates show different behaviors for different conditions and may possess a non-monotonic dependence on the temperature.Although most of the reaction rates have an exponential temperature dependence and the Arrhenius model is commonly be adopted to describe the reaction rate,the phenomenon of Negative Temperature Coefficient(NTC)in reaction rate has been observed in combustion process and has drawn great attention in recent years.[9,50−51]The existence of NTC may also cause significantly special phenomena during the detonation process.However,to the authors′knowledge,possible effects of NTC on detonation have not been well studied.In 2016,we conducted a preliminary study on the effects of NTC during detonation.[37]In that work,we found that the effect of NTC during detonation is to lower the reaction rate and delay the formation of detonation wave.In this paper,we further study the characteristics of detonation under NTC based on the one-dimensional DBM.An abnormal detonation phenomenon with two wave heads is observed and carefully studied.
2 Model and Verification
2.1 Discrete Boltzmann Model and Chemical Reaction Rate Model
For the one-dimensional discrete Boltzamnn model,the evolution of the distribution function fifor the discrete velocity viis governed by Eq.(1),
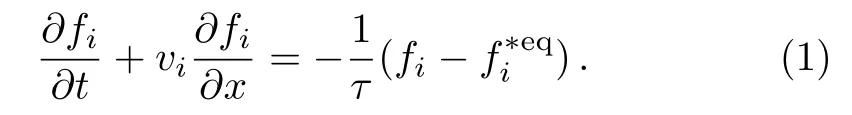
The subscript i in fiindicates the index of discrete velocity vi.The variables,t and x,are the time and spatial coordinates,respectively,and τ is the relaxation parameter.is the local equilibrium distribution function taking into account the effects of chemical reaction and can be calculated by
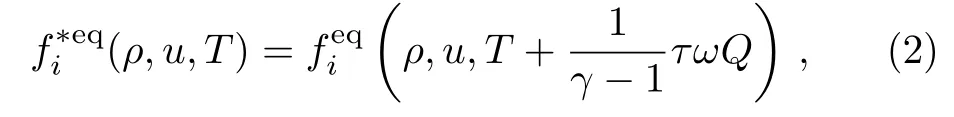
where ρ,u,and T are the density,velocity,and temperature,respectively.γ is the ratio of special heats,ω is the chemical reaction rate,and Q is the amount of heat release per unit mass of reactant.Theon the right-hand of Eq.(2)can be solved by the following seven equations:


where ηiis a free parameter introduced to describe the n extra degrees of freedom corresponding to molecular rotation and/or vibration.[27]In this paper ηi= η0for i=1,2,3 and ηi=0 for i=4,5,6,7.
From multi-scale asymptotic expansion,we know that NS equations with chemical reactions,Eqs.(10)–(12),can be deduced from Eq.(1)under the conditions of Eqs.(3)–(9).
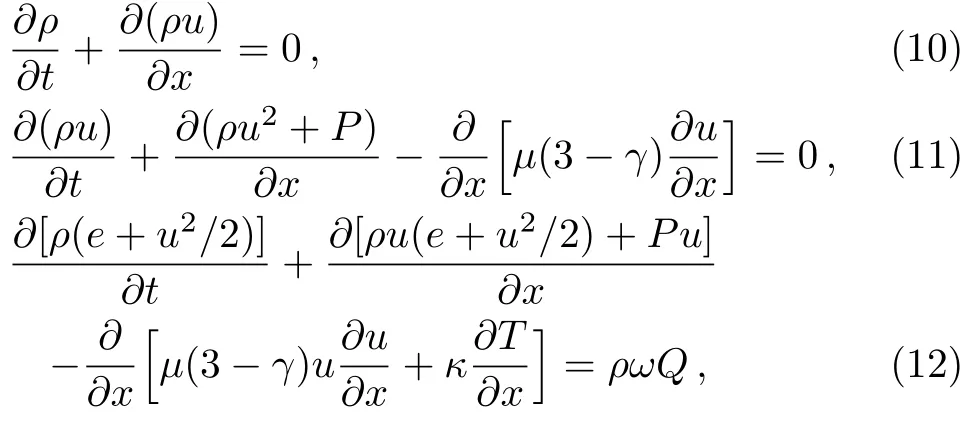
where P=ρT is the pressure,e=(n+1)T/2 is the internal energy density, µ = τρT and κ =cpτρT are the coefficients of viscosity and heat conduction,respectively,the constant-pressure specific heat is cp=(n+3)/2 and the specific heat ratio is γ=(n+3)/(n+1).

Fig.1 Discrete velocity model for one-dimensional DBM.

Table 1 Values of discrete velocities.
In order to solve the above seven equations,at least seven velocities are needed.The discrete velocities model adopted in this paper is shown schematically in Fig.1.The corresponding values of discrete velocities are listed in Table 1 and c0is a free parameter depends on the numerical stability.
The chemical reaction rate ω is described by
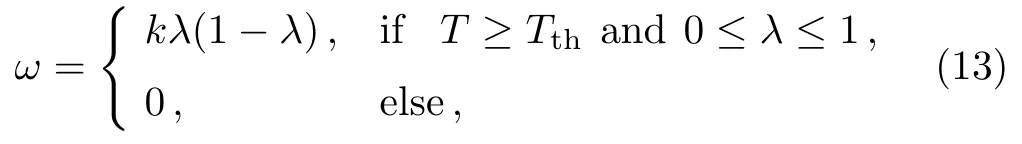
where k is reaction rate constant and λ indicates reaction process.It has λ=0 at the beginning of the reaction and λ=1 at the end of the reaction.Tthis defined as ignition temperature and there is no reaction happens below this threshold value.
In addition to being able to recover to NS equations with chemical reactions,DBM provides a set of non-equilibrium measurements,which is also its advantage over the traditional hydrodynamic model.The nonequilibrium quantities are represented by the difference between the moments of distribution function and its corresponding local equilibrium distribution function at a certain time.Those non-equilibrium quantities are defined as
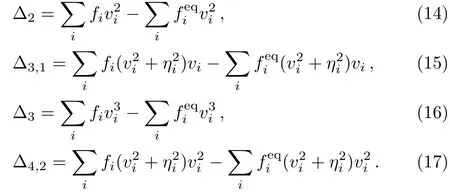
Another set of non-equilibrium quantities can also be defined by the kinetic center moment in a similar way.Each of those quantities re fl ects the non-equilibrium characteristic of system from a di ff erent perspective which cannot be provided by the traditional hydrodynamic model.Those non-equilibrium quantities are signi ficant around the detonation wave front because of the e ff ects of impact compression and chemical reactions.
2.2 Model Verification
In order to validate the new model,several typical benchmarks are carried out.Firstly,two shock wave problems,including the Sod shock tube and Colella explosion wave problem,are simulated and compared with the Riemann solutions.Then a one-dimensional self-sustainable stable detonation is simulated and compared with CJ theoretical solutions.
(i)Sod Shock Tube Test
Sod shock tube is a well benchmark and has been widely used to test the ability of processing discontinue for a numerical model.The initial conditions are
(ρ,u,T)L=(1,0,1), (ρ,u,T)R=(0.125,0,0.8),(18)where the subscripts“L” and “R” indicate the left half region and right half region,respectively.Simulation is carried out under the conditions:τ=2×10−5,∆x=2× 10−4,Nx=5000,∆t=5× 10−6.c0=1.2 and η0=3 are chosen to ensure numerical stability.Besides,it has n=4 so that γ=1.4.The free in flow and outflow boundary conditions are adopted in left and right boundaries,respectively,which means fi,−1=fi,0=fi,1and fi,Nx+2=fi,Nx+1=fi,Nx.In order to solve the space derivation and the time derivation in Eq.(1),the second-order nonoscillatory non-free-parameter and dissipative(NND)[52]scheme and the first-order forward difference scheme are used,respectively.Figure 2 shows the comparison of the DBM results and Riemann exact solutions at t=0.22.From Fig.2 we can see that the DBM results are well consistent with the exact solutions,so the new model can well process discontinuity in the flow field.

Fig.2 Comparisons between DBM results and exact solutions for Sod shock tube test.(a)density ρ,(b)temperature T,(c)pressure P,(d)velocity u.The solid lines and symbols are the Riemann solutions and DBM results,respectively.
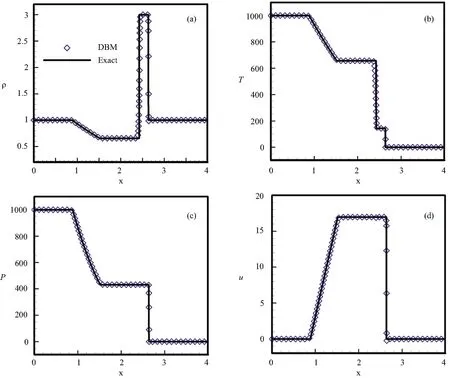
Fig.3 Comparisons between DBM results and exact solutions for Colella explosion wave test.(a)density ρ,(b)temperature T,(c)pressure P,(d)velocity u.The solid lines are Riemann solutions and symbols indicate DBM results.
(ii)Colella Explosion Wave Test
Colella explosion problem is another challenging test to examine the numerical stability and precision of a model.The initial conditions are

The simulation conditions are τ=1× 10−5,∆x=2× 10−3,Nx=2000,∆t=5× 10−6,and n=4(i.e.,γ =1.4).Besides,it has c0=20 and η0=16 so that the calculation is stable.The boundary conditions and difference schemes are the same with those in Fig.2.Simulation results at t=0.025 are shown in Fig.3 and the exact solutions based on Riemann analysis are also plotted for comparison.The solid lines are Riemann solutions and symbols indicate DBM results.The simulations and the exact solutions are very consistent,from which we can conclude that the new DBM is applicable to simulate flows with very high ratios of temperature(up to 105).
(iii)Self-sustainable Stable Detonation
As the last test,a one-dimensional self-sustainable stable detonation is simulated.Considering that there is a rigid tube full of premixed combustible gas and the initial condition in this tube is set as
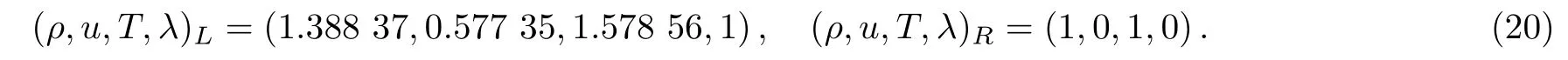
Parameters are set as τ=2×10−5,∆x=2×10−4,Nx=5000,∆t=5×10−6,and n=4(i.e.,γ =1.4).In order to ensure the numerical stability,it has c0=2 and η0=2.The chemical reaction rate is given by Eq.(13)and k=2000.The left boundary is set as fixed wall while the right boundary is set as outflow.The difference schemes are the same with those in Fig.2.From Fig.4(a),we can see that the self-sustained detonation with a stable wave speed is formed.Then the macroscopic quantities at sound velocity surface behind the detonation wave front are compared with the CJ theoretical values.The corresponding values are shown in Table 2 and it shows that relative errors are all less than 5.43%.So,it can be concluded that the new DBM can be used to investigate the one-dimensional detonation problem.
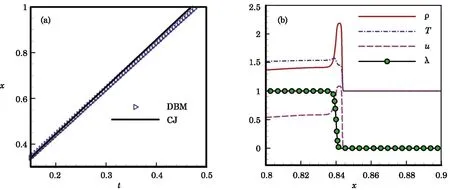
Fig.4 Simulation results of self-sustained stable detonation.(a)the position of von Neumann peak of pressure where the solid line is CJ theoretical solution and the symbol is DBM result.(b)the macroscopic quantities(density,temperature,velocity,and reaction process)profiles at t=0.4.
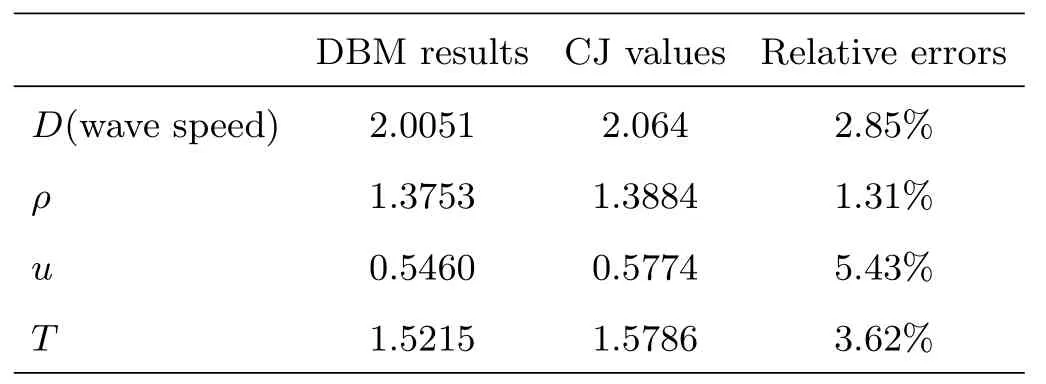
Table 2 Comparisons between DBM results and CJ theoretical values for stable detonation.
3 An Abnormal Detonation Induced by Negative Temperature Coefficient
3.1 Simulation of the Abnormal Detonation
In order to investigate the NTC of chemical reaction rate,we adopt the following formula to describe the temperature dependence of rate constant k in Eq.(13)which has been presented in Ref.[37].
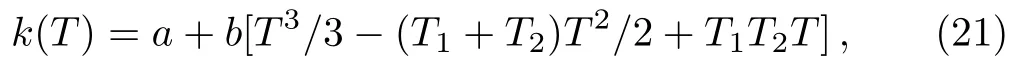
with
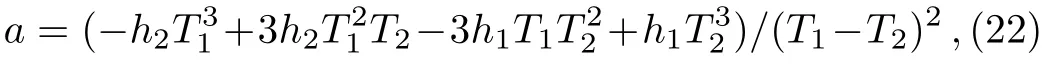

where h1and h2are the peak and valley value of k,respectively.T1and T2are values of temperature corresponding to h1and h2,respectively.In this work,we set h1=2000,h2=10,T1=1.14,T2=1.45.Besides,the ignition temperature in Eq.(13)is set as Tth=1.1.The rate constant-temperature curve is shown in Fig.5.It can be clearly seen that there is an NTC interval where the reaction rate constant decreases with the increase of temperature.
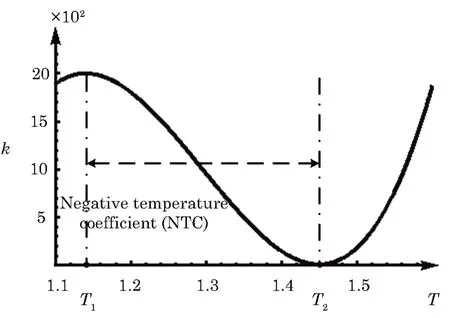
Fig.5 Relation curve of rate constant with temperature.
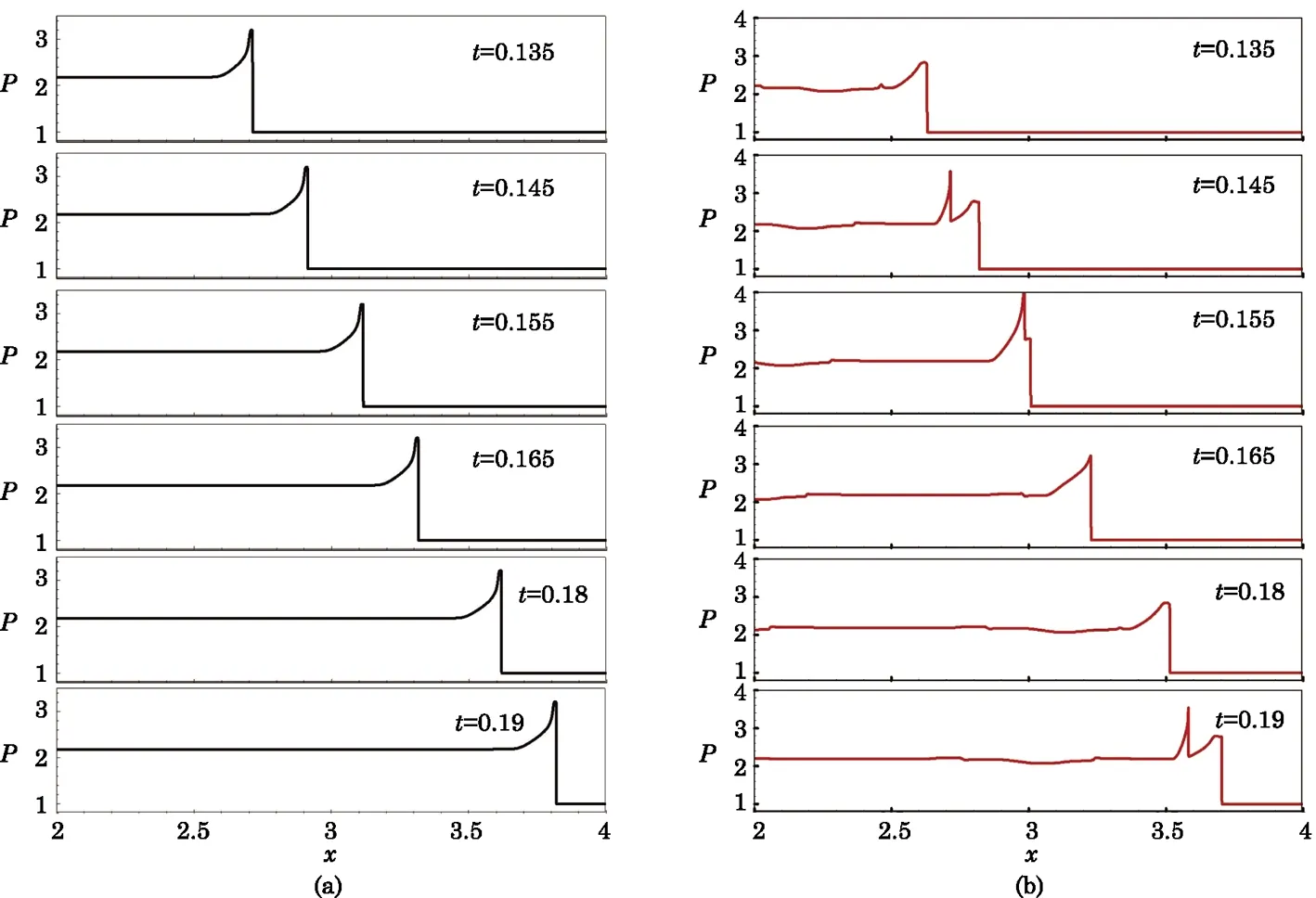
Fig.6 Comparisons between(a)the normal detonation wave and(b)the abnormal detonation wave.
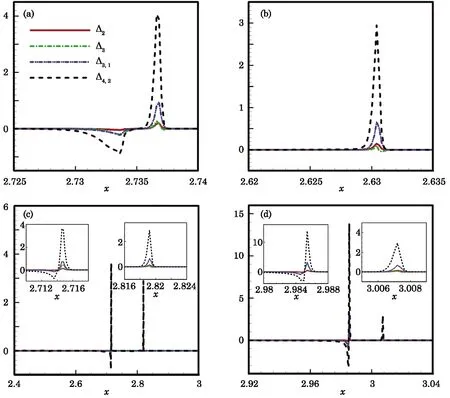
Fig.7 Profiles of non-equilibrium quantities for(a)normal detonation,(b)abnormal detonation at t=0.135,(c)abnormal detonation at t=0.145,and(d)abnormal detonation at t=0.155.
Except the chemical reaction rate and Nx=50000,other simulation conditions are all the same with those in Fig.4.Under this chemical reaction condition,an abnormal detonation phenomenon is obtained,which is shown in Fig.6(b).The normal stable detonation processes with a constant speed and a stable waveform are also shown in Fig.6(a)for comparison.For the abnormal detonation,there is no constant wave speed and the waveform changes with time periodically.Figure 6(b)gives the evolution of the waveform in one cycle.Firstly,at a certain time,a local hotspot is generated behind the wave head.Then a local detonation wave appears and develops with a speed faster than its downstream wave front.So the new formed detonation wave chases the front wave and finally the two waves merge into an over-driven detonation wave.However,the over-driven detonation wave cannot self-sustain,so the wave velocity gradually decreases until it reaches the CJ detonation wave velocity.After that,a local hotspot generates again and a new cycle begins.
The corresponding non-equilibrium quantities∆2,∆3,∆3,1,and ∆4,2defined in Eqs.(14)–(17)are plotted in Fig.7.For the normal detonation shown in Fig.6(a),the shape of the wave front does not depend on time so the non-equilibrium characteristics around the wave front keep unchange with time.The profiles of∆2,∆3,∆3,1,and∆4,2for the normal detonation are given in Fig.7(a).It can be seen the system deviates from the equilibrium in the opposite direction at two sides of the wave front.In fact,it has been known that the nonequilibrium quantities are close to zero near the von Neumann peak point.[28,35]However,for the abnormal detonation,the pro files of non-equilibrium quantities vary with time. Figures 7(b),7(c),and 7(d)give the profiles of non-equilibrium quantities for the abnormal detonation at three typical moments.From Fig.6,we can see the wave front of the abnormal detonation is very similar to the normal detonation at t=0.135 but the pro files of non-equilibrium quantities in Fig.7(b)and those in Fig.7(a)are much di ff erent.The non-equilibrium deviations in Fig.7(b)are always in the same direction.From Figs 7(c)and 7(d)which correspond to t=0.145 and t=0.155,respectively,double wave fronts can be observed.The non-equilibrium characteristics around the back detonation wave(the left wave)is very similar to those in Fig.7(a)and the non-equilibrium characteristics around the front detonation wave(the right wave)is similar to those in Fig.7(b).In addition,the non-equilibrium strength is more significant for the abnormal detonation than the normal detonation when two wave fronts exist.
3.2 Analysis and Discussion about the Abnormal Detonation
In this section,we will discuss the causes of the abnormal detonation wave.For convenience,we roughly divide the reaction into three stages according to the temperature.Those three stages are denoted as S1,S2,and S3,respectively,as shown in Fig.8.The first stage(S1)is in the low temperature region but has a fast reaction rate because of NTC.The second stage(S2)has a slower reaction rate at a specific temperature range.The third stage(S3)has a fast reaction rate at high temperature and the reaction rate increases dramatically with the increment of temperature.
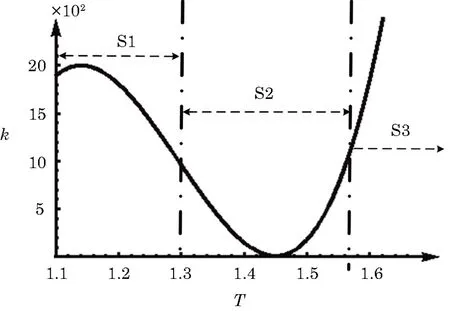
Fig.8 Three stages of chemical reaction rate.
The development of the abnormal detonation is shown in Fig.9.At t=0.12,as shown in Fig.9(a),the detonation wave is still a normal detonation followed by a long rarefaction wave region.The temperature behind the wave head has not reached the third stages(S3).So it has only the first two stages,S1 and S2,of the chemical reaction.At t=0.13,as shown in Fig.9(b),a local hotspot appears in the rarefaction wave region and the temperature in this hotspot achieves to S3,then the third stage of chemical reaction appears.Because it has a rapid reaction rate in S3,a local detonation wave is formed and developed quickly.The local detonation wave moves forward and obtains more fuel,so it continues being strengthened and has an increasing wave speed.From Fig.9(c)we can see S3 gradually widens while S2 becomes narrower.At t=0.15,the new formed detonation wave almost catches up with the front detonation wave.At this time,S2 is nearly disappeared,which can be seen from Fig.9(d).After that,two waves merge and the overdriven detonation occurs.
The evolution of the process from overdriven detonation to the normal detonation is shown in Fig.10.Fig.10(a)shows the overdriven detonation wave at t=0.155,which has a wave speed faster than the CJ detonation.At this time,almost all of the chemical reactions occur in S3.However,overdriven detonation cannot selfsustain and rarefaction waves would gradually form behind the wave head.At t=0.165,as shown in Fig.10(b),the temperature behind the detonation wave front begins to go down due to the effect of the rarefaction waves.When the temperature goes down to the region of S2,the second stage of the chemical reaction occurs.Then the rarefaction waves behind the wave head continue growing and temperature behind the wave keeps going down.When the temperature declines to the region of S1,the first stage of reaction occurs.As more and more fuel reacts in S1 and S2 reactions occur in S3 gradually decrease,which can be seen from Figs.10(c)and 10(d).As a result,the overall reaction rate slows down.With the chemical reaction rate slows down,the detonation wave speed gradually decreases to CJ detonation wave speed.After that,a local hotspot reappears and a new local detonation wave is developed again,which means the above process is repeated.The whole process of the development of the abnormal detonation within a period can be summarized by Fig.11.
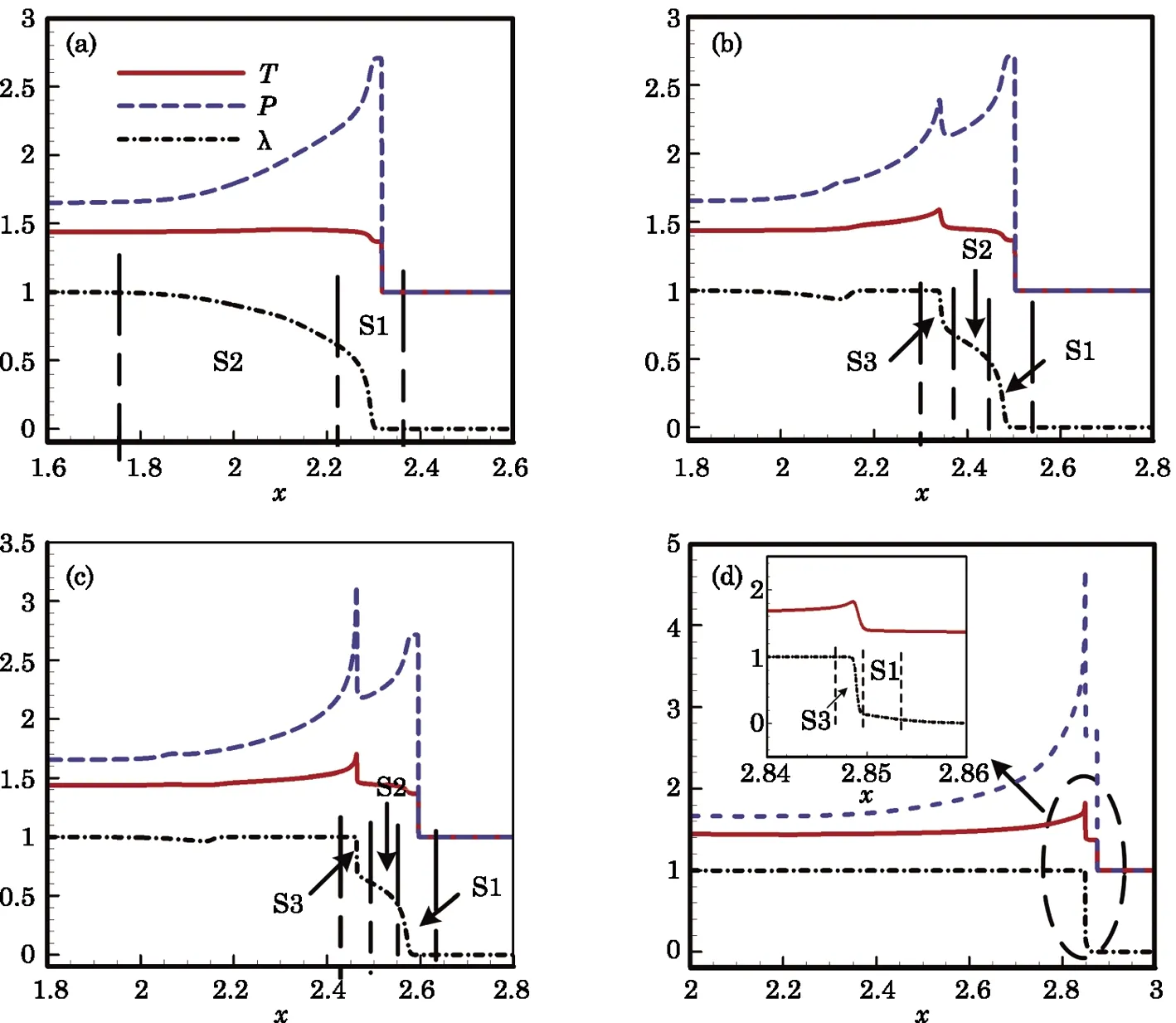
Fig.9 Detonation waveforms at(a)t=0.155,(b)t=0.165,(c)t=0.175,and(d)t=0.18.
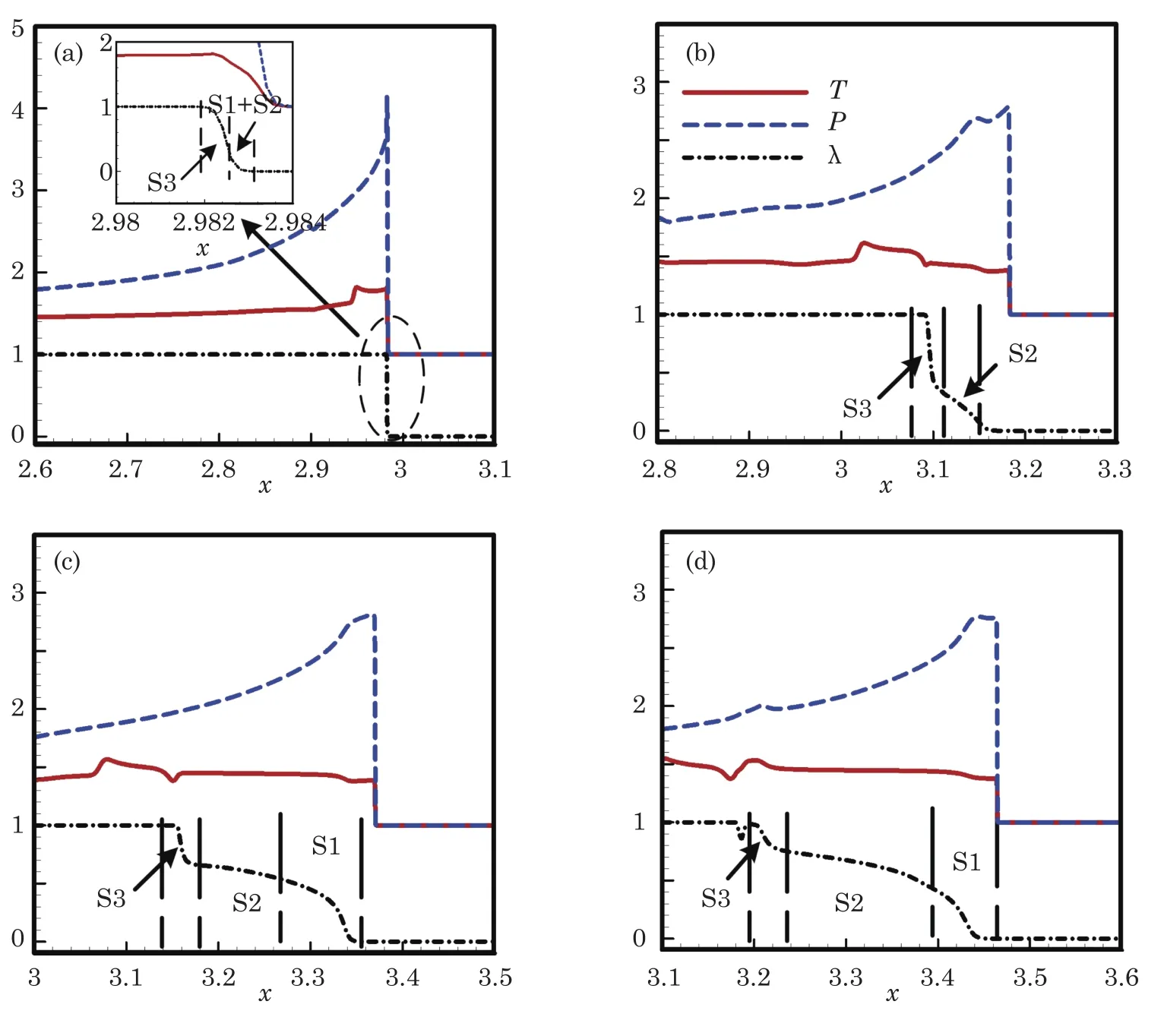
Fig.10 Detonation waveforms at(a)t=0.155,(b)t=0.165,(c)t=0.175,and(d)t=0.18.
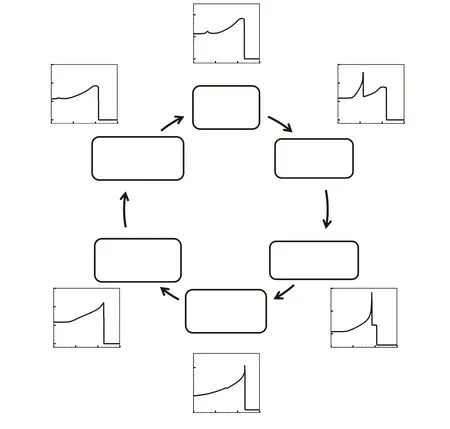
Fig.11 Schematic diagram of development process of the abnormal detonation.
4 Conclusion
In this work,we present a one-dimensional discrete Boltzmann model for detonation.The validity of the new model is veri fied by three tests.The new detonation model possesses both high computational efficiency and numerical accuracy.Based on the new model,the e ff ects of negative temperature coefficient of reaction rate in a detonation are further investigated.An abnormal detonation phenomenon is presented and its development process is analyzed.It is found that the main reason for the abnormal detonation is that the chemical reaction has three stages,namely S1,S2,and S3.The first stage,S1,is in the low temperature region but has a fast reaction rate,the second stage,S2,has a slower reaction rate at a specific temperature range,and the third stage,S3,has a fast reaction rate at high temperature and the reaction rate increases dramatically with the increase of temperature.For a normal detonation,the chemical reactions occur mainly in S1 and S2.For the abnormal detonation,however,at a certain time a local hotspot is formed as a consequence of the S3.Then a new detonation with a more violent chemical reaction appears behind the old detonation wave front.The new detonation wave has a faster speed than the wave ahead,it catches up with the front wave and f inally two waves merge.Then the speed of the detonation wave begins to slow down until it reaches a CJ detonation value.After that,the local hotspot appears again and the previous process reappears.
杂志排行
Communications in Theoretical Physics的其它文章
- Kinetic Simulation of Nonequilibrium Kelvin-Helmholtz Instability∗
- Nontrivial Effect of Time-Varying Migration on the Three Species Prey-Predator System∗
- Impact of Colored Noise on Population Model with Allee Effect∗
- Improved Five-Parameter Exponential-Type Potential Energy Model for Diatomic Molecules∗
- Dynamically Tunable and High-Contrast Graphene-Based Terahertz Electro-Optic Modulator∗
- Multipolar Structure of Equilibrium Shear Flow Field in Toroidal Plasmas∗
