Improved Five-Parameter Exponential-Type Potential Energy Model for Diatomic Molecules∗

Ke-Xue Fu(付珂雪),Meng Wang(王萌),and Chun-Sheng Jia(贾春生)

1Chengdu Shishi High School,Chengdu 610000,China

2Xindu No.1 Middle School,Chengdu 610500,China

3State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation,Southwest Petroleum University,Chengdu 610500,China

Abstract The dissociation energy and equilibrium bond length as explicit parameters are used to establish an improved five-parameter exponential-type potential energy model for diatomic molecules.We demonstrate that the five-parameter exponential-type potential is identical to the Tietz potential for diatomic molecules.It is observed that the improved five-parameter exponential-type potential can well model the internuclear interaction potential energy curve for the ground electronic state of the carbon monoxide molecule by the utilization of the experimental values of three molecular constants.

Key words:interaction potential energy,improved five-parameter exponential-type potential,carbon monoxide

1 Introduction

The knowledge of internuclear interaction potential energy between two atoms as a function of their relative positions is of fundamental importance in a wide variety of fields.There has been a growing interest in obtaining an available closed-form representation governing the interaction of two atoms for diatomic molecules in chemistry and physics.Numerous contributions have been made to build analytical internuclear potential energy functions.[1−15]In recent years,by utilizing the dissociation energy and equilibrium bond length for a diatomic molecule as explicit parameters,some authors[16−21]constructed improved versions with more convenient applications for some empirical potential energy functions,including the well-known Rosen-Morse,Tietz,Frost-Musulin,Manning-Rosen,and Pschl-Teller potentials.The improved molecular potentials have received considerable attentions due to their real applications in many fields,including simulations of molecular potential curves,predictions of thermochemical quantities of gaseous substances,and calculations of molecular vibrational energies.[21−50]There has been an increasing recognition of the importance of the Tietz potential as a typical potential energy model.Hassanabadi et al.[51−53]studied the solutions of the Dirac equation and Klein-Gordon equation with the Tietz potential in terms of the supersymmetry quantum mechanics approach.Ikot et al.[54]investigated the bound state solutions of the Duffin-Kemmer-Petiau equation with the Tietz potential by employing the Nikiforov-Uvarov method.Onate et al.[55]computed the Shannon entropy and information energy under the modified Tietz-Hua potential.Khordad and Mirhosseini[56]studied the optical properties of spherical quantum dots by using the Tietz potential.

In 2001,the authors in the literature[12]proposed a five-parameter exponential-type potential model,and obtained a general energy spectrum formula by solving the Schrdinger equation with that in terms of the supersymmetry shape invariance approach.By choosing suitable forms of the parameters,the five-parameter exponentialtype potential can turn to some well-known potential functions,including the Hulth´en potential,Eckart potential,and improved Manning-Rosen potential.It is unfortunate that the model parameters in the five-parameter exponential-type potential lack explicit physical definitions.This fault has greatly affected its effective applications.In this work,we attempt to establish an improved five-parameter exponential-type potential energy model for diatomic molecules,and explore the relationship between it and the well-known Tietz potential in the presence of a diatomic molecule.We also apply the improved five-parameter exponential-type potential to model the internuclear interaction potential curve for the ground electronic state of the carbon monoxide(CO)molecule.A great deal of CO is released from tail gases,including coke oven gas,carbon black manufacturing tail gas,etc.CO is one of the most prominent gaseous environment pollutants,and a highly toxic gas for humans as well as for animals.Due to its high harmful effect on human health,the adsorption processes of CO in various adsorbent materials have aroused considerable attention.[57−61]

2 Improved Five-Parameter Exponential-Type Potential Energy Model

The five-parameter exponential-type potential energy model can be represented as Eq.(1),[12]

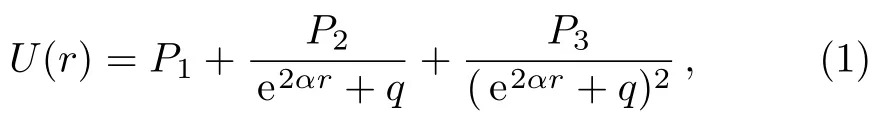
where P1,P2,P3,q,and α are five adjustable parameters,and q̸=0.

For a diatomic molecular potential energy function U(r),it is directly related to the three molecular constants and satisfies the following three relationships:

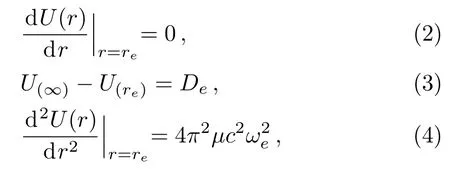
where Dedenotes the dissociation energy for a diatomic molecule,reis the equilibrium bond length,ωerepresents the equilibrium harmonic vibrational frequency,µis the reduced mass of the molecule,and c is the speed of light.Taking the first order derivate of U(r)with respect to the r variable and substituting it into Eq.(2),we obtain

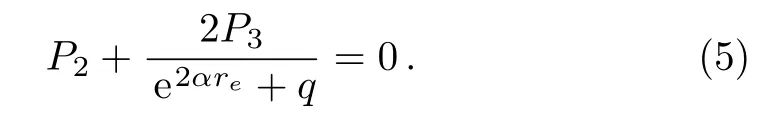
From Eq.(5),we have the following expression,

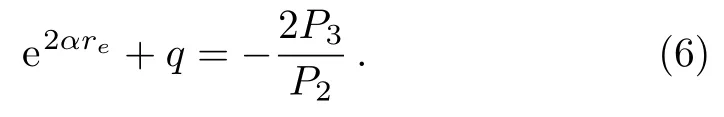
With the help of expression(6),we obtain the following relationship from Eq.(3),

Solving Eqs.(6)and(7)for parameters P2and P3yields the following two expressions,

Substituting expressions(8)and(9)into Eq.(1)and making simple algebraic manipulations,we can rewrite potential function(1)in the following form

In order to achieve a choice that the minimum value of the potential energy is zero,i.e.U(re)=0,an additional term of De−P1is added to the right hand of expression(10).This manipulation does not produce any change in the physical properties of the original potential energy function.The five-parameter exponential-type potential function can be further represented as the following form

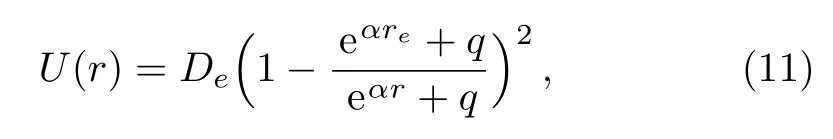
here we have replaced α by α/2 for the sake of simplification.The improved five-parameter exponential-type potential given in the above expression is just the improved Tietz potential.[16]Therefore,the five-parameter exponential-type potential is identical to the Tietz potential for diatomic molecules.Employing the improved Tietz potential to represent the internal vibration of a molecule,the molar entropy values have been satisfactorily predicted for gaseous substances,including the gases CO,HCl,HF,DF,NO,and gaseous BBr.[30]Choosing q=0,the improved five-parameter exponential-type potential becomes the standard Morse potential.[1]When q=1 and q=−1,the improved five-parameter exponential-type potential turns to the standard improved Rosen-Morse potential[16]and improved Manning-Rosen potential.[18]

We calculate the second order derivation of U(r)given in expression(11)with respect to r,and substitute it into Eq.(4).In the presence of given parameter q,we solve Eq.(5)for parameter α and achieve the following expression,

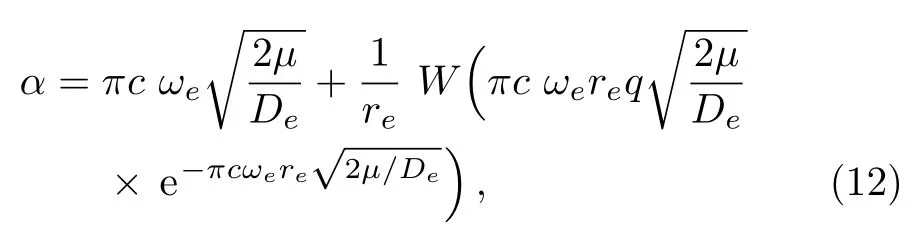
in which W represents the Lambert W function,which satisfies z=W(z)eW(z).[62]

3 Applications

By choosing an available value of parameter q and putting the experimental values of the molecular constants De,re,and ωeas inputs,we reproduce the potential energy curve for the ground electronic state of CO in terms of the improved five-parameter exponential-type potential. The experimental values of three molecular constants are obtained by referring to the literature:[13]De=90 670cm−1,re=1.128 323 20 ˚A,and ωe=2169.8129cm−1.Substituting these values into expression(12)and taking q=−0.55,we obtain the value of parameter α as α =2.191 89 ˚A−1.The variation of internuclear interaction potential with internuclear distance is shown in Fig.1,in which the green solid line stands for the predicted values and red solid circles represent the experimental Rydberg-Klein-Rees(RKR)[63−65]data points from the literature.[66]Figure 1 shows that the predicted potential energy values are in excellent agreement with the experimental RKR potential data points over the entire interaction distance range except at much large r.

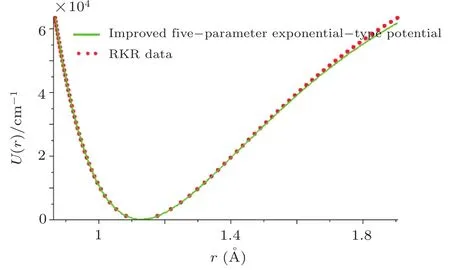
Fig.1 Experimental RKR data points and the improved five-parameter exponential-type potential energy curve for the ground electronic state of CO.

In order to evaluate quanti ficationally the accuracy of the proposed potential,we consider the average absolute deviation of the improved five-parameter exponentialtype potential versus the experimental RKR potential.The average absolute deviation is represented as σav=100here Npdenotes the number of experimental data points considered in the RKR potential,URKR(r)and Ucalc(r)represent the experimental RKR potential and the empirical analytical potential,respectively.The average deviation of the improved five-parameter exponential-type potential versus the RKR potential reported by Kirschner,and Watson[66]is 0.333%of De.This average absolute deviation satisfies satisfactorily the Lippincott’s error criterion for an available empirical closed-form potential energy representation.The Lippincott’s error criterion implies that an average absolute deviation should be less than 1%of the dissociation energy for a successful analytical energy function.[10]

4 Conclusion

Through the introduction of the dissociation energy and equilibrium bond length as explicit parameters,we establish the improved five-parameter exponential-type potential model for diatomic molecules.We show exactly and simply that the five-parameter exponential-type potential is identical to the Tietz potential in the presence of a diatomic molecule.Using the experimental values of the dissociation energy,equilibrium bond length and equilibrium harmonic vibrational frequency,we model satisfactorily the potential energy curve for the ground electronic state of CO.By the calculation of average absolute deviation of the proposed potential versus the experimental RKR potential,we show quantitatively that the improved five-parameter exponential-type potential is an available model to represent the internuclear interaction potential for the ground electronic state of the CO molecule.

Acknowledgements

We would like to thank the kind referee for positive and invaluable suggestions which have greatly improved the manuscript.