基于图像分块稀疏表示的人脸识别算法研究
2019-01-10陈晖
陈 晖
(福建信息职业技术学院 计算机工程系,福州 350001)
基于稀疏表示的分类算法,经过一系列的研究与实验,被成功应用于人脸识别系统的构建过程中,基本原理就是将测试样本图像表示为训练样本的线性组合.这种方法的应用,使得人脸识别技术能够更好的应对光照、表情变化以及部分遮挡等对识别效果造成的不良影响,显示出较高的鲁棒性.另有Deng等人,基于这种分类算法,提出了一种原型加变差的表示模型,对单样本人脸识别的问题进行了有效解决,而本文则在此基础上,将其与分块处理思想融合,强化局部特征的作用,从而提升技术应用效果.
1 基于稀疏表示的人脸识别算法概述
基于稀疏表示的人脸识别算法,首先要进行字典的构造,完备字典的基本元素,就是训练集本身;然后进行测试样本以及稀疏表示分类,当每一类都具有足够的训练样本时,通过同类别的样本的线性组合,即可对测试样本进行表示,最终得到最稀疏的测试样本的线性组合;将最稀疏的测试样本的线性组合,通过最小l1范数进行重购;最后通过随机特征提取,进一步判断测试样本与各类之间的残差大小,从而有效确定识别标签[1].
充分利用稀疏表示的判别性,在人脸识别的过程中,任意的测试样本都可以从字典中的训练集表示获得,进一步通过稀疏系数求解残差,即可获得识别标签.字典的构造过程如下:
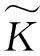
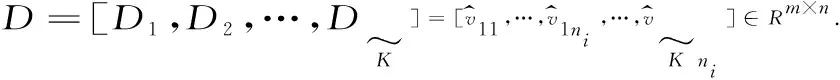
结合表示理论,能够进一步得到测试样本y的线性组合:

2 基于图像分块稀疏表示的人脸识别算法对比
2.1 基于非重叠分块的加权稀疏表示算法
在人脸识别技术的初期研究过程中,研究人员尝试采用了多种基于稀疏表示的衍生算法,但在一些特定的环境当中,如人脸图像连续性遮挡等,相关算法并不能对其进行有效处理.所以,在后续的研究中,研究人员转变技术方向,将稀疏表示分类(SRC)与人脸图像非重叠分块方法相融合.这一新的算法,可以实现将人脸图像进行非重叠式分块处理,进而对所得的数块图像,分别进行加权,最终重新构建一个新的人脸特征组合,确定识别标签.该算法的具体处理过程如下:
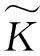
2)设计加权系数.将测试图片的模块视为字典中Ak的线性组合,即:yk=Akxk.这种表示方式是一种欠定系统,其目的就是获得一个稳定的、唯一的解.
算法运行过程中,需要同步加入l1和l2范数的约束条件,相应的优化问题,一般表示为:
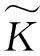
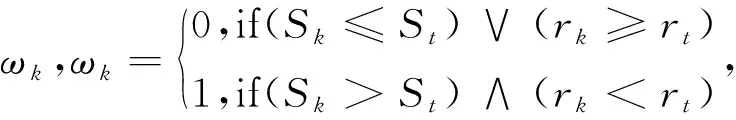

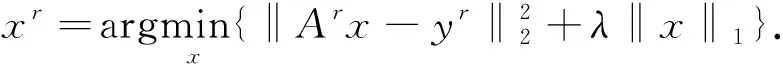
由此可见,基于非重叠分块的加权稀疏表示算法,能够缓解图片当中遮挡、光照或表情变化等所带来的识别不准确问题,相对于单一的基于稀疏表示的分类算法的人脸识别技术,相应的识别效果得到了一定的提升.
笔者将上述算法的运用效果,与现有的几种算法的应用效果进行了对比,在不同像素尺寸下,各个算法的识别率如表1所示.通过对比结果能够发现,当图像的尺寸增大到80*64时,其余算法的识别效果都相应提升,而模块加权算法自始至终,都能够保持较高的识别率.
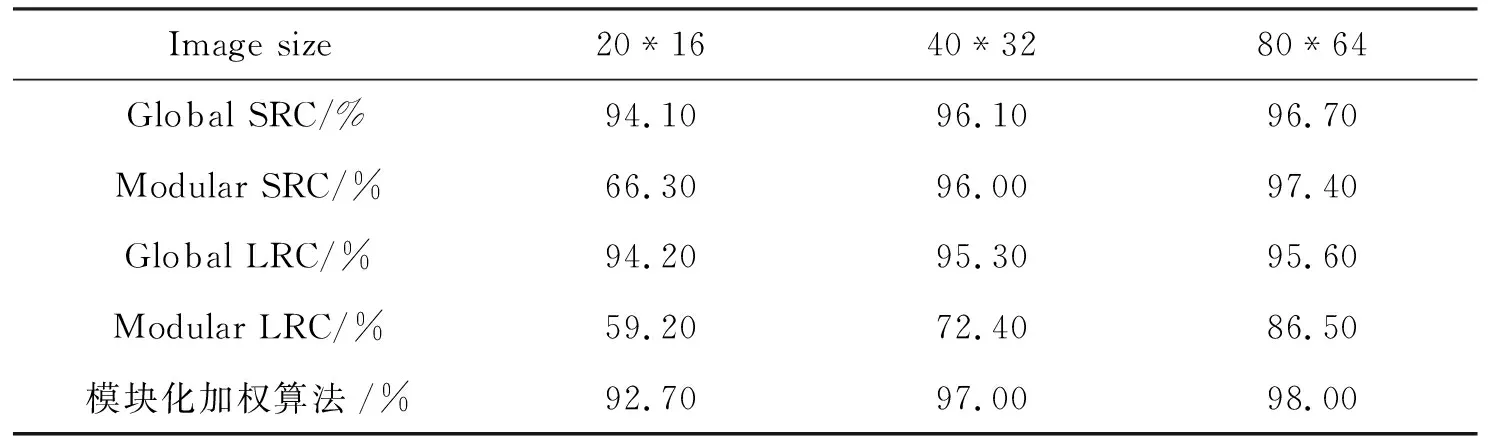
表1 不同像素尺寸下人脸识别算法的识别率
2.2 基于图像重构和哈希的人脸识别算法
基于图像重构的人脸识别方法的基本原理,即利用多输入图像之间的相关性,将目标图像进行重构,形成一幅更具代表性的图片.此时,随着训练数据或图像位数的增加,人脸识别算法的运算速率会大大降低.为此,引入哈希算法,将其与基于图像系数表示的人脸识别算法相融合,能够综合提升人脸识别效果与识别速度[2].
基于图像重构和哈希的人脸识别算法,主要涉及到三方面的工作内容如下:
1)组稀疏编码.针对这一问题,可以利用一组目标函数,来实现对分类问题的有效求解:
ζ(a,x;Y,D)=‖Ya-Dx‖2+λψ(x)
在算法应用过程中,从字典当中获取的测试样本为y1,y2,…,yk;Y=[y1,y2,…,yk].a表示k维的向量,且a=[a1,a2,…,ak]T,其中,a1+a2+…+ak=1,a1,a2,…,ak均大于0.x表示稀疏系数向量,且x≠0;D表示训练矩阵.
在算法运算过程中,向量a将多输入样本结合在一起之后,即可形成一个新的图像向量,新向量的维数等同于多输入样本的维数.

图1 图像不分块示意图
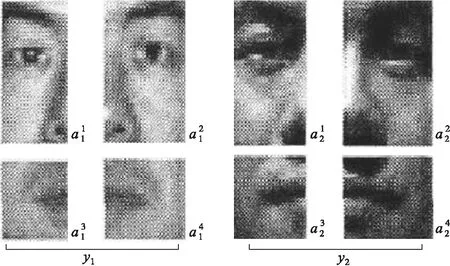
图2 图像分成4块示意图

运算实现时,可借助Hash矩阵,将最初获取到的高维数据矩阵,映射到一个低维的数据空间中,确保在新的环境中,数据仅为{0,+1,-1},在为算法的应用降低计算量的同时,也就相应提高了算法的运算效率[3].

2.3 基于低秩分块稀疏表示的人脸识别算法
基于低秩分块稀疏表示的人脸识别算法的核心,是一种新的结构不相关的低秩矩阵恢复方法.此外,还进一步结合了离散余弦变换方法.两种方法的综合运用,能够有效解决人脸识别过程中,人脸图像中存在的遮挡或光照等问题;算法运用过程中,还会采用一种重叠分块方法,主要作用是利用冗余信息提高算法的识别率;分类时所采用的alignment pooling的方法,也能在一定程度上提高算法的识别速度.
低秩矩阵恢复在解决稀疏噪声方面,具有较大的作用.利用低秩矩阵恢复技术,其主要目的是将训练集的数据矩阵D分解生成A+E的形式,其中A表示的是低秩矩阵,而E表示的是分解后的稀疏误差[4].对传统的低秩矩阵恢复进行一定的优化处理,可对如下公式进行求解,从而使低秩矩阵恢复变得更易于处理:
式中,‖A‖*表示的是矩阵A秩的近似值,为核范数;而一范数‖E‖1代替了原本的零范数‖E‖0.对于这一问题进行求解,其中的关键就在于对于矩阵A的秩的控制.当矩阵A的秩不是很大时,矩阵E也就足够稀疏,此时结合增广拉格朗日乘法,能够提高对低秩矩阵近似问题的求解效率.
而离散余弦变换的应用,能够有效提升人脸识别算法的能量聚焦性,在实际识别图像的过程中,能够将图像从空间域变换到频域当中.此时,绝大多数的图像信号能量,也就被集中在了变换域的少数系数上[5].基于此种技术原理,在进行图像识别时,目标图像受到了光照的影响,在开始识别之前,仅需要修改少量的频域系数,就可以做到调整图像光照的效果,从而降低算法识别过程中,相应的需要调节的参数.
算法当中的人脸重叠分块与识别,其实现过程如下:
1)人脸重叠分块的实现.基于低秩分块稀疏表示的人脸识别算法,其中包含的基于稀疏表示的人脸识别算法认为,每一个目标图片,都是字典当中训练图片集的线性组合.相关稀疏编码问题的解决过程如下:
将测试图片的模块视为字典中Ak的线性组合,则对任意一个测试模块yk都有:yk=Akxk.这种表示方式是一种欠定系统,其目的就是获得一个稳定的、唯一的解.
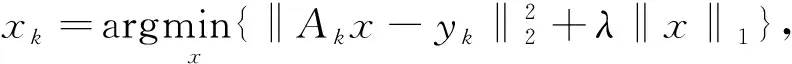
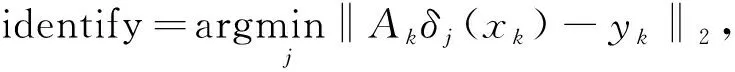
综合对比多种算法的应用效果,在不同像素尺寸下,各个算法的识别率如表2所示.通过对比能够清楚的认识到,对于小图像来说,人脸特征相对较为缺乏,所以模块化的识别方法,要比全局化的识别方法差一些.但上述利用人脸图像当中重叠部分的冗余信息,能够有效提升其识别率.通过对比,能够得出基于低秩分块稀疏表示的人脸识别算法,对于不同像素尺寸的图像,都能实现较高的识别效果.
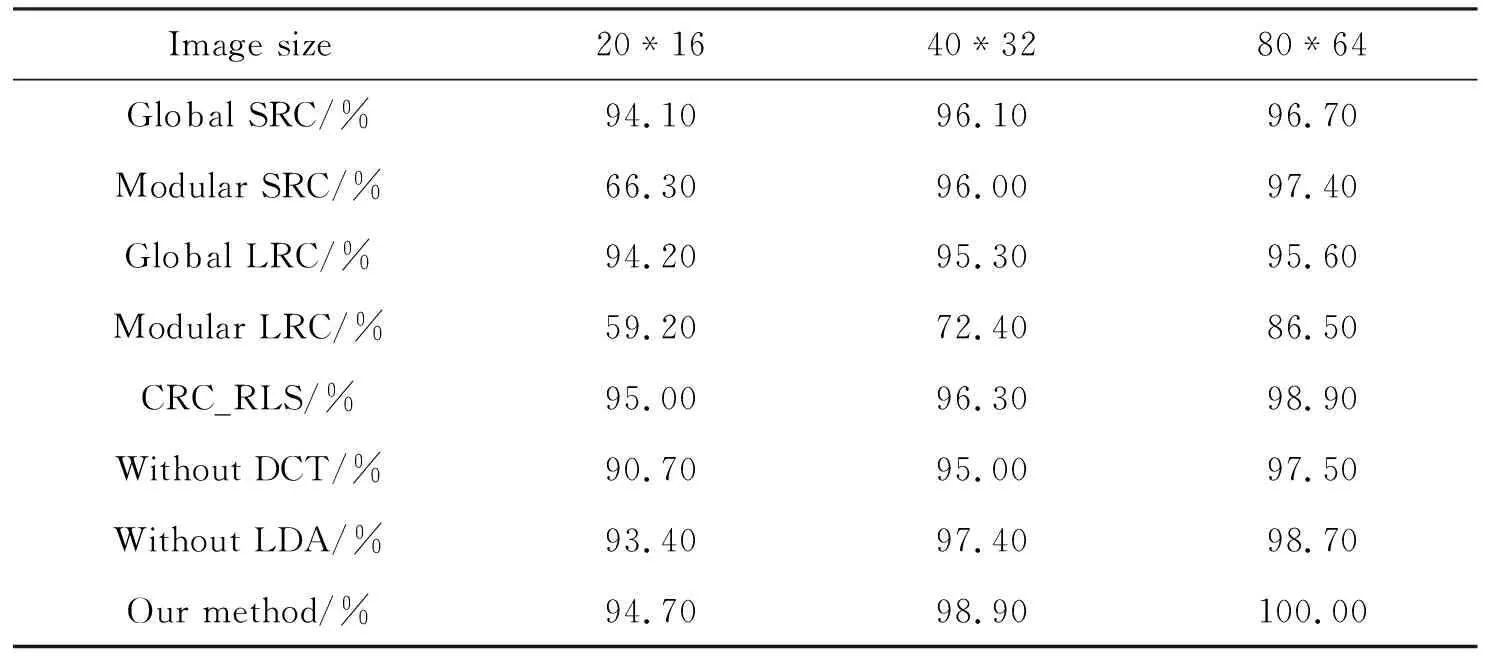
表2 不同像素尺寸下人脸识别算法的识别率
3 人脸识别系统在安防监控中的应用
3.1 人脸识别系统应用在安防监控中的可行性分析
基于图像分块稀疏表示的人脸识别算法作为生物识别领域的尖端技术,将其与安防监控相结合,能够有效解决现阶段视频安防监控中的多种问题,包括无法实时确定监控场景实物、无法锁定监控对象、无法准确识别监控对象、未能实现智能化检索等.从技术的角度分析,基于图像分块稀疏表示的人脸识别算法,能够支撑对大量图像数据的识别与检索,且成功解决了光照、表情变化、遮挡等问题,将其应用于视频安防监控系统当中,能够有效完成对生物特征的提取,以及相关图像信息的比对.
3.2 人脸识别系统在安防监控中的应用实例
以某博物馆为例,该博物馆将人脸识别系统嵌入在视频安防系统当中,重新构建了一个视频人脸预警及检索系统.系统的运行过程中,可以对到馆参观的人员进行全面的、有效的人脸采集;在采集的基础上,若有被识别的参观人员,在30 d内第二次到馆参观,则系统可以自动识别出相关的人脸特征;当同一人员第三次到馆参观时,系统会在预警响应时间内,通过系统管理发布相应的预警信息,同时将参观人员的人脸特征呈现在交互界面上;准确识别预警人员之后,系统还能进一步将其前两次的到馆参观信息通过检索调出,并与公安系统或有关部门的黑名单人员进行综合比对[6].
3.3 人脸识别系统在安防监控中的应用前景
现阶段,人脸识别系统的应用范围包括情报领域、户政管理、种族比对等,除相关以身份识别为核心的生物特征识别市场,随着人脸识别技术水平的不断提升,人脸识别技术逐渐被应用在多种数字产品当中,包括数码相机、手机摄像头等.由此可见,人脸识别技术的应用前景十分广泛,而随着社会背景的变化,其应用将呈现为多样化的发展趋势,包括网络化趋势、融合趋势以及快速发展趋势.以人脸识别系统为媒介,将进一步促进“身份识别+物联网”的认证模式;另外,随着社会对于这一技术的需求标准越来越高,人脸识别系统将逐渐与其他技术进行有机融合,综合提升相关技术应用的整体安全性,提高安防效果.
综上所述,探究基于图像分块稀疏表示的人脸识别算法,对综合提升人脸识别技术水平及应用效果具有重要意义.通过相关分析,基于图像分块稀疏表示的人脸识别算法,对于不可控环境下拍摄的人脸图片的识别效果更好,进一步强化了系统对局部人脸特征的识别作用.这样一来,系统能够更好地应对光照、部分遮挡等对识别效果的影响.
