向量的p-范数及向量序列的收敛性研究

程克玲

(吕梁学院汾阳师范分校 数学与科学系，山西吕梁 032200)

以前我们熟知的实数的绝对值、复数的模、直觉空间中的向量的长度都是范数的概念原型，在内积空间中用内积诱导出的一个范数是一类特殊的范数，它们确实反映了向量长度的几个基本几何性质，即非负性、齐次性以及三角不等式.[1]那么，在一般的线性空间中，也有类似的基本几何性质.

1 向量p-范数的有关定理及证明

定理1[2]对于任意的x=(x1,x2,…,xn)T∈Cn,令

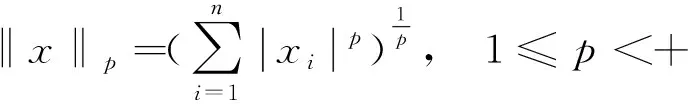
(1)

则‖x‖p是Cn中的一种向量范数，称为p-范数.

要证明向量的p-范数‖x‖p满足向量范数的三个公理，需先证明以下结论：

引理1[3](Young不等式) 设实数p，q均大于1，则∀a,b∈R,有

(2)

证若ab=0,结论显然成立.当ab≠0时，构造函数

(3)

由φ′(τ)=τp-1-τ-(q+1)可知，当0<τ<1时，φ′(τ)≤0;当1≤τ<+时，φ′(τ)≥0,因此φ(τ)≥φ(1)=1,取代入式(2)，有

(4)

因此

结论得证.

(5)

证当xk,yk中至少有一个不为0时，结论显然成立.当xk不全为0，yk也不全为0时，由引理1，有

(6)

于是有

定理3[3](Minkowski不等式) 任取x,y∈Cn,则∀p≥1，有

(7)

证当p=1时，式(7)显然成立.当p>1时，设q为p的共轭指数，于是

(8)

式(8)右端两项各用Holder不等式得

(9)

Holder不等式与Minkowski不等式是泛函分析中的两个基本不等式，在向量的范数中也有其相应的表达形式.它对有限或无限维空间均成立，且有离散及连续两种类型.[4]下面证明定理1.

(1)正定性.显然‖x‖p≥0,而x≠0时至少有一个分量不为0，因此‖x‖p>0.

(2)齐次性.∀k∈C,∀x=(x1,x2,…,xn)T∈Cn,有

(3)三角不等式.由Minkowski不等式，有

于是

‖x+y‖p=‖x‖p+‖y‖p

因此，‖x‖p是Cn中的一种向量p-范数.

2 向量范数的等价性

定义1[5]设V是有限维线性空间，‖x‖α与‖x‖β是V中任意两种范数，若存在正数k1及k2，使得对任意的x∈V,有

k1‖x‖β≤‖x‖α≤k2‖x‖β

(10)

称‖x‖α与‖x‖β等价.

引理2n维向量空间V中的任一向量x的范数都是其坐标的连续函数.

证设V是n维线性空间，e1,…,en为V中的一组基，则对于任意的x∈V有唯一表达式

x=(ξ1e1,…,ξnen)=(e1,…,en)ξ

(11)

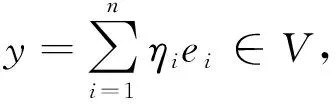
|φ(ξ1,…,ξn)-φ(η1,…,ηn)|= |‖x‖-‖y‖|≤‖x-y‖=

(12)

定理4 有限维线性空间中的任意两种范数都是等价的.

(13)

此为Cn中的一个单位超球面，且S上无零点.

(14)

(15)

其中，ξ为x的坐标向量.

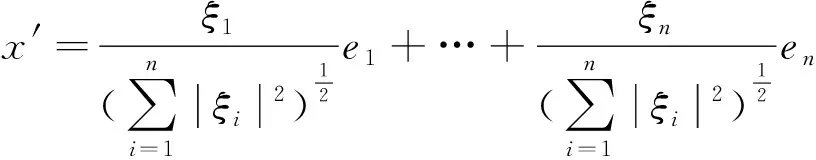
k1‖x‖β≤‖x‖α≤k2‖x‖β

向量范数的等价性在研究向量序列收敛问题时表现出了一致性，即有关按‖•‖α收敛的性质，按‖•‖β也相应成立.

3 向量序列的收敛性

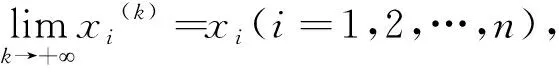
(16)

向量序列不收敛时称为发散的.

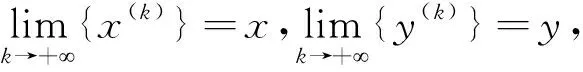
定理6Cn中向量序列{x(k)}收敛于向量x的充分必要条件是，对于Cn上任一向量范数，都有

(17)

证由范数的等价性，只要对‖•‖证明即可.

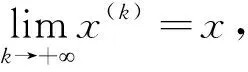
xi(k)-xi→0,i=1,2,…,n

因此

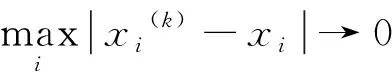
‖x(k)-x‖→0

即

因此

xi(k)-xi→0,i=1,2,…,n,k→+

即

4 结语

本文在一般向量范数概念的基础上，引入了向量的p-范数的概念，并借助Young不等式、Holder不等式和Minkowski不等式对向量p-范数的相关结论给与了证明.本文证明了有限维线性空间中的任意两种范数都是等价的结论，并对向量序列的收敛性进行了探讨.