一类守恒律方程组周期解的存在性
2019-01-10张树兴
张树兴
(南京航空航天大学 理学院数学系,南京 211106)
本文研究如下双曲守恒律方程组
(1)
周期解的存在性,其中ρ,u分别表示密度和速度,κ>0是常数,γ是绝热指数,取值为1<γ<3.该方程组源自于等熵多方气体动力学方程组
(2)
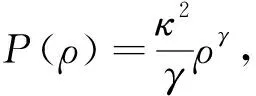
守恒律方程组的周期解一直是许多数学工作者关注的问题,但由于初值的周期性,导致很难利用经典的Glimm格式得到周期解的存在性,但对于一些特殊方程,例如P方程组[1]和方程组(1),其在一定条件下的周期解是存在的.Frid[2]最早对这些方程进行研究,得到了当初值的全变差小于初值的震荡时,P方程组和方程组(1)周期解的存在性.Wang和Zhang[3]通过对近似解更精细的估计,推广了Frid关于P方程组的结论,得到了当初值U0∈L∩BVloc(R)时,存在属于L∩BVloc(R×R+)的周期解U(x,t).本文也是通过对方程组(1)近似解更加精细的估计,得到类似的结果.
对于方程组(1),若引入β满足2β=γ-1,则0<β<1.可求出特征值为
λ1=u-κρβ,λ2=u+κρβ.
令U=(ρ,u),记方程组(1)对应的1-Riemann不变量为w(U),2-Riemann不变量z(U),可求出(见文献[2],[4])
(3)
假设初值U0(x)=(ρ0(x),u0(x))满足
U0(x+L)=U0(x),x∈R
(4)
(5)
TV(U0(x))|[0,L)≜r<
(6)
其中,L为周期,得到的主要结论如下:
定理1 对于方程组(1),假设初值满足(4)~(6),并且满足
(7)
则存在L∩BVloc(R×R+)的全局周期解U(x,t),其周期也为L,并存在某个R>0,使得解满足
z(U(x,t))≤z0,w(U(x,t))≥w0
(8)
TV(U(x,t))|[0,L) (9) (10) 假设初值满足(7),在状态空间中定义一个区域 Ω={U∈R2|w(U)≥w0,z(U)≤z0} (11) 根据Diperna[4]对于方程组(1)的Riemann问题的讨论,可知对任意左右状态Ul,Ur∈Ω,方程组(1)Riemann问题是可解的,并且解全部在Ω内.式(11)表达的区域也被称为方程组(1)的不变区域.在此先假设U关于时间一致有界,即存在不依赖于时间t的常数R>0,使得 (12) 关于R的存在性将由式(20)给出. 首先,将上半平面R×R+网格化,记网格空间和时间步长分别为l=Δx,h=Δt,满足CFL条件: λh≤l,λ=sup{||λi||U∈R,i=1,2}. 另外,取L/l=2N,N为正整数,记tk=kh,定义带状区域: Tk={|(x,t)|(x,t)∈(-,)×[tk,tk+1)},k=0,1,2,… 对初值做分片常数近似: (13) 显然有 (14) 首先用方程组(1),(13)的解来定义在T0内的近似解,该近似解是由众多局部Riemann问题组成的. 为了构造T1中的近似解,随机选取数θ1∈(-1,1),记: Uh(x,h)=Uh((m+1+θ1)l,h-0),ml (15) 在T1内解方程组(1),(15),并把得到的解Uh(x,t)定义为在T1的近似解. 随后依次在Tk(k=2,3,…,)内构造近似解,在构造过程中,选取随机数列θk∈(-1,1)来定义在时刻tk处的分片常数Uh(x,tk): Uh(x,h)=Uh((m+1+θk)l,h-0),ml (16) 这样就得到了原周期Cauchy问题的在上半平面的近似解. 由w,z的表达式(3),可得 (17) d(U1,U2)=(σ(U1)-σ(U12))++(σ(U12)-σ(U2))+ (18) 下标的加号表示正部.需要注意的是,(18)式只记录了σ的减变差,由上面的分析,即只记录激波强度. 对于任意含第一类间断点的函数f(x),可以定义间断点的跃度[f]=f(x-)-f(x+),对于激波而言,激波两侧的状态U的跃度[U]也可以作为激波的强度的一种表示. 命题1 记DV(w(Uh(t))),DV(z(Uh(t)))为w(Uh(t)),z(Uh(t))的减变差,则有 证明由于只有越过激波,w(Uh(t)),z(Uh(t))才可能减小.当U1和U12以1激波相连,则有w(U1) DV(w(Uh(t)))+DV(z(Uh(t)))=z(U1)-z(U12)≤ (z(U1)-z(U12))+(w(U12)-w(U1))= η(U12)-η(U1)= |[η(U)]|. 当U12和U2以S2相连时,可相似的得到. 引理1[4]若U1,U2,U3∈Ω,则 d(U1,U2)≤d(U1,U3)+d(U3,U2). 另外,如果U3是以U1为左状态,U2为右状态的Riemann问题解中出现的状态,则有 d(U1,U2)=d(U1,U3)+d(U3,U2). 对函数U=(ρ(x),u(x))∈BVloc(R,R+×R),定义 其中,最大值是取遍[a,b]中任意满足a=x0 Fper(Uh(t))=μh,t([a,a+L)), 这里μh,t是指由Glimm格式得到的近似解Uh(x,t)所定义的测度,a∈R是任意的. 命题2Fper(Uh(t))的周期为L,同时不依赖于a,即对任意的a∈R,有 μh,t([a,a+L))=μh,t([0,L)). 证明由Uh(t)的周期性和Fper(Uh(t))的定义,上述结论是显然的. 命题3Fper(Uh(t))关于t是不增的,特别地,有 Fper(Uh(t))≤Fper(Uh(0)) (19) 于是得到Fper(Uh(t))关于t是不增的,并得到式(19). 命题4 近似解在一个周期内的全变差TV(Uh(x,t))|[0,L)关于t>0一致有界. 证明当方程组(1)近似解有界时,Uh(x,t)在一个周期内的全变差可以与对应的Riemann不变量在一个周期内的全变差相互控制(见文献[2],[3]),由命题1、命题3和引理2可得: TV(Uh(t))|[0,L)≤C1(TV(w(Uh(t)))|[0,L)+TV(z(Uh(t)))|[0,L))= 2C1(DV(w(Uh(t)))|[0,L)+DV(z(Uh(t)))|[0,L))≤ 其中,C1,C2依赖于近似解的界. 由于初值满足(6),记 (20) 接下来,将证明近似解的有界性.在此之前,先给如下关于周期解的一个引理: 引理3[3]对任意t>0,方程组(1)的周期解序列{Uh(x,t)}的一个子列,这里依然记为{Uh(x,t)},满足 (21) 引理3表明,对任意t>0时刻,在一个周期上的解的平均值保持不变. 命题5 近似解Uh(x,t),对任意的t>0,有 (22) R+A(h) 在证明周期解的存在性之前,先给出近似解Uh(x,t)的L1范数关于t的一致性: 引理4[5-7]近似解Uh(x,t)对任意的t1,t2>0满足 其中,C只依赖于R和r. 到此,我们得到了所有可能用到的结论,由于命题4,命题5和引理4,由Glimm格式框架[8],得到近似解Uh(x,t)中存在子列Uhs(x,t)收敛到方程弱解U(x,t),同时由命题4得到式(9),由命题5得到式(10). 本文利用改进的Glimm格式,研究守恒律方程组(1)带有周期初值条件的解的整体存在性,该方程来源于等熵的多方气体动力学方程.利用Riemann不变量的和σ定义波的强度,得到了对近似解全变差的估计,随后利用周期解在一个周期内平均值保持不变的性质,证明了近似解的有界性,最后利用Glimm格式的框架得到了周期解的存在性.
1 用Glimm格式构造的近似解

2 近似解的全变差和有界性估计
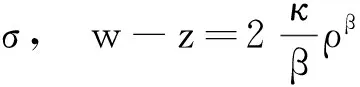

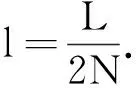
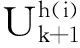
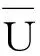
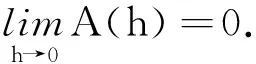
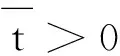
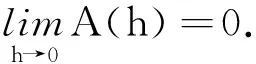
3 周期解的存在性
4 结语
