某发动机用自动张紧器张紧臂断裂原因分析及改进优化

于超，曾超，程市，王景新

（内燃机可靠性国家重点实验室，山东省潍坊市261061；潍柴动力股份有限公司，山东省潍坊市261061）

0 引言

多楔带传动已被广泛应用于发动机行业[1]。因其为弹性体，运转过程中受拉伸而变长，初始张紧力减小，而自动张紧器可维持合适的皮带张紧力，所以能保证传动系统工作正常。就机械传动系统而言，其可靠性是指系统中所有零部件在规定的试验载荷冲击和振动下，完成耐久考核试验的能力[2]。

文献 [3-8]根据市场故障及轮系特性分析了发动机前端轮系 （_Front End Accessory Drive System，FEADS）某些零部件及系统的性能。这些零部件和系统通过优化均能得到良好的改进效果，这在一定程度上为前端轮系可靠性提供了保障。本优化项目亦是因市场反馈故障，经分析得出了故障原因，而提出不同的改进优化方案，然后进行验证，并根据机械传动系统可靠性，最终确定了改进优化方案，为设计方向提供了参考。

1 问题描述及初步分析

市场反馈，在整车道路试验时，某新开发的发动机前端轮系中，外协件自动张紧器张紧臂断裂。返回的故障自动张紧器如图1所示。

图1 故障件

在设计时，张紧臂采用压铸铝合金材料。经质检分析，断口为疲劳裂纹扩展所致，原因极有可能为张紧臂受交变应力，薄弱处出现裂纹，最终扩展而发生断裂。借助有限元分析方法加以佐证，并提出相应的改进优化方案。

2 问题的有限元分析

2.1 发动机前端轮系模型

根据发动机前端轮系布置，除惰轮、自动张紧器外，轮系主要由曲轴皮带轮驱动风扇、水泵、发电机1、发电机2等附件。采用Simdrive 3D仿真分析软件建立发动机前端轮系模型，如图2所示。

图2 发动机前端轮系计算模型

2.2 有限元分析边界条件

2.2.1 几何边界条件及转动惯量

根据发动机前端轮系布置，确定发动机前端轮系几何边界条件及转动惯量参数，如表1所示。

2.2.2 张紧器受力分析

对于直列4缸发动机，主激励谐次下的曲轴系扭转振动特性曲线如图3所示。

发动机前端轮系中，2个发电机的速比、性能均相同。2个发电机、风扇及水泵附件，在不同发动机转速下的功率消耗曲线如图4所示。

发动机前端轮系采用自动张紧器及聚酯线绳EPDM（三元乙丙橡胶）多楔带。在扭转检测台上测得自动张紧器 （名义位置为20°）的扭转特性曲线，如图5所示。

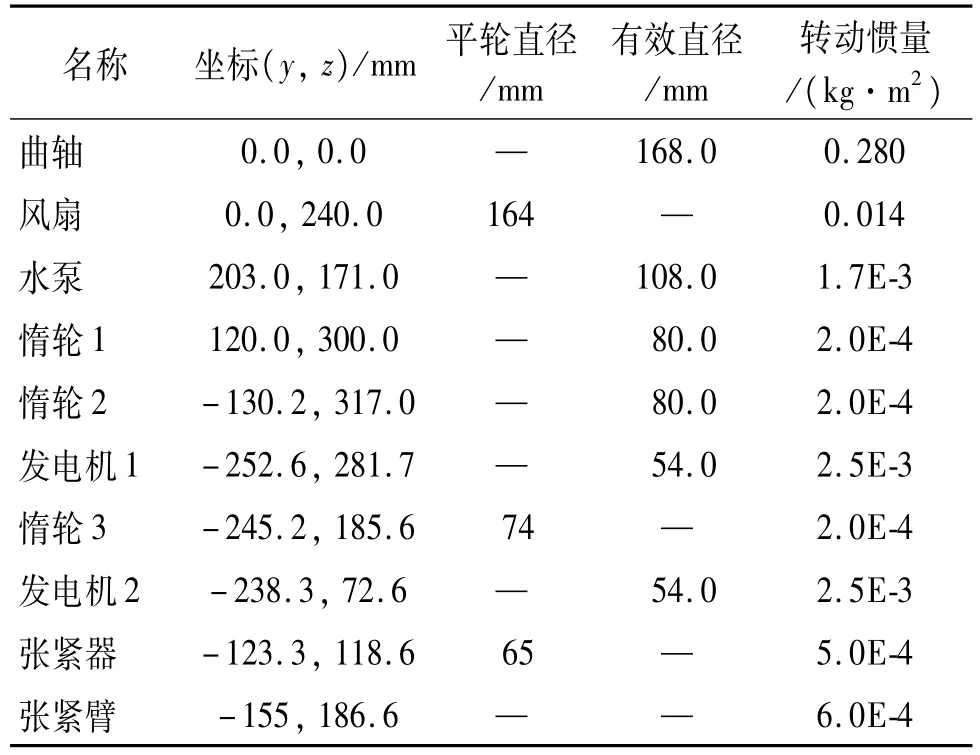
表1 发动机前端轮系几何边界条件及参数

图3 曲轴系扭转振动特性曲线

由发动机前端轮系模型，计算得从怠速至最高空车转速下自动张紧器的张紧轮所受的最大合力情况，并作为有限元分析的边界条件，间隔50 r/min进行取值。张紧轮所受合力大小及角度 （合力角度为受力方向与垂直向上方向的夹角）如图6所示。

图4 发动机附件功率消耗曲线

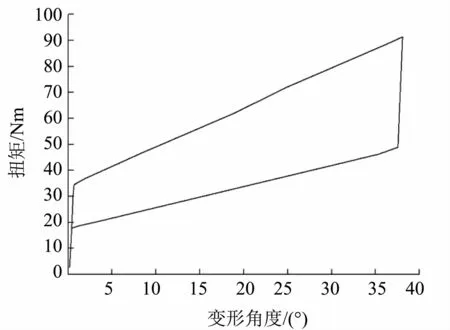
图5 自动张紧器扭转特性曲线

图6 张紧轮受合力大小及角度

2.3 有限元分析

根据自动张紧器工作原理及受力特点，仅对张紧臂及自动张紧器轴螺栓进行简化分析，采用2阶C3D10I网格单元，细化断裂区域，建立有限元模型，如图7所示。

张紧轮合力作用点施加在轴螺栓中部。张紧臂采用压铸铝YL112，弹性模量为71 000 MPa，泊松比为 0.33，密度为 2 760 kg/m3，轴螺栓采用40Cr，弹性模量为205 000 MPa，泊松比为0.29，密度为7 850 kg/m3。

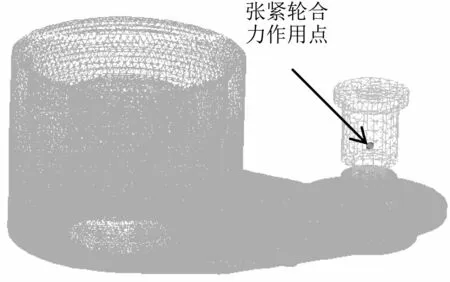
图7 有限元模型

在有限元分析软件Abaqus中，输入载荷条件（见图6），分析不同转速下张紧臂的应力值。从分析结果中可以看出，2 000 r/min时，张紧臂应力最大，为181.7 MPa，超出所应用材料的屈服极限159 MPa。2 000 r/min时张紧臂的应力分布如图8所示。

图8 张紧臂应力分布

由Abaqus软件分析得到应力值，在FEMFAT软件中，利用TransMAX模块对张紧臂进行疲劳分析，所得高周疲劳安全系数结果如图9所示。

图9 张紧臂高周疲劳安全系数分布

从图8和图9可以看出，张紧臂在四方安装孔处应力值超限。此处在不同转速下受冲击载荷时，应力变化较大，导致张紧臂疲劳安全系数较低。由此可佐证断裂为疲劳所致。

3 问题的理论分析及自动张紧器通程化方程的建立

3.1 理论分析

主动轮和从动轮均会将因旋转离心力及自身转动惯量参数引起的扰动力传入传动装置，使得系统中带轮转速并非为恒定值。系统运转过程中，自动张紧器张紧臂的往复摆动，内部弹性元件的扩张或收缩，以调节自动张紧器的张紧轮实时压紧多楔带，保持系统中合适的皮带张紧力，保证传动系统正常工作，也使自动张紧器的张紧轮所受的合力为非恒定值。变化着的合力作用于张紧轮，而张紧轮通过轴承、轴螺栓等与张紧臂连接，使张紧臂不断产生拉伸和压缩的交变应力，工作一段时间后，薄弱处产生裂纹，最终导致张紧臂疲劳断裂。

自动张紧器的往复摆动对轮系的性能有很大影响，为保障发动机前端轮系的可靠性，需对自动张紧器的受力特性进行分析。

3.2 自动张紧器通程化方程的建立

建立自动张紧器的通程化运动方程[9]，可分析自动张紧器的受力特性。某工作时刻，自动张紧器的受力情况如图10所示。

图10 自动张紧器受力示意图

自动张紧器主要承受自身弹性元件和阻尼元件产生的力矩、惯性力矩、张紧轮重力矩及初始预载力矩，以及外部皮带拉力产生的力矩及相邻皮带轮的惯性力矩。根据动量矩守恒定律，建立自动张紧器的运动微分方程：

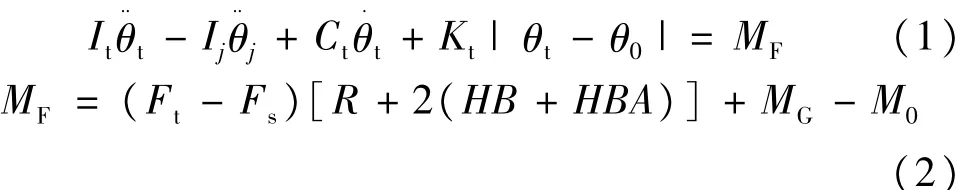
式中，It为张紧臂转动惯量，kg·m2；Ij为附件及对应带轮转动惯量 （j为附件带轮编号，从曲轴皮带轮逆时针开始计数， j=1，2，3， …）， kg·m2；Ct为自动张紧器阻尼刚度，Nm·s/rad；Kt为自动张紧器弹簧刚度Nm/rad，；θt为张紧臂转角，rad；θ0为张紧臂初始转角，rad；MF为合力扭矩，Nm；Ft为自动张紧器紧边拉力，N；Fs为自动张紧器松边拉力，N；R为张紧轮半径，m；HB为多楔带背面到中性层的距离，m；HBA为有效线差，m；MG为重力矩Nm，单位；M0为自动张紧器预载扭矩，Nm。

通过公式 （1）和公式 （2）可以看出，减小张紧臂转动惯量，可抑制紧边拉力与松边拉力之差，使得自动张紧器的张紧轮受力较均匀，从而减小了张紧臂的拉伸及压缩应力幅，提升张紧臂的疲劳安全系数。

4 结构优化

4.1 优化方案

原始结构最大应力超出屈服极限，最大应力出现区域主要在四方孔处。通过3维结构模型及实际铸造模型 （图1）可以看出，此处倒圆角半径偏小，仅为0.5 mm，存在明显的应力集中，故增大此处倒角，以平缓此过渡区域，从而可明显降低应力集中，使张紧臂应力满足设计要求。综合张紧臂高周疲劳安全系数分布情况分析可知，仅增大过渡处倒角，一定程度上可提升张紧臂安全系数，但效果有限。

自动张紧器为外协件。供应商根据张紧臂故障分析结果，及与原始结构相同臂长，且安装孔径相同的自动张紧器的要求，提供了3种张紧臂结构优化的自动张紧器方案，如图11所示。

图11 3种张紧臂结构优化的自动张紧器方案

从图11中可以看出，3种方案中，四方孔处结构强度均有所加强，主要区别在于方案1将四方孔移至张紧轮背面处，方案2将四方孔布置于张紧轮一侧封闭，方案3为保留四方孔，将其移动至张紧臂外侧边缘。

鉴于整车发动机机舱中，发动机前端轮系安装空间有限，结构布局要求日渐严苛，决定采用方案1或方案2。首先考查方案1和方案2的结构可靠性，若不能满足要求，则在各自基础上进行适度更改。

4.2 方案验证

采用2.3节相同分析方法，分别计算方案1和方案2自动张紧器的应力分布情况。计算结果如图12所示。

图12 改进结构应力分布

从图12中可以看出，2 000 r/min时，方案1张紧器的张紧臂应力最大值为55.4 MPa，方案2的张紧臂应力最大值为58.9 MPa，均低于所应用材料YL112的屈服极限159 MPa，结构强度满足设计要求。

同样，对2种方案张紧器的张紧臂进行疲劳分析，所得高周疲劳安全系数结果如图13所示。

从图13中可以看出，方案1和方案2张紧器的张紧臂疲劳安全系数均大于1，风险性较低，从结构可靠性而言，2种方案的结构均满足设计要求。

另据公式1～2可知，减小张紧臂自身转动惯量，可有效降低紧边拉力与松边拉力的力矩和，降低张紧轮合力，从而减小张紧臂的交变应力幅值，提升高周疲劳安全系数。

根据3维模型，以张紧臂与安装基座中心点为原点建立笛卡尔坐标系，指向张紧轮中心为x轴，垂直上向为z轴，根据x轴和z轴确定y轴，如图14所示。

图13 改进结构高周疲劳安全系数分布

图14 建立的笛卡尔坐标系

测得方案1张紧器的张紧臂绕z轴的转动惯量，为7.08×10-4kg·m2；方案2的张紧臂绕z轴的转动惯量，为7.48×10-4kg·m2。因此，综合考虑张紧器结构可靠性、发动机前端轮系可靠性等因素，最终决定采用方案1张紧器。

对方案1张紧器，进行道路试验及耐久考核试验。直至试验结束，未复发张紧臂断裂情况，轮系动态性能亦满足设计要求，验证了方案1结构改进的合理性，有效确保了机械传动系统的可靠性。

5 结论

目前整机零部件由众多供应厂商分别供货，单个零部件可靠性极有可能是机械传动系统可靠性的掣肘，影响客户满意度。对道路试验中暴露出的张紧臂断裂故障情况，从张紧臂的材料及结构进行分析，并借助于有限元计算，佐证了故障原因分析。综合考虑张紧臂的结构可靠性及其对发动机前端轮系可靠性的影响，提出几种不同的结构方案，并采用有限元方法进行对比分析。分析结果表明，在结构可靠性均满足设计要求的前提下，优先选用转动惯量小的张紧臂，对轮系系统可靠性更优，更能提升机械传动系统的可靠性。