计及DG随机性的配网无功优化与降损策略

王冠翔 ，郭文萍 ，廖敬丹 ，陈国发 ，张永年

（1.国网甘肃省电力公司武威供电公司，武威733000；2.兰州理工大学 电气工程与信息工程学院，兰州730050）

在全球能源危机背景下，世界各国都在开展节能减排和发展可再生能源技术，减小网损是缓解能源危机和实现节能减排的重要手段[1]。由于我国配网尤其是农网存在网架结构薄弱、无功补偿设备老化等问题，导致损耗严重，因此研究降低配网损耗的措施尤为重要。配网损耗包括两个方面，即设备损耗和系统运行损耗。采用先进的优化方法，对配电网进行无功优化，是降低电网损耗十分重要和有效的手段。通过合理配置接入配电网中的DG，不仅可以减小系统网损，提高电能质量，还可以提高配电网经济效益。但DG在电网中的渗透率不断提高，改变了电网原先潮流分布、配电网形态和结构，使得配电网变得更复杂，协调运行更困难，尤其是DG出力的随机性和柔性负荷的实时变化都会对配电网的优化结果产生较大影响。传统的无功优化把DG的出力等价为一个恒定功率输出的PQ型电源，忽略了分布式电源本身所具有的随机性，不能很好模拟DG间歇性对配电网的影响，因此传统无功优化策略不再适用[2]。

目前，针对含DG配电网无功优化问题中，DG和负荷的不确定性及波动性问题，国内外学者展开了大量的工作。文献[3]将转换侧电流作为限制条件，利用概率论方法分析了风电机组的输出特性，建立不同场景下含风电机组的配电网无功优化模型，并采用融合了微分进化的细菌群体趋药性算法，对模型进行求解。文献[4]针对风机出力的随机性，提出基于拉丁超立方采样的Monte Carlo概率潮流计算方法CLMCS（correlation Latin hypercube sampling Monte Carlosimulation），形成风速场景，采用场景缩减技术，得到风机出力的典型场景，将不确定性问题转化为确定性潮流问题。但以上参考文献仅考虑了配电网无功优化中风电机组的随机性问题，但在实际的电网运行中，光伏发电出力与负荷的随机性同样会对含DG配电网的无功优化带来影响。

此外，传统配电网无功优化大多以网损最小为目标函数建立数学模型，忽略了电网的电能质量。为此，本文在现有文献的基础上，考虑电网的电能质量与经济效益，建立了以有功网损、电压偏差最小为多目标函数的数学模型。提出一种基于高斯变异和混沌扰动的人工蜂群算法，求取目标函数最优解。该算法在传统ABC算法的基础上，引入高斯变异，加强了局部搜索能力，搜索精度更高。加入混沌扰动克服了个体易陷入局部最优的不足，同时提高了算法的鲁棒性。最后，在改进的IEEE-33节点配电网系统中，验证了所提方法的有效性。

1 基于最优场景法多目标优化模型

1.1 Wasserstein距离指标

为了准确实现含DG配电网的无功优化，就不能忽略配电网中DG和负荷的随机性，所以考虑通过场景法得到DG真实出力的近似值。

Wasserstein概率距离[5]定义为两个概率分布之间的距离，记作 dw，r：

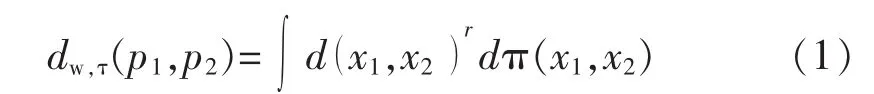
式中：p1和 p2为概率密度函数；π（x1，x2）为联合概率密度函数；r为阶数。因此，保证dw，τ最小，以将离散概率分布，近似转化为连续分布的近似问题。

根据场景模拟的思想，为获得最优场景，即使得 Wasserstein 距离 dr（p，）最小，则需要求解概率测度函数的最优分位点zs及对应的概率，其中=上的点质量。

Wasserstein距离指标下的最优分位点zs由下式表示为

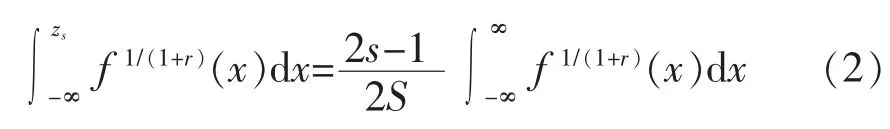
式中：x为一维连续变量，f（x）为x的概率密度函数，S为离散分位点的个数。

分位点zs的概率ps表示为

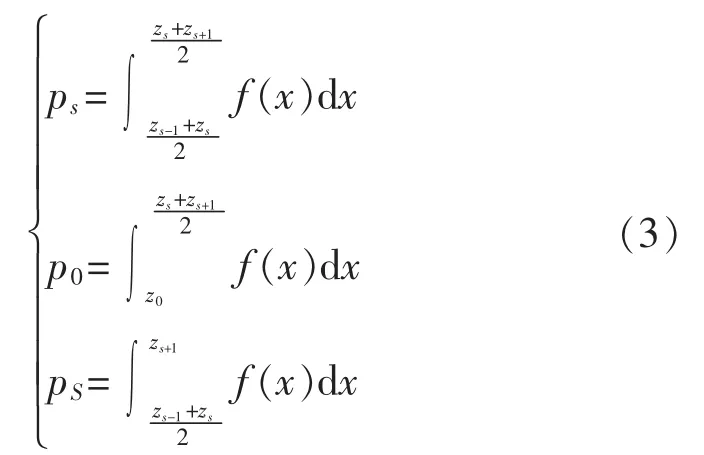
式中：z0=-∞；zs=+∞；s=2，…，S-1

1.2 基于Wasserstein距离的多场景模型

1.2.1 风电机组输出的最优分位点

风机出力概率密度函数为

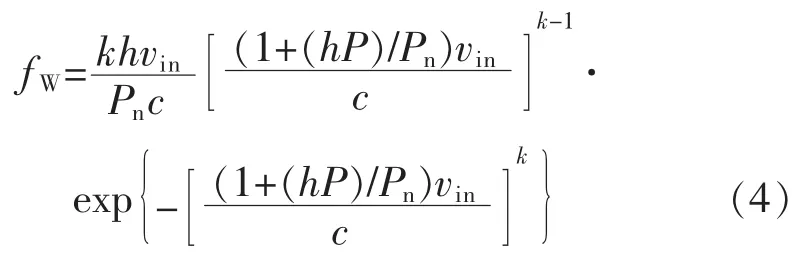
其中：

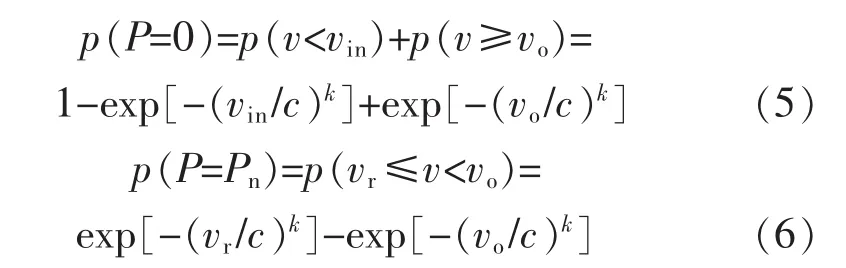
式中：P为风力机组的输出功率；vin为切入风速；vr为额定风速；vo为切出风速；h=（vr/vin）-1；Pn为风电机组的额定功率；c＞0为概率分布的尺度参数；k＞0为形状系数。

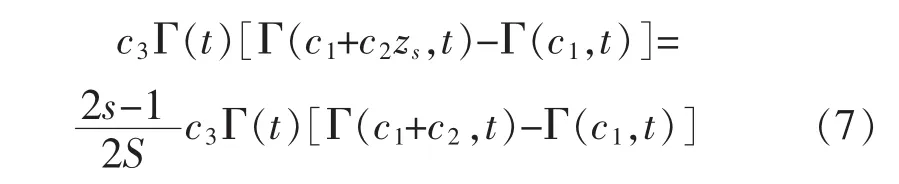
式中：t=（k+r）/［（1+r）k］ 且一般取 r=2，c1=vin/c，c2=（vin/c）/（h/pn），c3=（kc2）-r/（1+r）（1+r）t。

1.2.2 光伏输出的最优分位点

光伏出力概率密度函数：

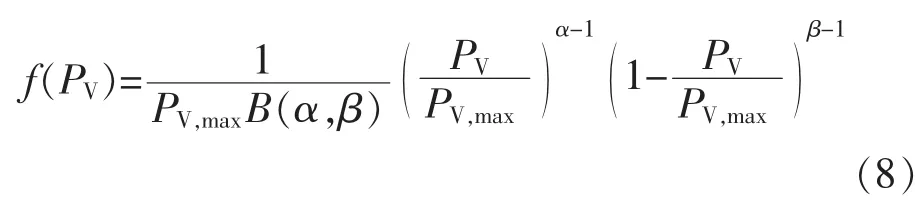
式中：PV，max为最大光伏功率；B（α，β）为 Beta 函数；α、β为Beta分布的形状参数。

将式（8）代入式（2），得光伏出力离散分位点：

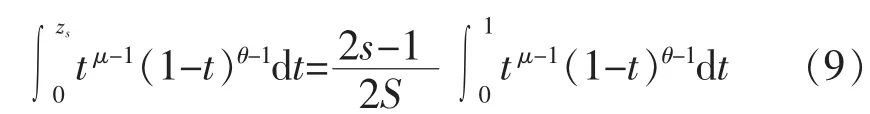
1.2.3 负荷模型

同一地区的负荷因为昼夜与季节等因素，导致随机性和波动性较强，因此把负荷作为一个随机变量来考虑，依据以前负荷状态，对负荷进行预测，采用离散分布近似连续分布。根据负荷预测曲线，将负荷划分为nd个不同的运行状态，对应概率为pndd。

1.2.4 多场景模拟

风电、光伏出力和负荷的场景集合δSC，由式（10）表示为[8]

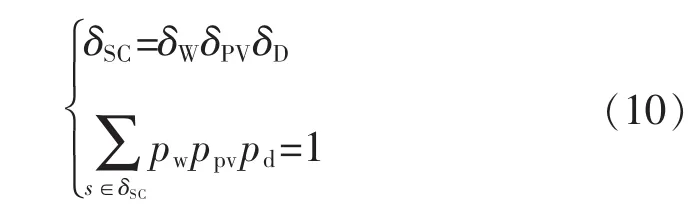
式中：δW、δPV和 δD分别为风电、光伏出力和负荷的离散概率分布集合；pw、ppv和pd分别为风电、光伏出力和负荷在不确定情况下的概率。系统在场景s下的概率：

1.3 目标函数

传统电力系统配电网无功优化，数学模型多以有功网损最小为目标函数，忽略了电网电能质量，因此本文在网损的基础上考虑了电压偏差。

1.3.1 多目标优化模型

（1）有功网损最小

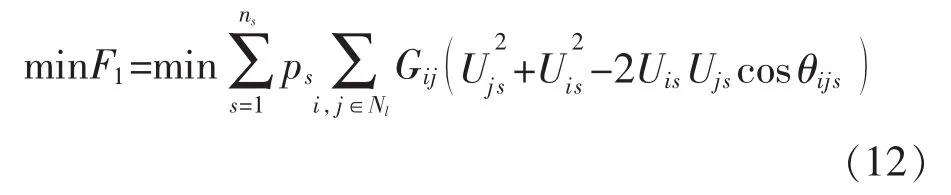
式中：F1为系统有功网损；s表示第s个场景；Gijs为节点i、j之间的电导；θijs为节点i、j之间的电压相角差；Uis、Ujs分别为节点 i、j的电压幅值；Nl为网络输电线路集合；ns为场景数。

（2）电压偏差最小

式中：F2为节点电压偏差；Ui*s为节点i的额定电压；Uimax、Uimin为节点i的最大、最小允许电压；NL为系统负荷总节点数。

1.3.2 约束条件

（1）等式约束条件

式（14）为配电网运行的潮流方程：

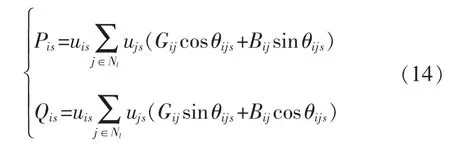
式中：Pis、Qis为节点i注入的有功功率与无功功率；Ni为所有与节点i相连的节点集；Bij为节点i、j之间的电纳。

（2）不等式约束条件

节点电压约束：

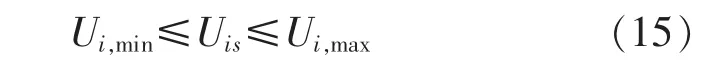
DG输出有功功率约束：

无功补偿容量约束：

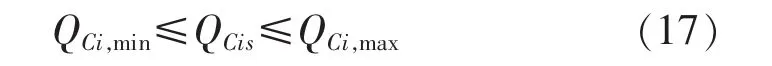
电容器组数约束：

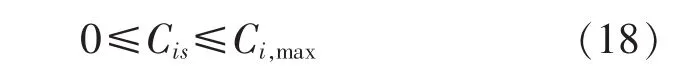
变压器分接头档位约束：

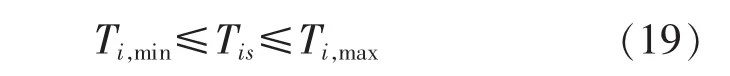
支路传输功率约束：

2 基于改进人工蜂群算法的模型求解

2.1 传统人工蜂群算法

Karaboga在2005年，提出了ABC算法及相关改进算法。将ABC算法应用于实际的工程优化问题。通过与其它智能群优化算法，例如粒子群算法PSO（particle swarm optimization）、遗传算法 GA（genetic algorithm），进行性能比较，指出ABC算法更适合处理工程中的高维优化问题。

ABC算法描述如下，问题中的各种可能解由算法中的蜜源表示，在寻优的过程中，解的优劣性用适应度函数值的大小表示。引入三种蜂：采蜜蜂，观察蜂，侦查蜂。采蜜蜂与所求问题的具体解联系在一起，在求取最优解的过程中通过与其他蜜蜂交换信息来接近最优解，观察蜂则通过分享采蜜蜂的信息对所求解做出选择，侦查蜂随机搜索新位置[7]。

在寻优的过程中，解的质量和选择概率采用式（21）计算，由观察蜂做选择：

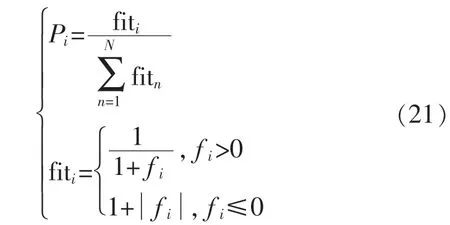
式中：fiti为第i个解所对应的适应度函数值；N为解的数量，等于采蜜蜂的数目。

ABC模型通过式（22）从已求得解对应的个体位置中随机产生一个新解，即：

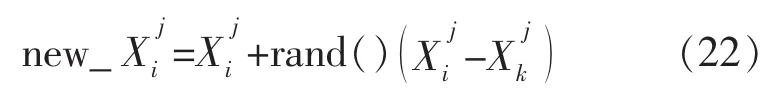
式中：i，k∈｛1，2，…，N｝与 j∈｛1，2，…，D｝是随机选取的，但k不等于i；D是优化问题参量个数；rand（）取值范围为［-1，1］，控制蜜源位置 Xij周围的产量。每个新解new_Xij产生后，该解与Xij进行比较。如果产生的新解所对应的适应度函数值，比旧解所对应的适应度函数值大，则用产生的新解替代原来解；否则，保持原来解不变。

传统ABC算法作为一种新的工程优化算法，相比于其他优化算法，虽然在很大程度上增加了找到问题最优解的概率，但是在寻优过程中，算法依然存在各种缺点，例如容易过早收敛、个体易陷入局部最优等。为了避免出现上述问题，本文采用改进的高斯变异和混沌扰动的人工蜂群算法，在加强局部搜索能力，避免过早收敛的同时，对导致算法停滞的个体，采用混沌序列对其进行扰动，以跳出局部最优。

2.2 改进的ABC算法

2.2.1 高斯变异

高斯变异描述如下，用符合均值为μ，方差为σ2的正态分布的随机数来替代原本参数值[8]。变异公式由式（23）表示：

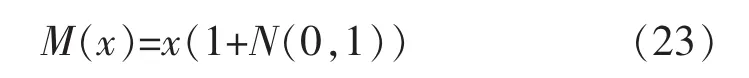
式中：x为原有解；N（0，1）为符合正态分布，期望为0，标准差为1的随机数；M（x）为经过高斯变异之后的数。

对于工程优化过程中的局部极小值问题，采用高斯变异，可以提高算法的局部搜索能力，能够在快速、准确找到全局极小点的同时增强算法的鲁棒性。

2.2.2 混沌搜索

混沌是一种具有随机性的运动状态，由确定的方程通过添加扰动变量得到。传统ABC算法在求取最优解过程中，如果某个解经过多次迭代之后，其所对应的适应度函数值仍然偏小，则表明对应个体陷入局部最优，而混沌扰动则可以利用混沌变量自身的遍历性与随机性，以该解为基础随机产生混沌序列，用此混沌序列对部分导致搜索停滞也即陷入局部最优的个体采取一定扰动，以促使算法跳出限制继续搜索[9]。

考虑Tent映射的值较为平缓，所以选择Tent映射来产生混沌序列。Tent映射公式为

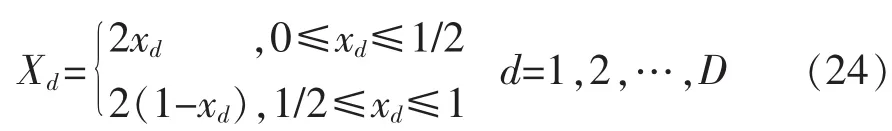
式中：Xd为混沌序列X的第d维向量；xd为一个服从均匀分布的随机数，xd∈［0，1］。

混沌扰动的步骤描述如下[10]：

（1）应用Tent映射产生的混沌变量；

（2）按照式（25）将混沌变量映射回优化问题的解空间：

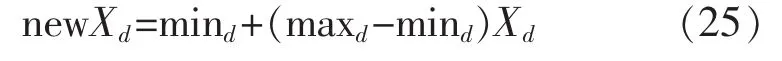
式中：maxd和mind分别为d维向量newXd的最大、最小值；

（3）按照式（18）对个体进行混沌扰动：

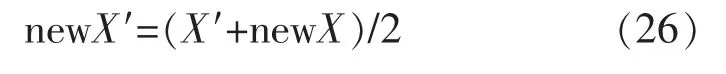
式中：X′为陷入局部最优的个体；newX为随机产生的混沌扰动量；newX′为扰动后的个体。

2.3 算法应用

（1）初始化，设置配电网参数、蜂群大小等；

（2）随机产生初始解，计算个体适应度值，记录当前最优解；

（3）按式（22）寻找新解，对比选择最优解，其对应的个体位置；

（4）如果寻找新蜜源的次数达到最大值Limit时，还没有找到更优的解，则随机产生一个解替代之前解；

（5）计算蜂群中个体的适应度值与平均适应度值，个体适应度大于平均适应度，按式（23）计算，否则按式（26）进行计算，如果变异/扰动后性能更优，则代替之前个体，否则保持原个体不变；

（6）迭代达到最大次数后输出最后结果，否则返回步骤（3）继续执行。

无功优化算法求解流程如图1所示。

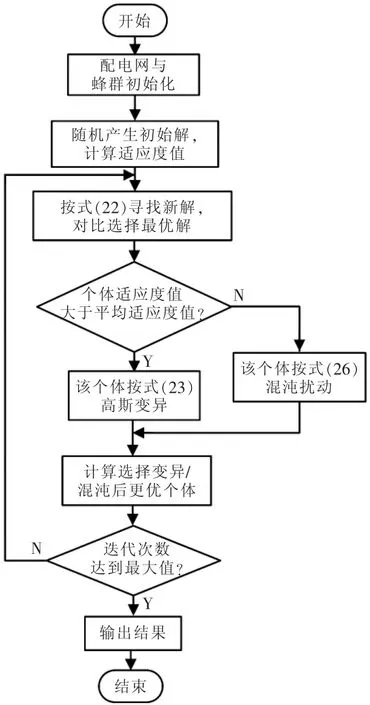
图1 无功优化算法求解流程Fig.1 Reactive power optimization algorithm solution flow chart

3 算例分析

本文采用如图2所示的IEEE-33节点系统进行分析，该系统的电压等级为12.6 kV，总负荷为3715 kW和2300 kvar，原始网络数据参数参见文献[11]。为验证本文所提方法，对该系统做如下修改。在节点6、节点13、节点30各安装20组电容器，每组容量50 kvar；在节点10、节点20接风电机组，所有机组参数设置相同；在节点16、节点24接光伏发电系统，所有DG额定容量均为800 kW，功率因数为0.95；有载调压变压器额定容量为50 MVA，档位调节范围为0.9～1.1，分为9档；节点电压上下限允许范围为0.9～1.1。风电机组和光伏发电机组参数如表1和2所示。

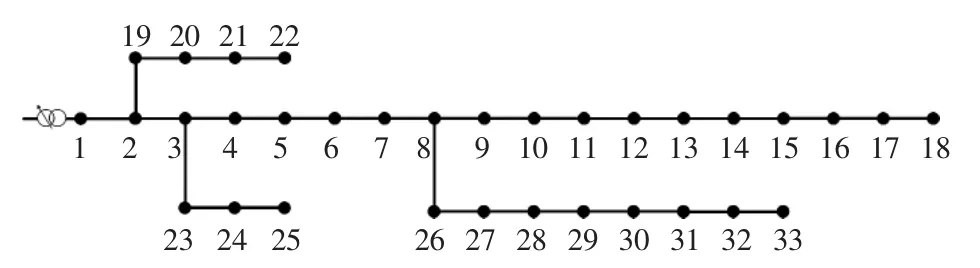
图2 IEEE 33节点系统结构Fig.2 IEEE 33-node system structure

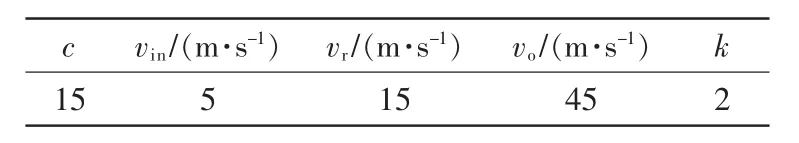
表1 风电机组参数Tab.1 Wind turbine parameters

表2 光伏发电参数Tab.2 Photovoltaic power generation parameters

为了实现DG接入配电网后的安全稳定运行，需要准确掌握DG出力的变化情况，精确预测发生的各场景。图3为风电机组和光伏发电，典型日出力曲线，与采用Wasserstein距离法得到的随机场景曲线对比图。从图中可以看出，本文所提的最优场景法能够全面反映风机和光伏出力的随机性。图中P为风电、光伏机组的实际功率，Pn为风电、光伏机组的额定功率。

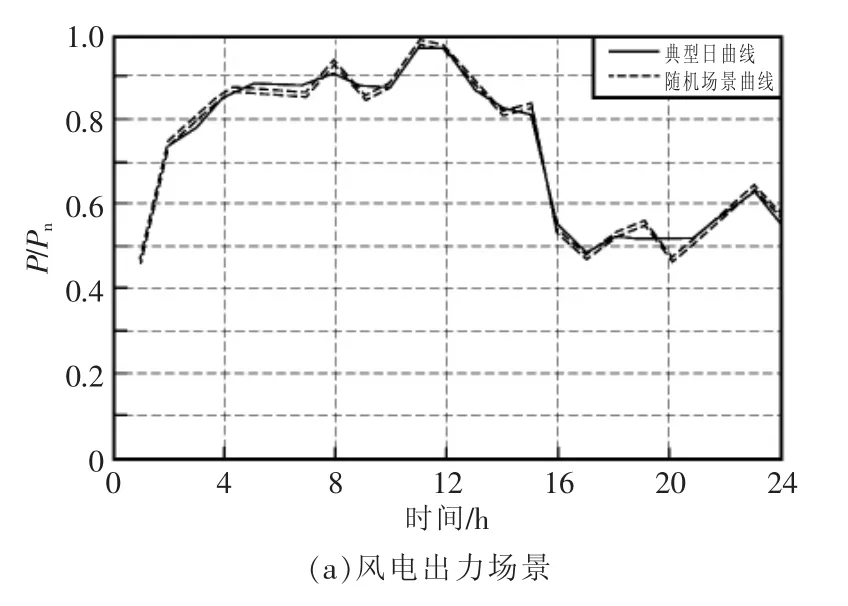
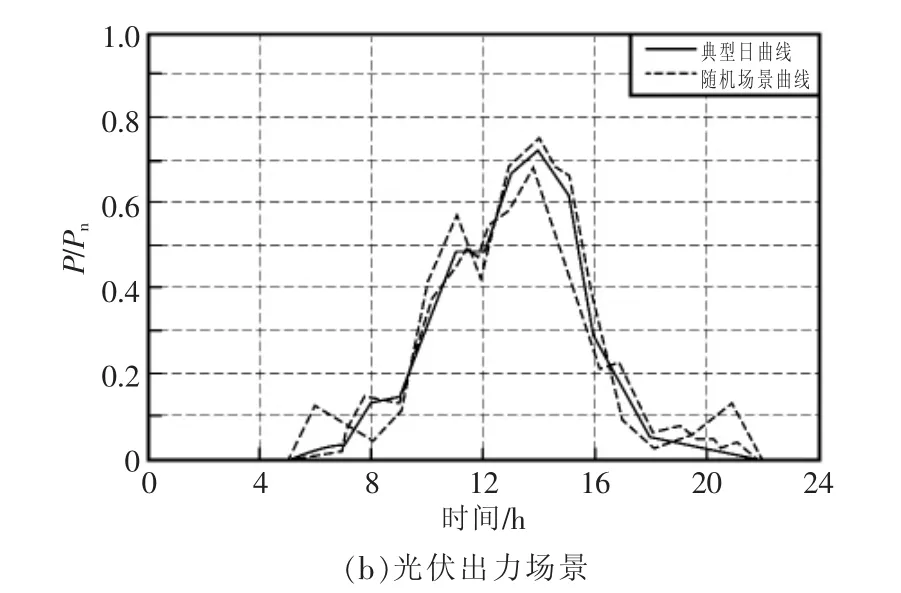
图3 风电和光伏出力场景Fig.3 Scenario wind power and PV power output

图4为GA、传统ABC和改进ABC算法寻优的对比收敛曲线。从图中可以看出，改进ABC算法，相比其他两种算法收敛速度更快，精度更高，优化效果更好。因此，应用改进ABC算法求取全局最优解，能够有效减小含DG配电网的有功网损与电压偏差。

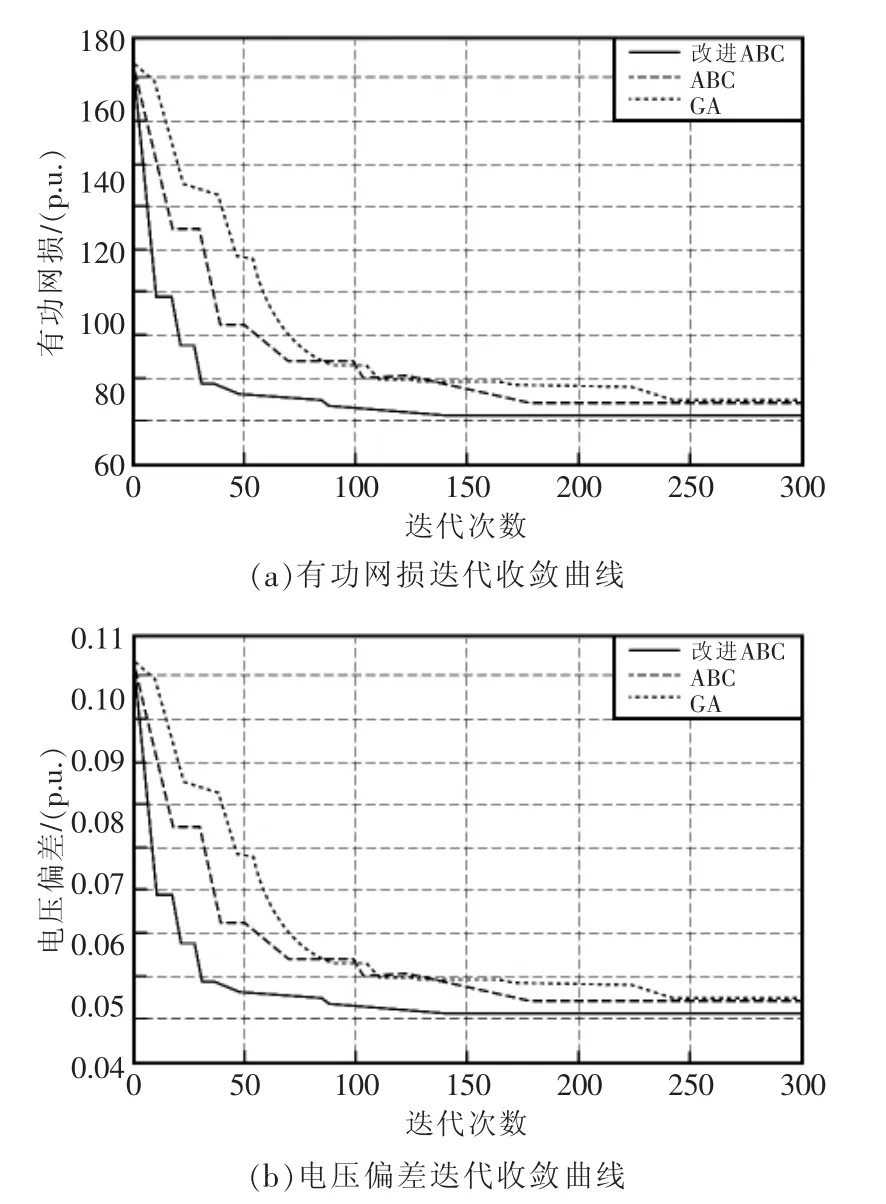
图4 优化算法收敛特性曲线Fig.4 Optimization algorithm convergence characteristic curve

图5为IEEE-33节点测试系统在改进ABC算法优化前后，各节点电压分布情况对比图。从图中可以看出，优化前，配电网线路末端节点的电压有效值较低，电能质量较差，优化后，各节点电压得到有效补偿，尤其是配电网末端电压，提高了电能质量。

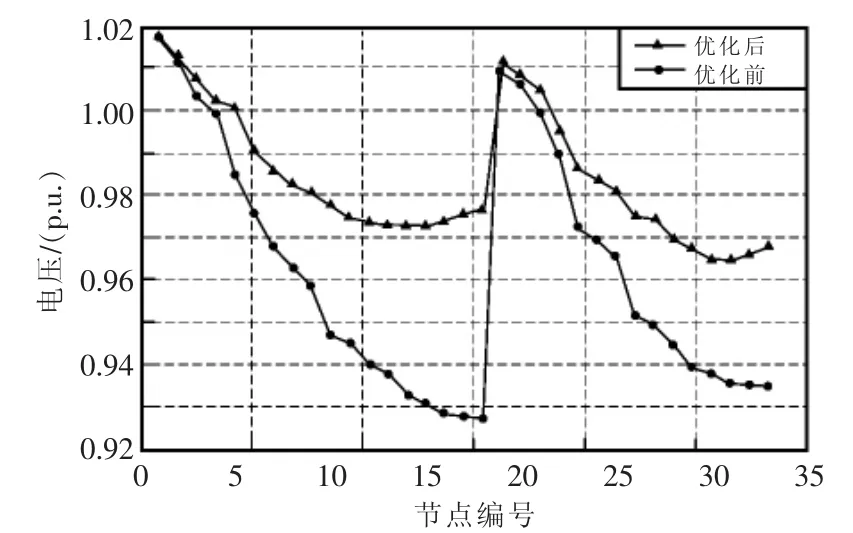
图5 优化前后节点电压对比Fig.5 Comparison of node voltage before and after optimization

4 结语

本文针对含DG的配电网无功优化问题，首先基于系统中DG与负荷的随机性问题，采用最优场景法模拟风机、光伏出力与负荷的波动性。然后建立了以网损、电压偏差最小为目标函数的数学模型，提出基于高斯变异和混沌扰动的人工蜂群算法，对模型进行优化求解。最后，在改进的IEEE-33节点配电网系统中进行分析。结果表明，该方法能够有效改善电能质量，提高电压水平，而且相比于GA、ABC算法，改进ABC算法收敛速度更快，搜索精度更高，性能更优。