永磁同步电机新型趋近律滑模变结构控制

欧阳凡，陈 林

（武汉科技大学 信息科学与工程学院，武汉 430081）

永磁同步电机（PMSM）因其结构简单、体积小、效率高等优点，被广泛地应用于众多领域。为了进一步提高PMSM调速系统的控制性能，滑模控制在一定的范围内得到了应用[1-5]，但传统滑模控制不可避免会产生高频抖振，削弱抖振成为提高PMSM滑模控制性能的重要方法之一[6]。文献[7]在变指数趋近律的基础上引入了饱和函数来代替符号函数，能够削弱系统的抖振。文献[8]提出了一种新的双幂次组合函数趋近律，使滑模变量在有限时间内收敛到稳态误差内，且减少稳态误差。文献[9]基于反双曲正弦函数，根据系统的状态变量，采用变带宽趋近方式，提出一种新型趋近律，有效地抑制系统的稳态转矩脉动。文献[10]是将幂次趋近律和变速趋近律结合在一起，有效地削弱系统的抖振现象。以上文献的趋近律存在到达滑模面时间过长的问题，且系统的控制律均为积分形式，但没有涉及系统的抗积分饱和。

针对以上问题，本文设计了一种新型趋近律。该趋近律引入一种新型饱和函数取代符号函数，由变速趋近律与幂次趋近律结合而成。在此基础上，加入反馈抑制抗积分饱和的控制。经过仿真验证，该方案可以很好的削弱系统的抖振，抑制了电机速度的超调量，增强系统的鲁棒性。使得系统具有良好的稳态性能与动态性能。

1PMSM数学模型

建立永磁同步电机数学模型，电机在d-q旋转坐标系中的定子电压方程为

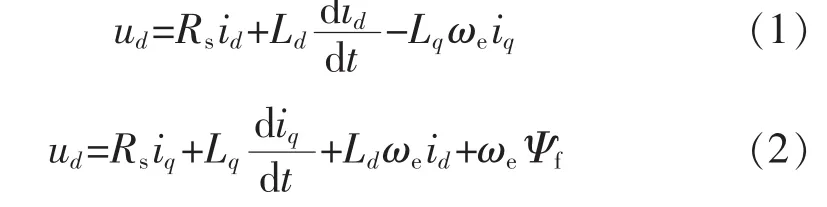
式中：ud，uq分别为 d，q 轴电压；id，iq分别为 d，q 轴电流；Ld，Lq分别为 d，q 轴电感；Rs为定子相电阻；Ψf为转子永磁体磁链；ωe为转子电角度。

电磁转矩方程为

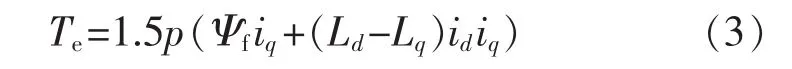
运动方程为

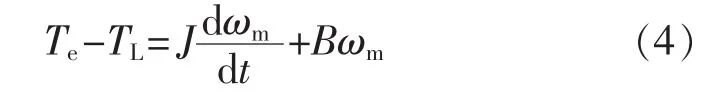
式中：Te为电磁转矩；TL为负载转矩；p为极对数；J为转动惯量；B为摩擦系数；ωm为转子机械角速度，且 ωe=pωm[6]。

2 滑模变结构速度控制器设计

2.1 设计滑模变结构速度控制器

将PMSM速度控制系统的角速度误差eω和角速度误差的导数分别定义为状态变量x1和x2。选择id=0控制策略作为永磁同步电机系统的控制策略。将q轴的电流iq作状态输出。

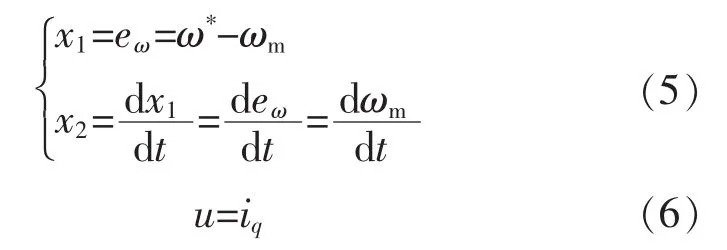
式中：ω*为给定机械角速度。

由式（3）～式（6）可以得到速度环控制系统的状态空间方程为

本文选取一般滑模面：

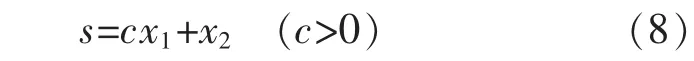
常用的趋近律有指数趋近律、幂次趋近律和等速趋近律等，但以上趋近律都存在不足。等速趋近律在削弱抖振与缩短到达时间之间存在比较大的矛盾。幂次趋近律可以很好地减小抖振，但到达的时间比较长。而指数趋近律中存在的等速项使得系统的抖振无法消除。

在文献[10]的基础上，本文提出一种变速幂次趋近律，使得系统能够在削弱系统的抖振同时加快系统到达滑模面的时间。其具体形式为

式中：k1＞0；k2＞0；0＜α＜1。

该趋近律是由幂次趋近律与变速趋近律组成的。当系统远离滑模面时，此时系统是按照幂次趋近律与变速趋近律的速率趋近滑模面，这样有效地增强了系统在远离滑模面时的趋近速率。当系统接进滑模面时，相比于文献[10]，本文趋近律不存在无法到达滑模面的分量，参数变少，缩短系统到达滑模面的时间。这样既能保证系统到达稳态的时间短，又能削弱系统的抖振。

将式（9）分为两部分：

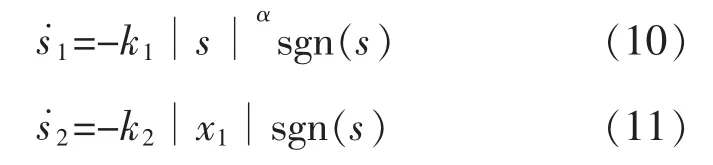
对式（10）两边同时积分，可以得到系统由初始状态s（0）到达滑模面的时间t1为[11]

对式（11）两边同时积分，可以得到系统由初始状态s（0）到达滑模面的时间t2为

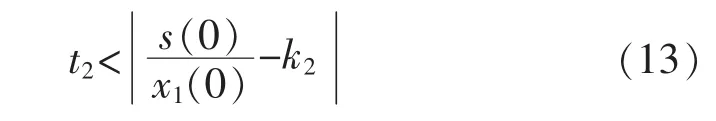
本文所选的趋近律到达滑模面所需的时间ta为

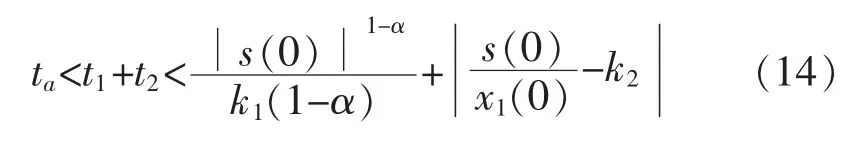
令˙3=-k3｜x1｜s，两边同时积分得：

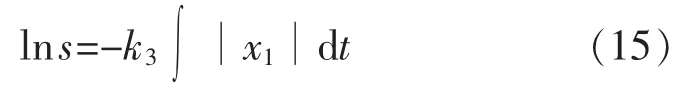
由式（15）可以得到s≠0，即文献[10]中的趋近律的变指数项无法到达滑模面，而本文的趋近律是可以在有限时间内达到滑模面的。

为了得到带宽，将式（9）离散化得到：

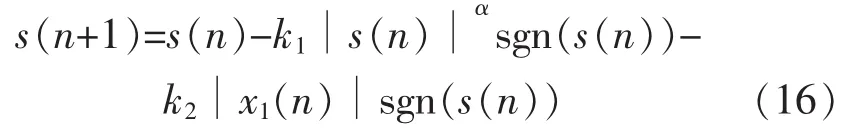
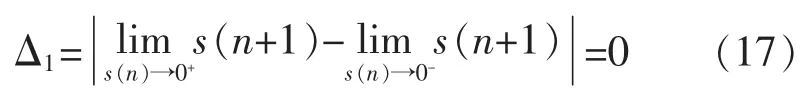
同理可以得到文献[3]中所示趋近律得带宽为

由式（16）与式（17）可以得到 Δ1=Δ2，即两种趋近律在理论上都可以达到无抖振。

系统到达滑模面后，为了加快抖振削弱，本文在文献[12]的特殊免疫函数的基础上引入了一种新的连续性函数f（s）来替代幂次趋近律中的开关函数sgn（s）。f（s）表达式为

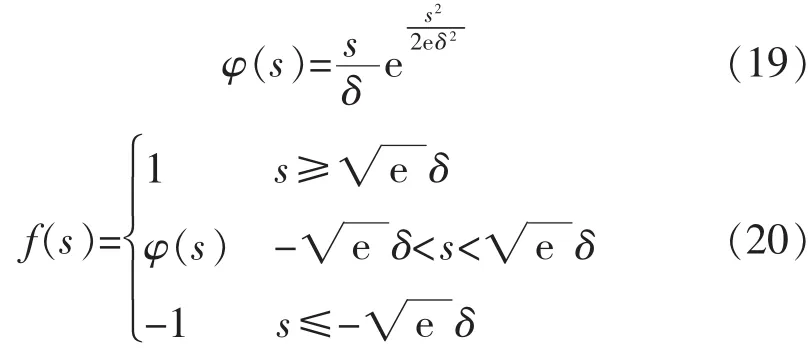
式中：δ＞0；e为自然对数的底数。

图1为新的符号函数与普通的符号函数对比仿真图。从图中可以看出，新符号函数变化比较平滑，不存在普通符号函数因跳变而存在的抖振问题，由此可以比较好的削弱系统的抖振而且不会对系统到达稳态的时间产生很大的影响。

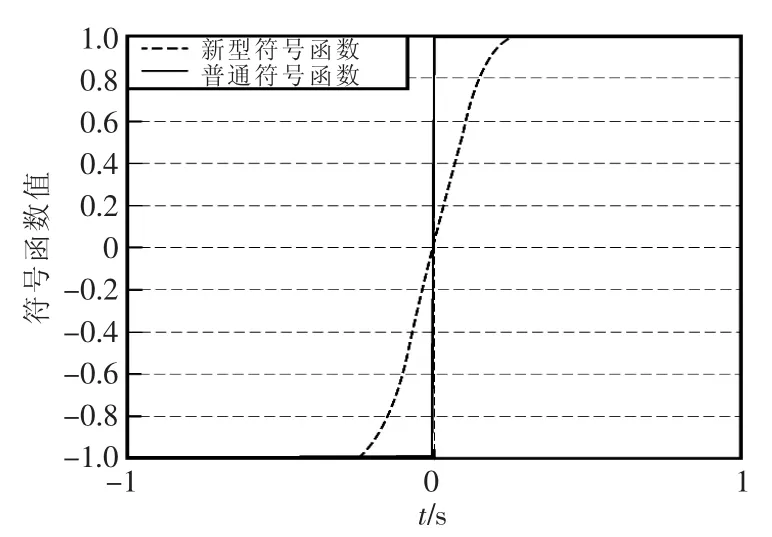
图1 两种符号函数对比图Fig.1 Comparison of two symbolic functions

将式（7）中的e作为系统的扰动，由式（7）～式（9）得系统的控制律：

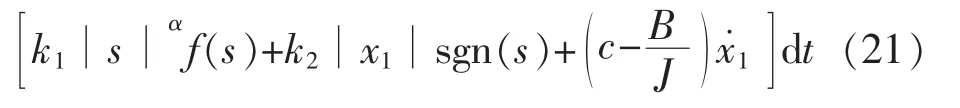
由式（21）可以看出，系统的控制律可以看作是一种积分。当控制器的输出iq达到了电机的电流限定值iqmax后，系统输出存在积分饱和现象，这会促使电机的速度的超调量过大。本文在滑模控制上加入了抗积分饱和方案，如图2所示。

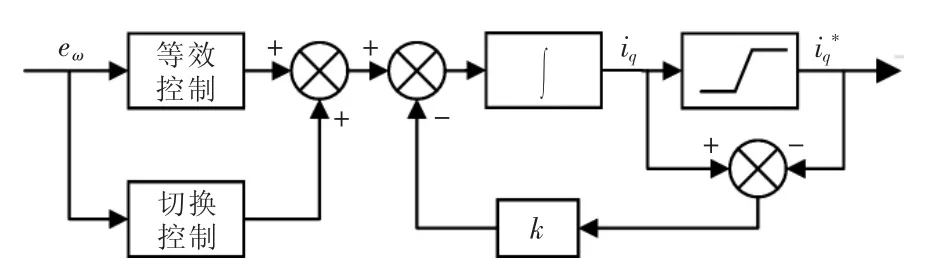
图2 滑模抗积分饱和控制系统框架Fig.2 Frame diagram of sliding mode anti integral saturation control system

图2中iq为系统通过控制律得到的输出，iq*为iq经过饱和输出后的输出。当iq*=iq时，此时系统没有进入饱和状态。当iq＞iq*时，此时系统进入了积分饱和状态，利用抗积分饱和策略，这能够很好地削弱系统的超调量。由图2可知利用抗积分饱和的滑模控制系统的控制律为

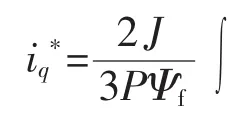
2.2 稳定性分析

即满足滑模控制到达条件。

将式（9）代入到式（23）中，得：

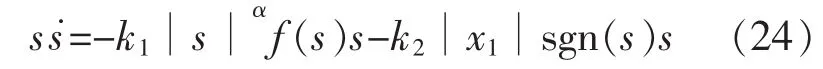
式中：k1＞0，k2＞0，0＜α＜1。

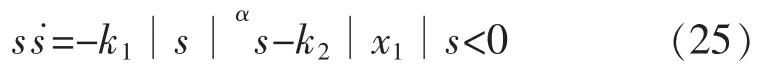
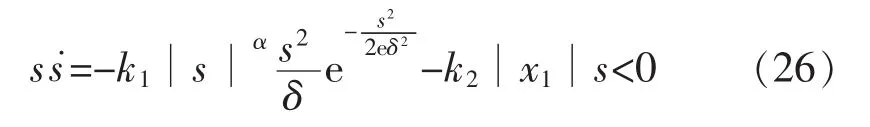
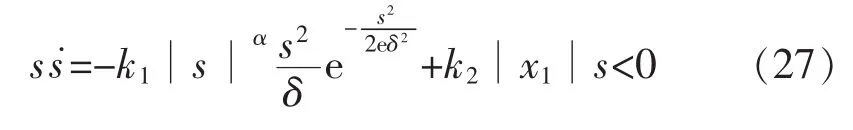
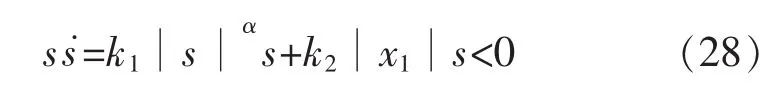
综上所述，s与s˙异号，本文趋近律满足稳定性条件，能够保证系统能够进入滑动模态。

3 仿真实验

PMSM滑模调速系统的结构框图如图3所示。在Matlab环境下建立系统的仿真模型进行仿真。电机的仿真参数：额定转速为1000 r/min，定子电阻为0.985 Ω，定子直轴电感 Ld为5.25 mH，定子交轴电感Lq为 12 mH，极对数为4，转子磁通 Ψf为0.1827 Wb，转动惯量 J为 0.003 kg·m2，阻尼系数 B为 0.008 N·m·s。

仿真条件设置：直流侧电流Udc为311 V，PWM开关频率 fpwm为 10 kHz，采样周期 TS为 10 μs，仿真时间为0.4 s。在0.2 s时，将电机的负载从0 N·m增加到10 N·m。电机的电流限幅值为-30 A～30 A。

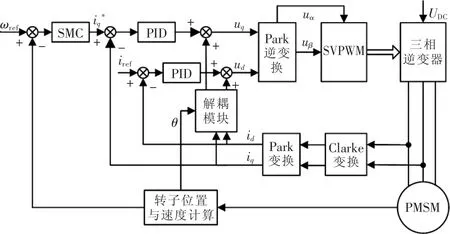
图3 PMSM滑模调速系统结构框图Fig.3 Block diagram of PMSM sliding mode speed regulation system

滑模速度控制器的参数为k1=2000，k2=3000，c=600，δ=0.25。抗积分饱和参数为K=15。仿真结果如图4～图7所示。

图8～图11为一般指数趋近律滑模控制仿真结果图，一般指数趋近律的形式为

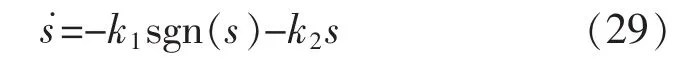
仿真参数为 k1=200，k2=300，c=30。

分析以上仿真波形可以看出：

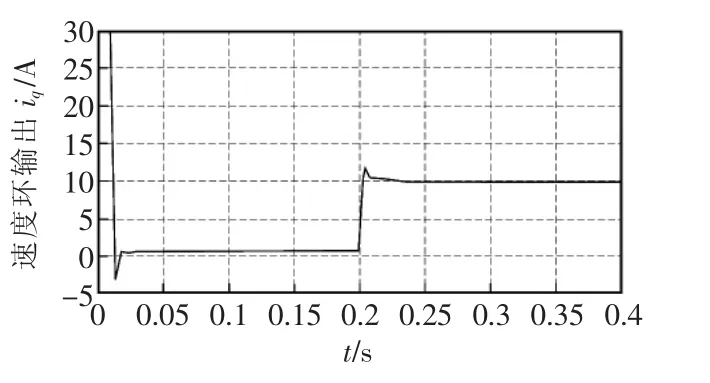
图4 新型趋近律抗饱和滑模速度环控制输出Fig.4 New reaching law anti saturation sliding mode speed loop control output

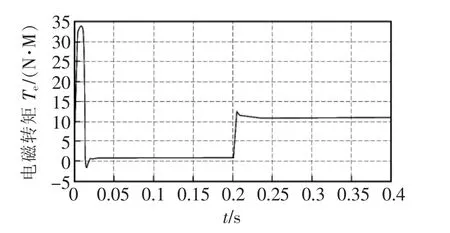
图5 新型趋近律抗饱和SMC转矩响应Fig.5 Torque response of the new reaching law anti saturation SMC

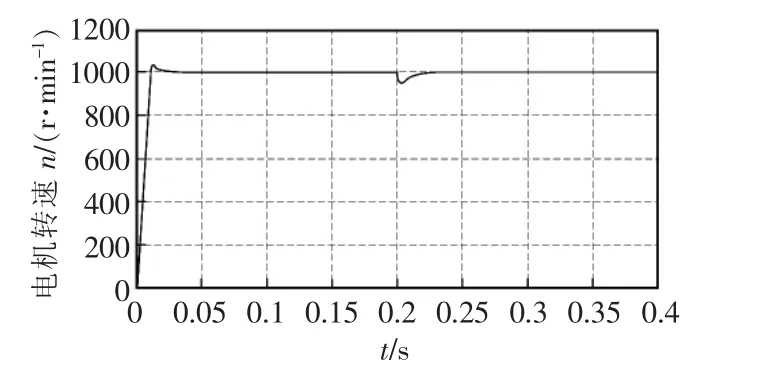
图6 新型趋近律抗饱和SMC转速响应Fig.6 Speed response of the new reaching law anti saturation SMC

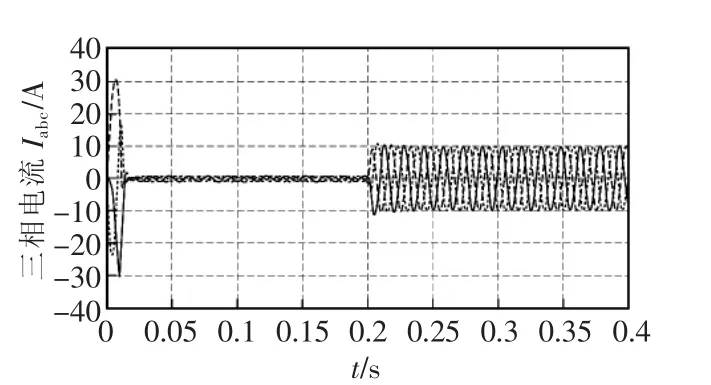
图7 新型趋近律抗饱和SMC三相电流响应Fig.7 Three phase current response of the new reaching law anti saturation SMC

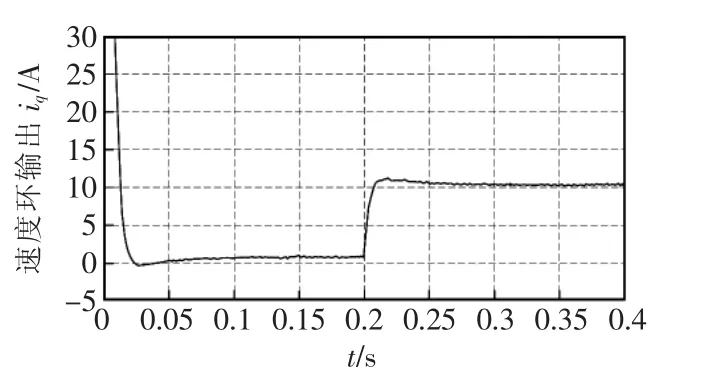
图8 一般指数趋近律SMC控制iq*响应Fig.8 General exponential reaching law SMC response iq*

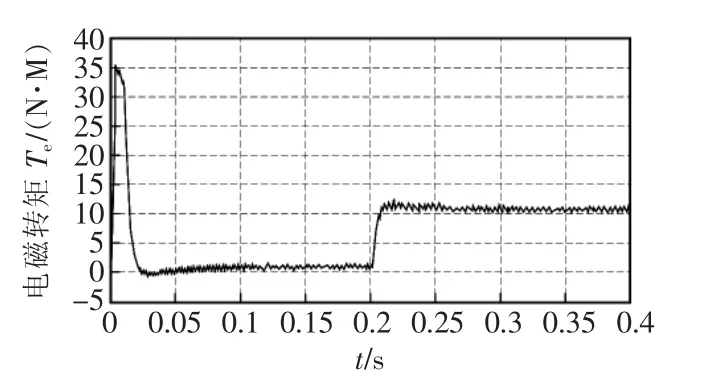
图9 一般指数趋近律SMC控制电磁转矩响应Fig.9 Electromagnetic torque response of the general exponential reachinglaw SMC

图10 一般指数趋近律SMC速度响应Fig.10 Speed response of the general exponential reaching law SMC

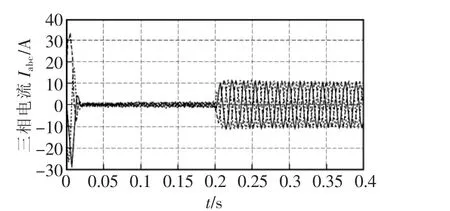
图11 一般指数趋近律SMC三相电流响应Fig.11 Three phase current response of the general exponential reaching law SMC

（1）在电机启动的时候，电机的电流达到限幅值，新型趋近律抗积分饱和滑模控制器的作用下，转速能够在0.02 s到达给定速度，且超调量小。转矩的抖动幅度比一般指数趋近律滑模控器的抖动幅度小。控制器的输出值iq*也能够很快的到达稳定状态。

（2）在0.2 s时，电机突加负载，此时电机的电流是没有达到限幅值，抗积分饱和控制不起作用。对比以上仿真结果图可知，新型滑模控制器作用下，电机能够很快的到达稳定状态。并且电机的转速下将比较小，转矩的抖动也很小。

4 结语

针对传统的一般指数趋近律在远离滑模面时的速度慢且到达滑模面时的速度过快的问题，本文在文献[3]的基础上，将幂次趋近律与变速趋近律结合在一起，并引入新的开关函数 f（s），得到新的趋近律。该方案能够加快系统趋近滑模面的速度，并且能够削弱系统到达滑模面后的抖动。相比较于文献[3]的趋近律，本文所选用的趋近律能够加快系统在滑模面上的抖振虚弱速度。由于文献[3]中没有考虑到系统的积分饱和问题，本文加入了反馈抗积分饱和控制策略。将新型幂次趋近律抗积分饱和滑模控制器应用到电机的速度控制中。仿真结果证明，本文的控制策略能够很好的削弱系统的抖振，缩短了系统的到达滑模面的时间，抑制了系统的超调量，改善了系统的稳态与动态性能。