基于BP神经网络的手写数字识别及优化方法

夏少杰，项 鲲

（浙江工业大学，浙江 杭州 310012）

0 引言

数字识别的应用十分广泛，尤其是手写数字识别，由于书写的随意性很大，造成在识别过程中具有一定的难度。随着近几年人工智能的火热发展，对于数字识别提出了很多方法，主要有统计、神经网络和聚类分析等，本文采用的方法是BP神经网络。这是一种前馈反向型神经网络，具有并行处理信息、自组织、自学习信息等优点。

1 Mnist数据集介绍

Mnist数据集是一个手写体数据集，里面包含了大量的手写体图像，如图1所示。

图1 Mnist数据集示例

整个数据集包含了60000行的训练数据集（mnist.train）和 10000 行的测试数据集（mnist.test）。每张图片包含28×28个像素，将此数组展开成一个向量，长度是28×28=784。因此在Mnist训练数据集中mnist.train.images是一个形状为 [60000，784]的张量（如图2所示），第一个维度数字用来索引图片，第二个维度数字用来索引每张图片中的像素点。图片里的某个像素的强度值介于0～1之间。

图2 Mnist训练集数据格式

Mnist数据集的标签是介于0～9的数字，把标签转化为“one-hot vectors”，一个one-hot向量除了某一位数字是1以外，其余维度数字都是0，比如标签 0 将表示为（[1，0，0，0，0，0，0，0，0，0]），标签 3将表示为（[0，0，0，1，0，0，0，0，0，0]）。 因此，mnist.train.labels是一个[60000，10]的数字矩阵。如图3所示。

图3 Mnist训练集标签数据格式

2 神经网络的设计

2.1 神经网络介绍

人工神经网络是20世纪80年代在生物神经系统研究的启发下发展起来的一种信息处理方法，是由大量简单神经元所构成的非线性动力学系统，它处理信息的方式类似于动物大脑的处理方式，即是一种利用神经元之间的突起来进行信息传递的数学模型。国际著名的神经网络专家、第一个计算机公司的创始人和神经网络实现技术的研究领导人Hecht-Nielson给神经网络的定义是：“神经网络是一个以有向图为拓扑结构的动态系统，它通过对连续或断续式的输入作状态响应而进行信息处理”[1]。

BP（Back Propagation）神经网络（简称 BP 网络），是一种反馈型学习网络：输入层各神经元负责接收来自外界的输入信息，并传递给中间层各神经元；中间层是内部信息处理层，负责信息变换，根据信息变化能力的需求，中间层可以设计为单隐含层或多隐含层结构，最后一个隐含层传递到输出层各神经元的信息；经进一步处理后完成一次学习的正向传播处理过程，由输出层向外界输出信息处理结果。当输出值和实际值之间的误差大于预定误差值时，网络进入误差的反向传播阶段，误差通过输出层，按误差梯度下降的方式修正各层权值，向隐含层、输入层逐层反传[2]。周而复始的信息正向传播和误差反向传播过程，是各层权值不断调整的过程，也是神经网络学习训练的过程，这个过程一直持续进行，直至到网络输出的误差减少到预定误差范围内，或训练次数达到预先设定值[3]。

2.2 神经网络基本理论

2.2.1 人工神经元模型

神经网络的基本信号处理单元是人工神经元，是对生物神经元的近似仿真。其模型如图4所示，表示了一种简化的人工神经元结构。其输入输出关系可描述为[4]：

式中，xj（j=1，2，…，n）是从其他细胞的输出传来的输入信号；θ为阈值；权系数wj表示连接的强度，就像生物细胞中突触的负载，数值为正表示激活，数值为负表示抑制；f（I）称为激活函数。

图4 神经元结构模型

2.2.2 激活函数

激活函数是神经网络中的重要组成部分，由于线性模型的表达能力不足，采用激活函数可以导入非线性因素，使神经网络具有更好的表达能力。常见的激活函数如图5所示。

图5 激活函数

2.2.3 BP算法

误差反向传播算法（back-propagation algorithm）简称为 BP算法[5，6]。BP网络含有输入层节点、输出层节点和隐含层节点。其激活函数通常选用连续可导的Sigmoid函数：

在系统辨识中，神经网络模型通常选用多层并行网的形式，即多层BP网。它的工作原理如下：输入信号经过输入层后的输出信号，传递给隐含层的节点，通过激活函数作用后，把隐含层节点的输出信号传递给输出层接点，通过激发函数作用后产生出输出信号，即为神经网络模型的输出ym。如果输出层的输出有较大误差，则会将误差信号反馈到输入端。按照误差信号修改各层权值，当过程的输出yp与神经网络模型的输出ym之间的误差小于一定值时，停止辨识。

2.3 BP网络设计

本文采用包含隐含层的BP网络对数字识别进行仿真。由于样本训练矩阵是784维的，设定输入层有784个神经元，通过反复试验，隐含层设计两层，第一层包含500个神经元，第二层包含300个神经元。对于输出层，由于需要识别0～9共10个字符，输出层设为10个神经元。根据Mnist数据集的标签，输出端采用“one hot”编码，例如，对于输出结果“4”，它的输出端结果为（0，0，0，0，1，0，0，0，0，0）。

因此，本文设计的 BP网络为 784×500×300×10的结构。按照BP网络的一般设计原则，中间层神经元的传递函数为双曲正切函数tanh。由于输出已被归一化到区间[0，1]中，因此输出层神经元的传递函数可以设定为softmax函数。

采用以上网络结构对Mnist数据集进行训练得到的测试结果如图6所示。

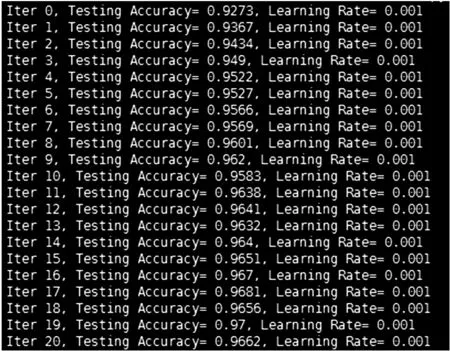
图6 Mnist测试集测试结果

3 神经网络的优化

对于本文构建的神经网络，可以从以下几个方向作进一步优化。

（1）初始化权值

一般情况下构建神经网络采用随机采样点的初始化方式，但是如果输入神经元个数很多的情况下采用正态分布的随机数初始化可以有效加速网络的收敛。

（2）针对当前的网络层设置Dropout

Dropout的意思是在训练过程让一定比例的神经元失效（取值一般是0～1之间的数），这个函数的使用场景是当网络设计比较复杂时，容易出现过拟合现象，通过设置Dropout可以减小网络复杂度，有效防止过拟合。

（3）选取不同的激活函数

针对不同神经网络，激活函数也会影响网络的优劣。tensorflow中封装了很多激活函数，主流如relu、softmax、sign等，在调试过程中可以尝试不同激活函数来构建网络，有些情况下可以大幅提升模型的精度。

（4）选取不同的代价函数

代价函数的不同也会影响到模型收敛的速度与精度。本文设计的网络通过测试发现采用交叉熵代价函数可以得到最优模型，常见的还有SSD（差值平方和）、SAD（绝对误差和）等。在具体项目中可以根据构建网络的特性来选择合适的代价函数。

（5）采用不同优化器来最小化代价函数

优化器选取的不同直接影响了网络模型收敛的速度和是否会陷入局部最优解，在tensorflow中封装的优化器，如图7所示。选择不同的优化器对网络的收敛速度和精度会有直接影响。

图7 tensorflow中封装的优化器

（6）学习率的设置

一般而言，学习率的设置不能过大或过小，过大会导致损失函数没法收敛到一个极小值，而过小会使得收敛速度变慢。因此，本文在网络优化时设置学习率随着迭代次数的增加逐渐变小，这样一方面可以在训练的前期使模型快速收敛，同时又可以在训练后期让模型收敛到一个理想值。

下图8是对本文设计的神经网络优化后的测试结果。从图6与图8的对比可以发现，优化后的识别精度达到了98.3%，比优化前提升了1.3%左右。

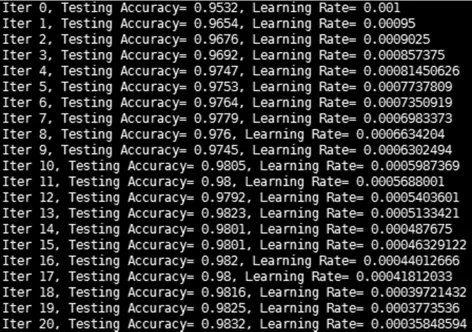
图8 优化后的测试结果

4 结语

BP算法因其简单、易行、计算量小、并行性强等优点，是目前神经网络训练采用最多也是最成熟的训练算法之一。本文主要描述了BP网络在手写数字识别中的应用，提出了若干条优化方法，并通过实验获得了优化后的结果。但BP算法同样存在学习效率低、收敛速度慢、易陷于局部最小状态等缺点，需要进一步完善和改进。

为了进一步提升手写数字的识别精度，作者后续会在神经网络中引入卷积层，通过卷积层和全连接层的组合来提取图像中的深层特征，进而训练出识别精度更高的网络模型。