地基导航系统高性能快速定位算法

郭丽， 张雪， 郭熙业

(1.湘潭大学 信息工程学院,湖南 湘潭 411105;2.国防科技大学 智能科学学院,湖南 长沙 410073)

0 引 言

全球导航卫星系统(GNSS)能够提供范围广泛全天候的导航、定位和授时服务,但其信号容易受到阻塞和干扰,导致性能下降甚至无法使用[1]．为了解决这个问题提出了使用伪卫星定位[2]的新概念．但是前期使用非同步伪卫星的实时厘米级定位只能通过无线调制解调器(如标准RTK-GPS)向流动站单元提供数据的基站实现[3]．Locata系统中所采用的时间同步解决方案不同于传统伪卫星定位系统,它可以在没有外部参考站和数据链路的情况下完成高精度时间同步组网[4].Locata系统中的TimeLoc技术,是一种精确的时间同步技术,它能使系统时钟达到ns级的同步精度[5].但是,对于其他地面导航系统而言,准确的时间同步需要对设备延迟进行精确的校准,从而大大增加了工程实施的难度．基于此,国防科技大学的郭熙业[6]搭建的新型地基导航系统,提出了一种不依赖于准确的站间时间同步的新的地基伪卫星定位方法，以较低成本及复杂度,实现系统整网高精度时间同步,有效支撑地基导航系统实现精密单点定位．

但地基伪卫星单独定位系统存在一个急需要解决的问题是，基站固定情况下,观测矩阵行列式之间有较强的相关性,导致观测方程病态,在短时间内定位失败，因而需要观测比较多的历元才能实现定位解算[7]．

基于此,本文提出了一种利用空中移动伪卫星辅助地面伪卫星并利用TIKHNOV正则化相结合进行定位的方案,该方案利用无人机机动能力强,飞行轨迹控制能力强,适合作为导航平台的优点，将其应用在伪卫星定位系统之中．本文对该方案的性能进行了仿真分析,结果表明,该方案可以有效地提高定位精度,减小定位时间,是一种实现地基伪卫星快速有效的定位方法．

1 单差载波相位观测模型

由于载波相位测量值的精度比伪距测量值的精度要高出几个数量级,因而基于载波相位的差分系统通常具有最高的定位精度,可以用来实现精密定位[8]．本文采用星间单差载波相位观测模型进行定位解算,因为地基伪卫星距离地面的高度较低避免了电离层误差的影响,单差去除了伪卫星间钟差，同时忽略对流层和接收机钟差的影响, 其载波相位观测方程模糊度参数本身是有整数性质的．但是由于伪卫星端和接收端的初始相位和载波相位硬件延迟是未知的,在实际处理的过程中,这些误差值被模糊度值吸收,使得模糊度值不再具有整数的性质．利用载波相位测量值实现精密定位的根本任务就是正确快速的求解出载波相位测量值中的整周模糊度．单差观测方程[6,9]为

Δz=ACCΔxC+ANNΔxN+ε,

(1)

式中:ε为单差残差向量;ACC为m×3的待求坐标系数矩阵,m表示伪卫星数目减1；ANN为m×m的单位阵;ΔxC为三维未知点坐标改正值向量;ΔxN为单差模糊度向量;Δz为常数向量．

本文采用在航解算(OTF)求解整周模糊度,令ACN=[ACCANN],ΔxCN=[ΔxCΔxN],其中ACN为(nm)×(3n+m)维矩阵,ΔxCN为3n+m维的列矩阵,n为观测历元数．根据最小二乘得到未知参数的浮点解表示如下:

=N-1ACNRZZΔz,

(2)

式中:RZZ为误差系数的先验权矩阵;N为法矩阵；N-1为最小二乘的方差—协方差矩阵．

2 增强模糊度浮点解算方案

为了解决模糊度观测方程病态的问题,本文采用载波观测方程进行定位解算,通过加权最小二乘获得模糊度浮点解和协方差矩阵,根据OTF模型解算特性提出特定的TIKHNOV正则化矩阵来改善法矩阵奇异值之间的差值较大的问题．并通过加入空中移动伪卫星平台减小法矩阵行列式之间的相似性,从而得到精度较高的模糊度浮点解,使得LAMBDA算法[10]对模糊度固定成功率增加．

2.1 TIKHNOV正则化

TIKHNOV正则化其本质是增加一定的约束,补充先验信息,将病态问题转化为稳定问题．式(2)最小二乘估计得到的正则化估计为

‖ACNΔXCN-ΔZ‖2+αΩ(ΔXCN)

=min，

(3)

式中:α为正则化参数;Ω(ΔXCN)为稳定范函;R为正则化矩阵;‖·‖表示二范数．针对模糊度在航解算模型其系数矩阵的特点,提出一种适用于此模型的正则化矩阵的求取方式．

(4)

将N进行奇异值分解之后S是奇异值的降序排列,根据法矩阵奇异值的特点将S矩阵进行分块处理．

(5)

S2中(2n+m)×(2n+m)对角元素所代表的奇异值很小,在S1和S2之间有一个较大的跳跃,导致法矩阵病态,方程的条件数很大．

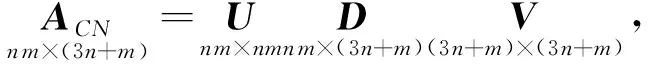
(6)

(7)

(8)

选定正则化矩阵R之后,应用L曲线法进行大量计算,选取平滑因子α=1时效果最好[8]．所以求解等式变为:

(9)

2.2 增加高空移动伪卫星辅助平台

仿真实验在无人机自身定位精度较高的情况及导航能力较强的情况下,使其在既定的轨道上运行．根据“一高四低”五站的布局方法对地面基站进行布站[11-13],定位系统示意图如图1所示.

无人机轨迹规划确定分为两个部分．1)首先确定无人机的飞行高度,选取地面固定基站的重心点的横纵坐标,在无人机能够安全飞行的最大高度值中通过仿真对比选取几何精度因子(GDOP)最优点作为无人机飞行高度确定．2)为了研究的方便和可行性,设定无人机的运行方向与接收机预测运行轨迹方向一致．预估接收机的运动轨迹,将无人机的轨迹设定和接收机轨迹类似,在高程平面上随机选择一点作为无人机运动的起始点．无人机本身搭载了双余度惯导模块,实时动态(RTK)模块,以及雷达测距模块,能够精确地感知当前姿态及位置信息,实现厘米级定位定高,能够按照设定的航线飞行．将预设轨迹坐标作为无人机轨迹参考真值．为了减少观测中出现的多普勒效应,无人机的速度选择一个在历元间隔之间无人机位置坐标变化明显且相对较小的值．

3 仿真结果与分析

本文从三个方面验证所提方案的优越性,通过对比其观测方程的法矩阵条件数的改善情况和基线浮点解定位结果精度[14],模糊度精度衰减因子(ADOP)值结果差异,验证本文提出的方法能够极大程度地提高工作效率和定位精度．通过三个阶段的仿真实现演算．

步骤1:传统OTF(仅地面固定基站)．

步骤2:地面固定站+TIKHNOV正则化．

步骤3:地面固定站+空中移动站+TIKHNOV正则化．

3.1 法矩阵条件数

使用条件数K来判断加入无人机搭载平台之后对求解方程病态性的改善情况:

K=‖N-1‖‖N‖,

(10)

条件数也度量了法矩阵特征值的分散情况,条件数越小,法矩阵求逆越稳定,即可以得到更精确的浮点解．

3.2 基线浮点解定位结果

在王振杰博士的论文[15]中通过正则化能够达到模糊度浮点解改善的目的已经得到验证．本文采用:

(11)

空中移动站的加入,使得接收机出现高仰角,且使得整个定位区域的水平精度因子(HDOP)值得到改善．以无人机运动的某一个时刻为例,场水平HDOP分布如图3所示.

通过图3可以很明显地发现,加入空中辅助基站之后定位区域的HDOP值有了明显的改善,从而使得在测量误差相同的情况下,定位精度得到提升．

定位浮点解与真实轨迹点(初始设定的接收机运行轨道坐标点)做差得到三维误差,其结果如图4所示.

图4中圆圈标记的点表示定位失败的点,通过对矩阵条件数的改善,加入空中移动基站之后所需收敛时间明显小于只有地面固定基站．以某历元前后5个历元定位精度都达到厘米级作为初始收敛历元的判断依据,在误差条件一致的情况下实验结果表明:在固定基站的情况下,正则化的加入使得在一定历元时间内定位精度比其高出一个数量级．当加入空中移动基站之后的首次收敛时间明显提前,其定位精度也有所提高．

3.3 ADOP

使用ADOP来描述哪一组模糊度具有较高的定位精度,具有较小ADOP[16]的模糊度浮点解其成功固定的可能性越大．

(12)

图5示出了在只有固定基站作用的时候正则化对于提高模糊度固定率有着很好的作用．当加入空中移动基站之后,ADOP在短历元时刻已经达到一个相对较好的效果．

4 结束语

针对单差伪卫星定位系统法方程条件数大，求逆不稳定和求解所需观测时间长的问题,设计了相应的TIKNOV正则化矩阵以改善法方程的病态性,并通过加入空中移动的定位基站平台,获得可靠的协方差矩阵,并通过对模糊度精度因子的计算验证了此方法提高了模糊度的固定概率．算例结果表明正则化的贡献是有限的,主要贡献实质上还是空基移动平台的加入,显著改善了定位的几何图形结构从而大大减少首次收敛所需的时间,提高模糊度浮点解的精度,减小浮点解定位误差,两者相结合能够极大程度的提高系统定位性能．

本文为地面伪卫星系统的设计提供了一个新的思路,适用于各种类型的地基导航系统．