基于GPS的分段式高程拟合实验及分析

2019-01-10张涛陈梦张丕亚

全球定位系统 2018年6期

张涛,陈梦,张丕亚

(山东科技大学测绘科学与工程学院,山东青岛 266000)

0 引言

高程基准在国民基础建设中有着广泛的应用,例如跨河桥梁建设中的高程基准传递、矿区各级控制点的高程基准传递[1].传统的高程传递方法如静力水准法、动力水准法和常规大地测量等方法效率不高、精度低、且受测量环境影响较大[2].GPS测量技术具有全天候、快速、准确的优点, GPS精密大地高测量精度可达毫米级[3],这就为GPS高程应用提供了先决条件,于是如何将GPS测量得到的大地高转换为高程通用的正常高成为关键问题.

目前,GPS高程拟合的主要研究集中于利用诸如多项式曲面拟合、多面函数拟合、半参数拟合等模型进行大地高与正常高的转换[4].此外还有利用地面重力数据与GPS拟合模型相结合的组合法进行高程拟合[5].以上方法大多专注于数学模型的选取与应用,因此有模型计算经验性和重力数据分布不均匀等问题[6],本文在常用GPS高程拟合模型的基础上,利用部分矿区GPS测量数据,采用了分段式高程拟合的方法.通过计算得出:合理分段拟合高程的方法相较于整体式传递具有一定的优越性.

1 高程拟合原理及方法

GPS测量所得高程为以参考椭球面为基准的大地高(H),我国工程使用的高程为以似大地水准面为基准的正常高(h).似大地水准面与参考椭球之间的差距称为高程异常(h),则H与h存在如下关系:

H=h+ξ.

(1)

高程异常(ξ)主要通过函数拟合获取,常用函数拟合方法有二次曲线法、二次曲面法、多面函数法等.

1.1 二次曲面法

曲面拟合法是认为高程异常在一定范围内变化平缓的前提下,将高程异常在一定范围内近似看作是个点坐标的曲面函数,用这个拟合函数计算其他GPS点高程异常,进而求取正常高[7].

在曲面拟合法中,设点的高程异常ξ和平面位置坐标x,y有如下关系:

ξ=f(x,y)+ε.

(2)

式中:f(x,y)为ξ的中趋势值,即拟合出的似大地水准面;ε为拟合残差[8].

对于f(x,y)通常取一个n次插值多项式函数

f(x,y)=a0+a1x+a2y+a3xy+a4x2+

a5y2+…+anxn.

(3)

式中:a0,…，an为拟合系数；x,y为点的平面坐标.

式(2)的矩阵形式为

ξ=XA+ε，

(4)

式中:ξ=(ξ1，ξ2，…，ξn)T;

A=(a0，a1，…，an)T；

ε=(ε1，ε2，…，εn)T；

对于每个已知点都可以列出上述方程.依最小二乘法原理,在∑ε=min条件下可解得拟合系数A=(XTX)-1(XTξ).将求得的α代入式(7)中便可求得插值点位的ξ,从而得到待测点的正常高.

其中,假定测区的似大地水准面为二次曲面,取式(7)的前六项使其更符合似大地水准面的描述.则表达式为

f(x,y)=a0+a1x+a2y+a3xy+a4x2+

a5y2.

(5)

1.2 多面函数法

多面函数拟合法的基本思想:任何不规则的数学表面与不规则的圆滑表面,总可以用一系列有规则的数学表面总和,以任意精度逼近[9-10].其表达式为

(6)

式中：ai为待定参数;Q(x,y,xj,yj)为核函数,常用的核函数为

Q(x,y,xj,yj)=[(x-xj)2+(y-yj)2+σ2]K,

(7)

式中,δ为光滑因子,当K取1/2时模型为正双曲面函数,当K为-1/2时模型为倒双曲面函数.

设有n个已知点(xi,yi)(i=1,2,3,…,n),选其中m(m≤n)个点(xi,yi)(j=1,2,3,…,m)为核函数核心点,令Q(x,y,xj,yj)=f(xi,yi,xj,yj),则有:

(8)

其误差式的向量式为

V=Qα-ξ,

(9)

依据最小二乘原理可得:

α=(QTQ)-1QTξ.

(10)

2 高程传递实验

2.1 数据来源

本次试验采用某矿三等高程基准传递测量数据,测量方法采用C级GPS静态测量与三等水准测量相结合的方式.测区整体呈西高东低的走势,但高程差异不大即地形起伏不大.GPS网形如图1所示,经网平差与水准平差计算后的各点大地高与正常高如表1所示.

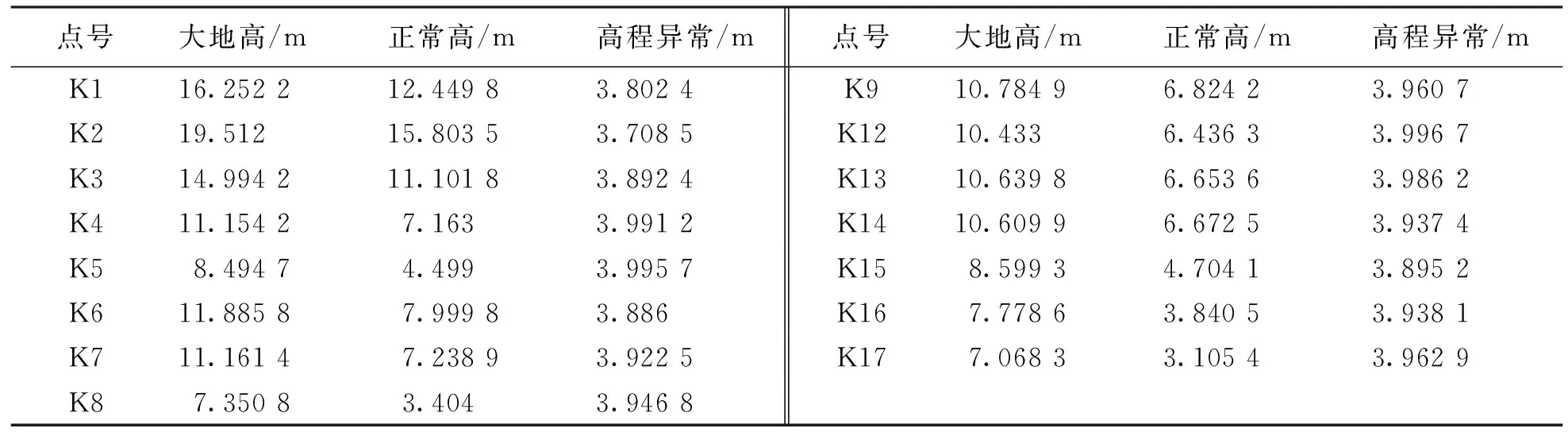
点号大地高/m正常高/m高程异常/m点号大地高/m正常高/m高程异常/m K116.252 212.449 83.802 4K910.784 96.824 23.960 7 K219.512 15.803 53.708 5K1210.4336.436 33.996 7 K314.994 211.101 83.892 4K1310.639 86.653 63.986 2 K411.154 27.163 3.991 2K1410.609 96.672 53.937 4 K58.494 7 4.499 3.995 7K158.599 34.704 13.895 2 K611.885 87.999 83.886 K167.778 63.840 53.938 1 K711.161 47.238 93.922 5K177.068 33.105 43.962 9 K87.350 8 3.404 3.946 8

2.2 高程传递方案

GPS网形即可以作为一个整体来处理,也可以切分成几部分处理[11].本次实验采用两种方式进行高程传递,即以拟合模型为基础的分两段式传递与以拟合模型为基础的整体式传递,其中K1、K2、K3、K4、K5、K8、K12、K13、K14、K15为已知点,K6、K7、K9、K16、K17为检核点.

2.2.1 分段式高程拟合

根据表1中各点高程异常可知,K1、K2、K3、K4、K14、K6点所在区域高程异常变化不是十分平稳的,而其余部分区域的高程异常变化相对稳定.故以K4点为界,针对左侧区域高程异常变化较大的特点选择多面函数拟合法,右侧高程异常变化平缓区域则选用二次曲面函数拟合法.

1) 采用多面函数拟合法,以K1、K2、K3、K4、K14五个核心点拟合出K6点的高程异常并依式(1)得到其正常高;因K4、K6两点距离较近且地形起伏不大,可利用K4点已知高程异常结合水准测量结果检验K6点的传递精度.

2) 采用二次曲面拟合法,以第一段拟合出的K4点的拟合值代替K6点的高程异常并与K4、K5、K8、K12、K13、K15共七个已知点拟合出K7、K9、K16、K17四个待定点的高程异常进而得到正常高.

2.2.2 整体式高程拟合

1)采用多面函数拟合法,以K1、K2、K3、K4、K5、K8、K12、K13、K14、K15为已知点进行拟合,以K6、K7、K9、K16、K17为检核点.

2)采用二次曲面拟合法,以K1、K2、K3、K4、K5、K8、K12、K13、K14、K15为已知点进行拟合,以K6、K7、K9、K16、K17为检核点.

分段传递高程结果与分别采用多面函数拟合法和二次曲面拟合法的整体拟合结果进行对比,高程传递实验流程如图2所示.

2.3 高程传递结果

利用MATLAB程序,对第一段和第二段分别采用多面函数法和二次曲面拟合法进行拟合;对整体分别采用多面函数拟合与二次曲面拟合.分段拟合结果如表2所示,整体拟合结果如表3所示.

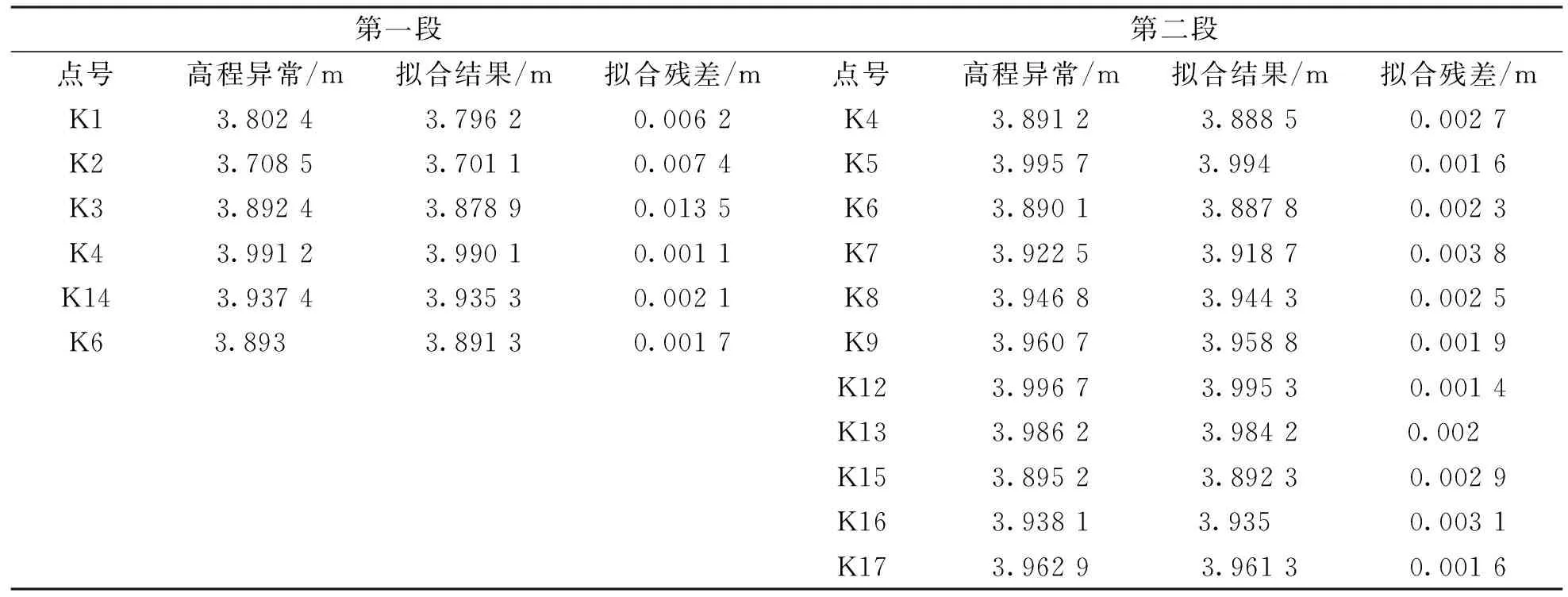
表2 分段拟合结果

表3 整体拟合结果

2.4 精度评定

1)内符合精度

内符合精度M内有如下计算式:

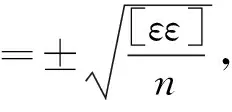
(11)

式中:ε为参与计算的已知点的拟合残差;n为参与计算的已知点的个数.

2)外符合精度

外符合精度M外有如下计算式:

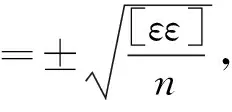
(12)

式中:ε为参与计算的检核点的拟合残差;n为参与计算的检核点的个数.

根据表2的拟合结果计算内符合精度与外符合精度[13],计算结果如表4所示.

表4 各传递方法精度对比

2.5 结果分析

依表2,分段拟合中第一段最大拟合残差为0.013 5 m,最小拟合残差为0.001 7 m.K4点与K6点拟合结果相差0.001 2 m,相差较小,故可以用K4点的拟合值代替第二段中K6点的拟合值作为已知点,第二段结果也间接表明K4已知点的稳定性.第二段最大拟合残差0.003 8 m,最小拟合残差0.0014 m.

依表3,多面函数整体拟合结果中最大残差为0.029 9 m,最小残差为0.007 9 m.二次曲面整体拟合结果中最大残差为0.042 1 m,最小拟合残差为0.007 2 m.

依表4,无论是内符合精度还是外符合精度,分段式高程传递精度均优于采用多面函数拟合法和二次曲面函数拟合法的整体传递.