波浪水质点可视化示踪教学实验装置

陶爱峰, 刘亚伊, 苏俊玮, 秦淑芳, 吴 迪, 徐 啸

(1. 河海大学 海岸灾害及防护教育部重点实验室, 江苏 南京 210098；2. 河海大学 港口海岸与近海工程学院, 江苏 南京 210098)

波浪理论是港口航道与海岸工程专业、海洋科学专业必修课的重要内容。其中微幅波理论是应用势函数来研究波浪运动的一种线性波浪理论,是波浪理论中最基本、最重要的内容之一[1]。由于微幅波理论包含一系列的假设与简化,初学者对其理解存在一定的困难,为提高学生对知识的吸收水平和实践能力,河海大学从2008年开始就设置了海岸动力学实验课,重点开展波浪有关实验。

水质点示踪是指利用人为制造的示踪剂替代水质点,将水质点的运动轨迹展示出来，并用摄像机等仪器拍摄记录。水质点的示踪研究是进一步探讨波浪与结构物相互作用的必要基础与关键步骤[2]。Longuet-Higgins[3]和渠时勤[4]分别利用固体浮子和液体示踪剂对波浪进行水质点示踪实验,但由于固体浮子的密度与水不相等、液体示踪剂易扩散污染水体等原因,示踪效果不是十分理想。针对波浪的运动学特性研究较多的是Grue等[5-7],他们从2003年开始基于Jessen等[8]开发的PIV流速测量系统,对波浪的波形速度、水质点速度以及加速度都进行了较为深入的研究。PIV测量系统虽然精细,但PIV整套设备过于昂贵,且对拍摄要求较高,难以广泛应用于本科生实验教学。基于水质点示踪技术现状,苏俊玮等[9]提出了一种结构简单、操作方便且成本低的水质点示踪装置,开展了对规则波的示踪实验,但并未对装置的适用性进行深入的分析。本研究结合受力分析以及文献[9]的示踪装置在海岸动力学实验课程的水质点示踪实验,探讨其对水质点水平速度示踪的适用性。

1 实验方法

1.1 实验装置

经过系列探索,本实验采用苏俊玮等[9]提出的示踪装置(见图1),该装置通过示踪粒子连接绳串接密度比水稍大的示踪粒子并与可移动支架相连接,使得示踪粒子可在流场中任意位置处于 “悬浮状态”,有效地改善了现有技术中示踪粒子沉降扩散等问题,且结构简单、操作方便,能直观体现任意水深处的水质运动轨迹[9]。在使用该示踪装置前,对其进行受力分析,以验证该装置的有效性。

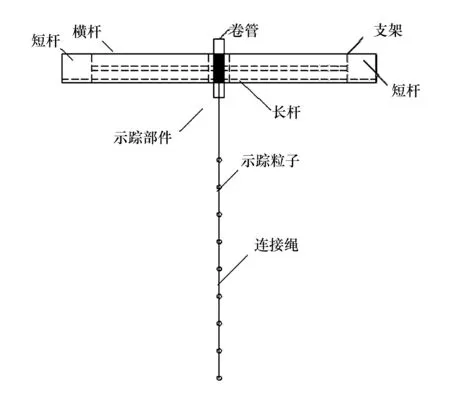
图1 示踪装置结构示意图

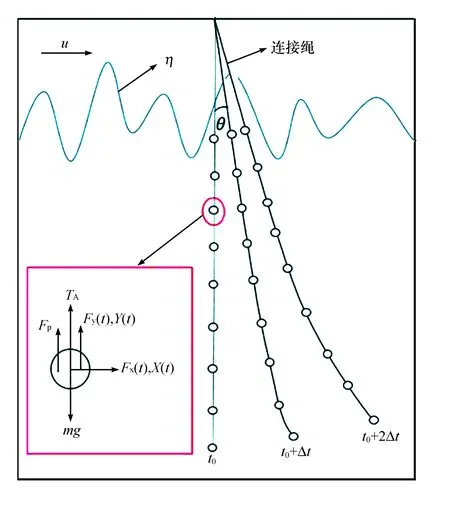
图2 示踪装置受力分析简图

对示踪粒子进行受力分析(见图2),由牛顿第二定律得：

(1)

(2)

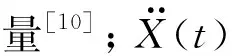
当示踪粒子在流场中做非定常运动时,其所受水体作用力:

Fx(t)=(m+ma)·ax

(3)

Fy(t)=(m+ma)·ay

(4)

式中：ax、ay分别为水质点的水平加速度和竖向加速度。由式(1)—(4)可得：

(5)

(6)

式中TA0=Fp-mg。

随机波浪作用下,水质点水平位移ξ(t)和示踪粒子水平位移X(t)、水质点竖直方向位移ζ(t)和示踪粒子竖直方向位移Y(t)分别表示为

(ξ(t),ζ(t))=Re{(ξ0,ζ0)eiw t},

(X(t),Y(t))=Re{(X0,Y0)eiw t}

式中Re为雷诺数。

示踪粒子连接绳一直处于波浪场中,故连接绳拉力可表示为：TA=Re{T0eiwt}。将连接绳拉力、水质点和示踪粒子位移的随机表达式代入式(5)和式(6)得：

(m+ma)·Re{(-w2ξ0)eiwt}+TAsinθ=

(m+ma)·Re{X0(-w2)eiwt}

(7)

(m+ma)·Re{(-w2ζ0)eiwt}+TAcosθ-TA0=

(m+ma)·Re{Y0(-w2)eiwt}

(8)

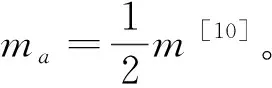
(9)

受力分析表明,当示踪粒子足够小且连接绳足够长时,示踪粒子的水平位移X0与水质点ζ0相等,而竖直位移Y0存在连接绳拉力项,竖直方向上示踪粒子不能准确示踪水质点的运动,这与文献[9]中的实验结果是吻合的。文献[9]中对水质点运动轨迹进行了示踪验证,未对水质点的速度等运动特性进一步研究,很多时候,比较关心的是水质点的水平速度。故本文在受力分析验证该示踪装置有效的前提下,将其引入到实验教学中,并进一步对示踪粒子的水平速度进行实验分析,以探讨该示踪装置的适用范围。

1.2 实验设计

实验在河海大学海岸灾害及防护教育重点实验室的航道实验室的风浪流水槽中开展,其基本尺寸为：长×宽×高=67 m×1 m×1.5 m。

实验水槽的波浪要素率定好之后,将示踪装置固定在水槽中央面,示踪粒子在波浪作用下运动,拍摄其运动视频。实验拍摄采用Canon EOS 5D MarkⅢ高性能数码单镜头反光相机,画面精细度高、实时拍摄清晰度高。拍摄时相机固定在支架上,为避免拍摄时相机抖动,可连以快门线拍摄,同时支架上有能上下升降的螺纹调节装置,可以适应各种实验角度。当摄像机与示踪粒子相距2 m左右时,摄像画面的宽度有1.2 m,能全面覆盖拍摄时间内示踪粒子的运动轨迹。同时,在水槽玻璃板上贴有两根分别和水槽底板平行、垂直的直尺作为坐标基准,用以将实验视频从像素坐标系换算至实际坐标系。实验布置如图3所示。

图3 实验拍摄实物图

2 实验分析

2.1 数据分析步骤

基于摄像机拍摄的实验视频,为获得视频中示踪粒子坐标,现进行如下处理：

(1) 将实验视频分解成30帧/s的照片帧,即Δt=1/30 s,选取适当数量的照片进行分析；

(2) 利用图像处理软件获取照片中示踪粒子的像素坐标,并根据实验放置的直尺将像素坐标按比尺换算得到实际坐标系中的坐标；

(3) 根据坐标和时间差计算出每Δt内示踪粒子的平均速度；

(4) 对算出的示踪粒子的速度-时间序列进行上跨零点求速度振幅；

(5) 微幅波理论水平速度计算可从定点波面序列、理论公式计算和频谱分析3个方面进行。

① 定点波面序列：通过速度势函数Ф将定点波面-时间序列η-t换算得到任一深度处水质点的水平速度-时间序列u-t,同样对其进行上跨零点求得该深度处水质点水平速度振幅[11]。速度势函数为

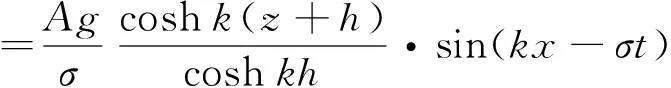
(10)

波面升高为

(11)

水质点水平速度为

(12)

故水质点理论水平速度振幅为

(13)

式中：u为水质点水平分速；A为波浪振幅；k为波数；σ为角频率；h为波浪水深；z为水质点竖向坐标；g为重力加速度；x为水质点水平向坐标；t为波浪传播时间。

② 理论公式计算：可直接将定点波面序列的波高和周期代入公式(13)中计算得到理论水质点水平速度振幅,并与第(4)步中结果对比。

③ 频谱分析：对示踪粒子的速度-时间序列进行快速傅里叶变换得到速度的频域分布,然后求速度频谱的4倍根号零阶矩[12],并与第(4)步中结果对比。以上数据处理均由Matlab编程完成。

2.2 规则波实验结果

规则波实验参数：水深h=0.66 m,波周期T=1.2 s,波高H=0.085 m。示踪粒子至自由波面距离分别设置为：0.36、0.41、0.47 m,此处以-0.36 m处示踪粒子为例。水平方向示踪结果如图4所示。

对示踪粒子的u-t进行上跨零点求得其水平速度振幅：u1=0.09 m/s；

对水质点的u-t进行上跨零点求得其水平速度振幅：u2=0.09 m/s；

将参数代入式(13)计算得到：u3=0.09 m/s。

同样地,可得到所有深度处的示踪粒子水平速度处理结果见图5。

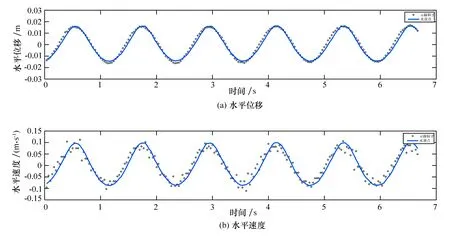
图4 规则波浪作用下示踪粒子与水质点水平方向运动对比(z=0.36 m)

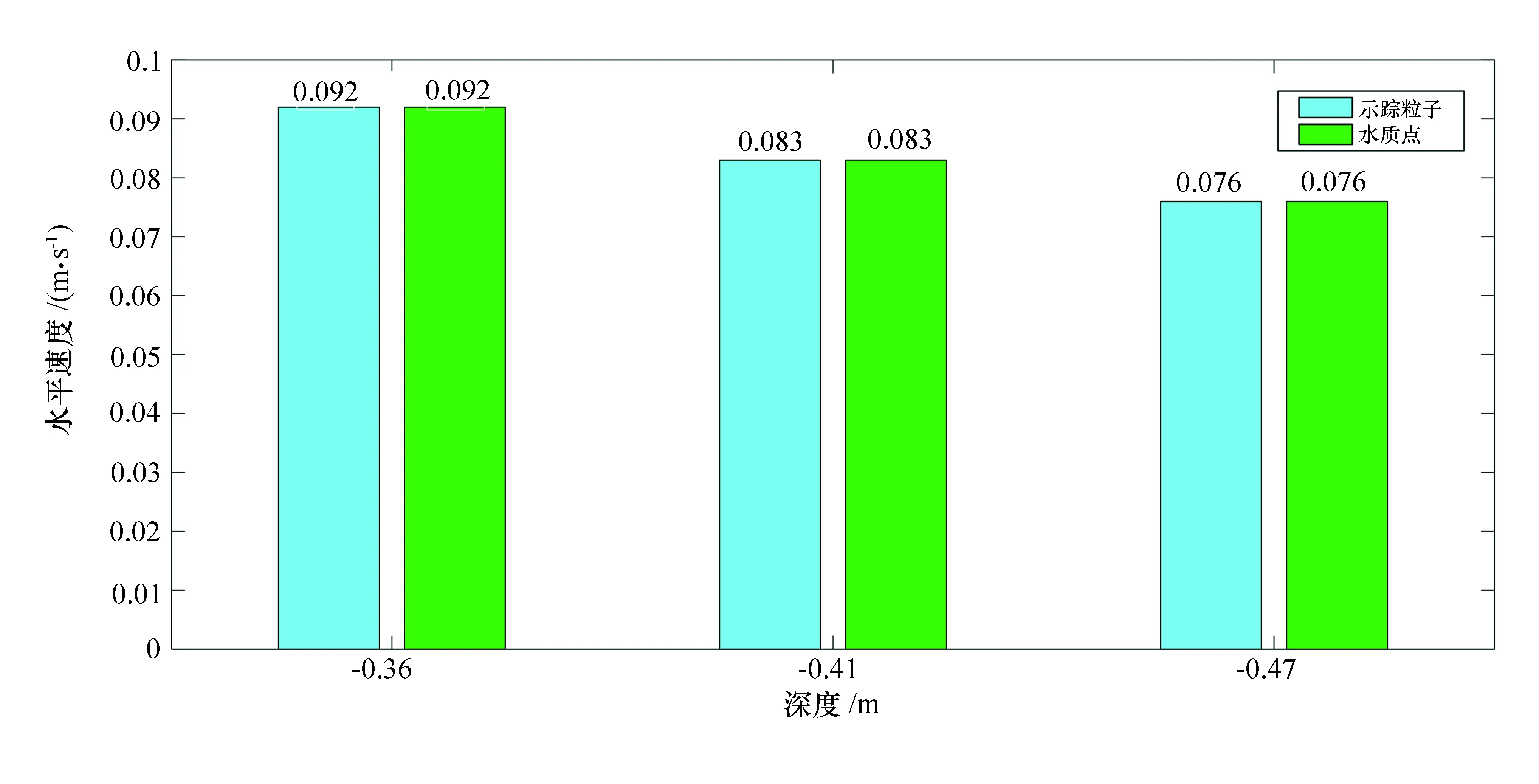
图5 规则波下不同深度处示踪粒子与水质点速度对比

由图5可知,示踪粒子水平速度与微幅波理论公式计算得到的水质点速度在保留3位小数精度时相等,说明示踪装置可用于规则波浪作用下水质点水平速度的示踪实验。

2.3 不规则波实验结果

2.3.1 水平方向位移与速度

不规则波实验采用JONSWAP谱造波,参数：水深h=0.54 m,谱峰周期Tp=3.0 s,有效波高Hs=0.12 m。不规则波主要考虑波表面附近水质点水平速度,示踪粒子至自由波面距离分别设置为0.03、0.08、0.13 m,此处以=-0.03 m处示踪粒子为例。水平方向示踪结果如图6所示。

对示踪粒子的u-t进行上跨零点求得其水平速度振幅：u1=0.25 m/s；

对水质点的u-t进行上跨零点求得其水平速度振幅：u2=0.25 m/s；

将实验参数代入公式(13)计算得到：u3=0.24 m/s；

对示踪粒子的u-t进行FFT得到速度的频域分布Su(f),求得Su(f)的4倍根号零阶矩为：u4=0.26 m/s。

得到所有深度处的示踪粒子水平速度处理结果见图7。由图7可知,示踪粒子水平速度与微幅波理论公式计算得到的水质点速度在保留3位小数精度时相差不大,说明示踪装置可用于不规则波浪作用下水质点水平速度的示踪实验。

2.3.2 不同深度处示踪粒子水平速度之间的关系

依次对3个深度的示踪粒子的6 000个水平速度数据进行函数拟合,将拟合函数与理论比值对比见图8。

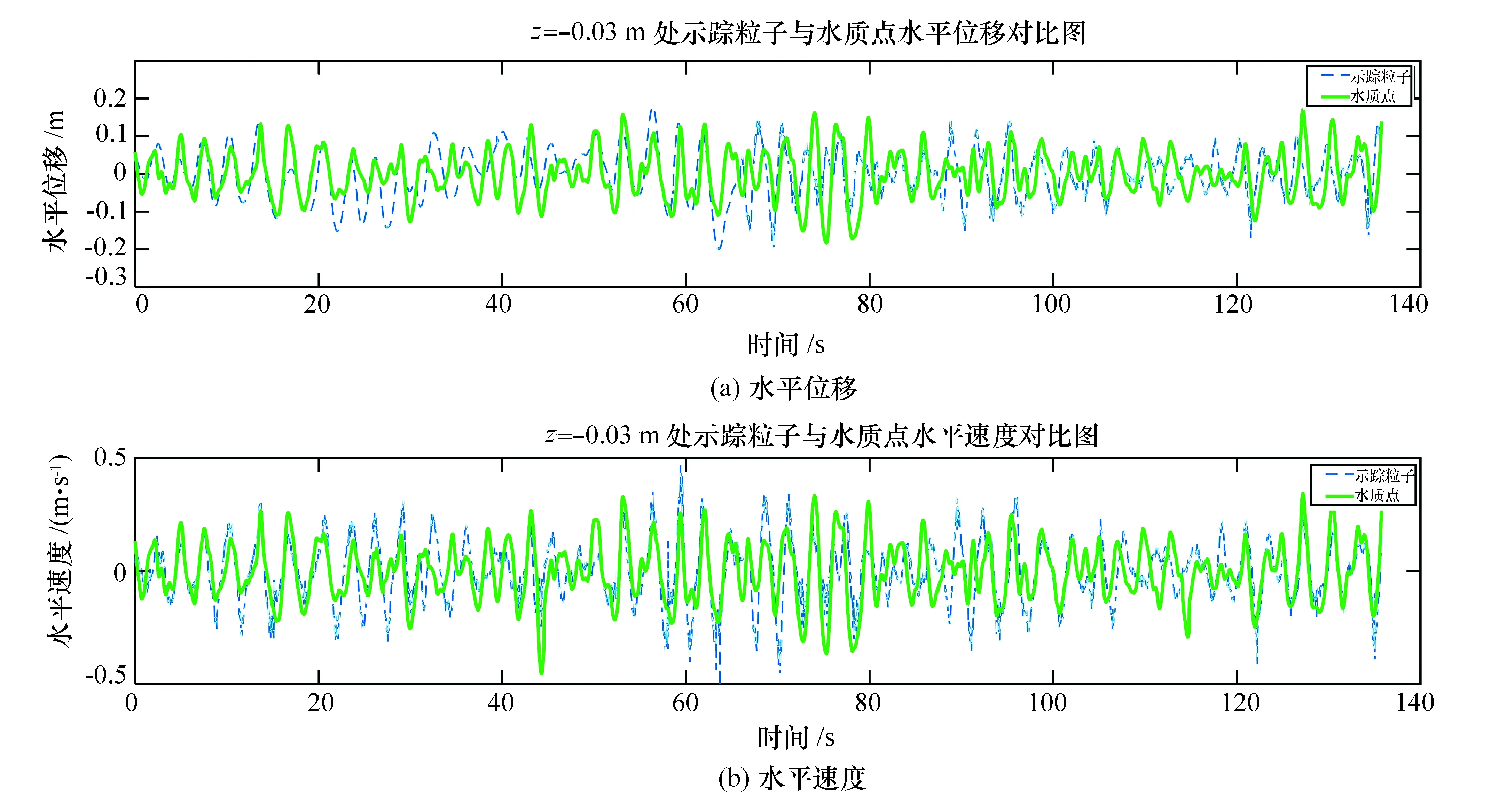
图6 不规则波浪作用下示踪粒子与水质点水平方向运动对比(z=-0.03 m)

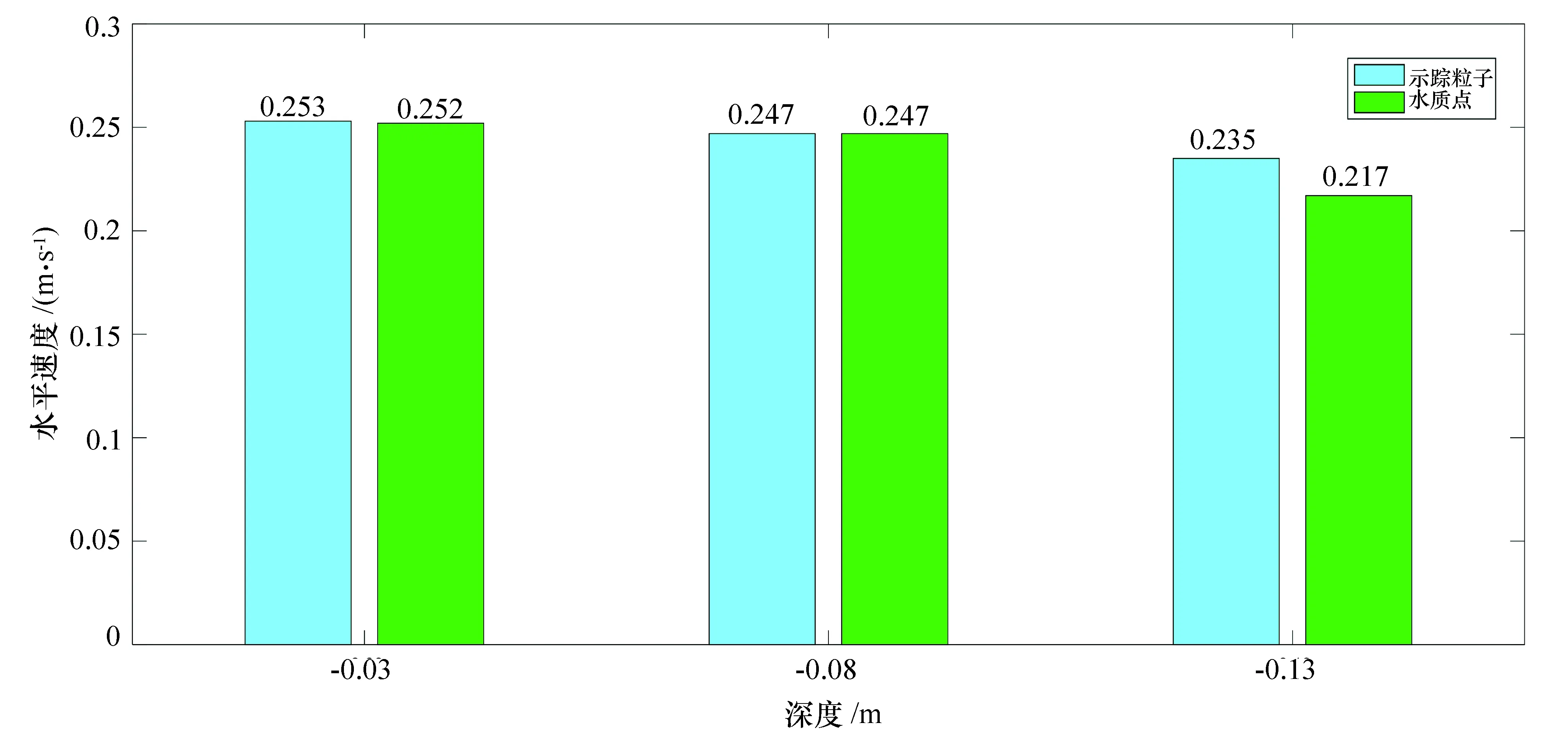
图7 不规则波下不同深度处示踪粒子与水质点速度对比

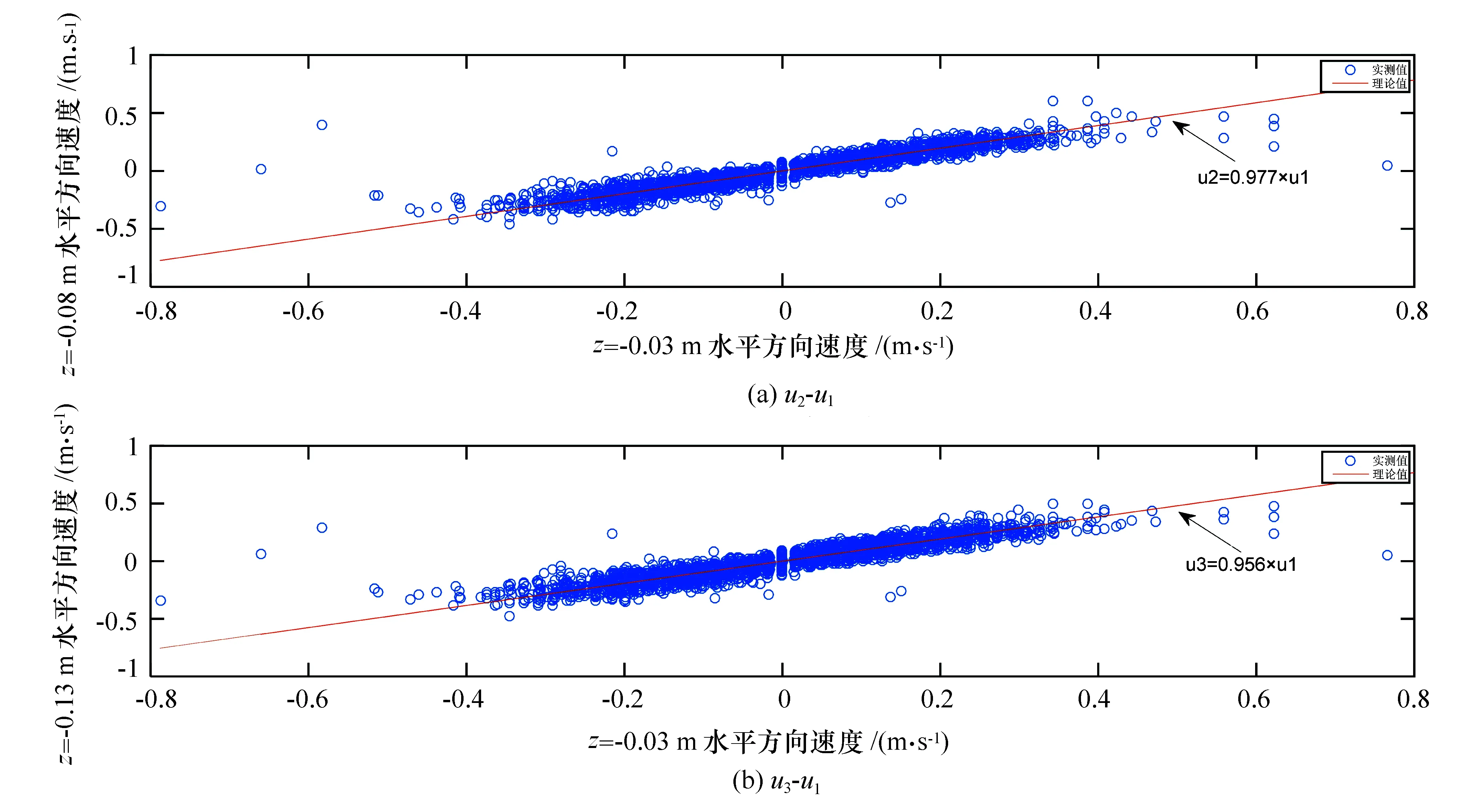
图8 不同深度处示踪粒子水平速度关系与理论值对比

此处u1、u2、u3分别指示踪粒子连接绳上z1=-0.03 m、z2=-0.08 m、z3=-0.13 m处示踪粒子的水平速度,图中实测值为示踪粒子实测速度数据,理论值为根据公式(4)计算得到的与深度有关的比值：

由水平速度关系对比图可知实测值与理论值十分吻合,说明示踪装置对不同深度的水质点可以有效跟踪其水平方向运动,且互不干扰。

3 结语

本实验的示踪装置可使示踪粒子悬浮于流场任意位置,将流场水质点的运动轨迹实时、直观地展示出来,并可做进一步的运动特性分析。通过该实验的学习,学生可掌握水质点示踪技术原理、波浪作用下水质点运动规律以及示踪装置的使用,有利于学生更好地理解和学习波浪理论相关课程。