管理域算法

佘 凤, 曾远柔

(1. 黄冈职业技术学院 计算机系, 湖北 黄冈 438002； 2. 长江工程职业学院 计算机科学系, 湖北 武汉 430074)

分类器中的数据通常与要处理的数据不一样,当标准机器学习提出训练集和测试集来源于相同的数据分布时,许多应用并不赞同此说法,如机器视觉[1]和自然语言处理等。为处理此情况,可使用从源头到目标的转换,提出两种领域间的分布传输,而域自适应法[2-4]中的两种主要类别都是可行的。如文献[5]中显示域自适应法够接触到目标领域中的一些被标记过的例子以及数据。文献[6]通过集中提出统计机器翻译领域自适应问题,并提出解决此类问题的新方法,针对双语网站的识别和定位,提出一种基于全局搜索和局部分类的特定领域双语网站识别方法,实验结果证实,在相同测试集下,特定领域机器翻译系统的性能获得显著提升,验证该方法的有效性。文献[7]中提出一种中间子空间的顺序,此子空间沿着测地线路径连接源子空间和目标子空间。如文献[8]中源数据与目标数据都被输入中间线性子空间中,此空间分布在链接2个原始空间的最短的测地线路径周围。这些子空间的方法虽然有效,成本却很大,且会受到干扰。文献[9]围绕中文分词领域自适应的课题,针对大规模人工分词训练语料难以获得的问题,提出基于主动学习的中文分词方法。文献[10]中通过优化单一线性绘图函数直接将源子集与目标子集连接起来。此方法不仅被证明比最新的其他方法要好,而且在闭合形式下也是可计算的。

文献[10]面临着两个主要的问题。首先,文献[11]方法指出两种分布间的传输能通过线性传输得以纠正,但这很容易被许多现实世界的应用所推翻;其次,此方法指出在实行、适应时,需要所有的源案例及目标案例,然而在大多数情况下,只有一个源数据的子集会与目标域分布相似,反之亦然。为此,本文将用以下方式处理这2个问题：一是从两种域中选取界标来减少源分布与目标分布的不一致性；二是使用关于界标选取的高斯核函数将源数据与目标数据输入共享空间中,这使得从数据库中捕捉到非线性变得容易；三是提出一个线性绘图函数将源子空间与目标子空间连接起来,这只需要简单地计算出源维度数量与目标维度数量之间的内积。通过实验证明该方法优于当前的域自适应法。

1 自适应法拟定域

自适应法拟定的域是针对域自适应的以界标为基础的子空间对接法,是完全无人监督的,因此在执行域自适应时,不需要任何标注。从源域中获取的被标注部分只用于随后提出分类器。

源数据(S)和目标数据(T)被认为是分别从源分布DS和目标分布DT中获取而来。域自适应指出,源分布与目标分布是不一样的,但它们也有一些相似之处,这使得将在源域中提出所得放入目标域中成为可能。不一样的是,若有一套LS的源案例,它们就能用于提出适合目标域的分类器。

通过下述方法将两种观点结合起来。首先,将源案例与目标案例输入到有关选取好的界标的普通子空间中。接着,在两种域中运行子空间对齐。在S和T中选取出界标后,使用高斯核将其所有的点输入到界标中,用KS和KT重新展现源点与目标点,并通过子空间对齐法完成映射。

与文献[11]相比,通过两步法在捕捉非线性时,既保持准确性,操作又简单快捷。接着通过仔细分析从多尺度界标选取到子空间对齐和分类方法中的每一个步骤。

2 设定多尺度界标及核投影

本文方法的第一步就是选取一些点作为界标。直观来看,一套好的界标能将源数据与目标数据输入到共享空间中,使得它们的分布更加相似。该方法从S和T中选取界标且未使用过任何其他标记。界标选取最终输出：A={α1,α2,...},其中A⊂S∪T,为避免昂贵的重复优化法,通过提出一种直接法,其能判断是否该保留某个点作为界标。

2.1 设定界标

事实中,通过界标选取法把从特征选取(S∪T)的每一个c点都当作备选界标,并独立提出每一个备选界标。对备选界标执行质量检测,若检测高于阈值,就将其设定为界标。为评估备选c的质量,首先要用高斯分布的标准误差s,计算其与p∈S∪T所有点的相似性,界标K(c,p)公式如下：

(1)

式中p为核基半径。

计算备选界标c的质量来作为源点与目标点中K值分布的重复。因此,在使用核基以后,若源点与目标点的分布是相似的,那它就是一个好界标。

2.2 分析多尺度捕捉数据属性

式(1)中的核基半径p值很重要,因其设定备选界标中相邻界标的大小,为给定的界标选取准确的s值,且能在准确范围内捕捉到本地现象,并更好地将源分布与目标分布对齐。由于s的极端值会将源点分配的目标点完美地匹配起来：K值会变成0(当s接近0的时候)或1(当s非常大时),故应当避免。

计算备选界标的质量事实中是做一个多尺度分析：通过选取最佳的s来捕捉数据的本地属性,同时避免s的极端值。为达到这个目的,通过计算所有元素对中欧几里得距离的分布,并尝试分布的每一个百分位数。有这个以百分位数为基础的方法,通过尝试一串s值,其结果貌似都是可信的。通过计算s中源分布和目标分布之间的重复,保留备选界标中质量检测最佳的一个。

2.3 重复标准分布

对于备选界标c和标尺(标准误差)s,通过计算出2个K值集中的重复度：源点中的KVS和目标点中的KVT。为降低计算成本,两种分布都被近似为普通分布,并用标准误差公式实施总结：μS,σS,μT,σT。为能使用固定阈值并对其赋予意义,通过采用一种标准重复计算法以下：

(2)

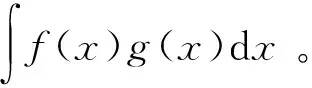
(3)

(2)中的分母与给定σsum(由μS=μT中获得)中分子的最大值一致。分母作为一种归一元素,当分布完美匹配且给出更简单的解释时,将重复设定为1,有助于阈值th的选取。

2.4 设定界标投影

S∪T中的每一个核基半径素p都通过使用有着标准误差的高斯核基被投影到界标αj∈A中,

(4)

整体来看,S和T中所有元素都被投影到普通空间内。由于有界标,这些普通空间有许多维度。仿照其他非线性法,通过在随机从S∪T中提取的要素对间将σ设定置成中间距离。也通过一些交叉验证选取σ的值。在投影以后,最终获得源与目标的新代表,分别是KS和KT。

2.5 对齐子空间

在采用非线性投影集KS和KT后,实施子空间对齐法。主成分分析(PCA)分别用于域中,提取拥有最大子空间维度数量的d子空间维度数量。根据文献[11]中的理论,能设定d的最佳值,因文献[11]中提出一个基于标准集中不平等的关于维度数量的一致性定理,其可以在2个连续维度数量的误差中找到界限。通过利用此界限有效地调整主成分分析中的子空间维度数量d。源域和目标域中的d子空间维度数量分别由XS和XT表示。域中的每个要素都能分别被投影到其子空间KSXS和KTXT中。

子空间对齐的目的是找到线性转换M,M能将源子空间维度数量最好地投影到目标子空间维度数量中。此外,通过找到M来减小源维度数量和目标维度数量之间欧几里得距离的数量。此减少等同于下列弗罗宾尼斯范数：

(5)

对齐转化M将要素从源特征空间中映射到目标特征空间,其能通过计算KSXSM,将投影好的源要素KSXS作为投影好的目标要素KTXT带到相同的特征空间中。此算法是以选取的界标为基础的子空间对齐(LSSA),其伪代码见如下算法:

算法1：LSSA：以界标选取为基础的子空间对齐和分类

要求：S,T,源标记Ls, th,子空间维度d。

保证：Lt是T中要素的预估标记

A←choose_landmarks(S,T,th)

σ←median_distance(S∪T)

KS←project_using_kernel(S,A,σ)

KT←project_using_kernel(T,A,σ)

XS←PCA(KS,d)

XT←PCA(KT,d)

PS←KSXSM

PT←KTXT

classifier←learn_classifier(PS,LS)

LT←classifier(pT)

3 实验与结论

本文实验目的：第一,提出界标选取法的表现,即是处理与其他界标选取法相比较而言的无人管理的图像域自适应；第二,希望证明在与子空间对齐法联合使用时,此法在自适应领域有巨大的提升,包括文献[10-11]中描述的最好、最新的方法。

3.1 实验与数据集设定

本文在图像域自适应的标准数据集中实施实验。通过所使用的办公数据集[12]包括从摄像头中获取的图像(用W表示),从数字SLR相机中取得的图像(用D表示)和从百度中取得的图像(用A表示)。此外,还运用一些大学实验图像[8](用C表示)。每一个数据集都为10种类别提供不一样的图像。因此,通过能从4个数据集(A,C,D,W)中获取到12种域自适应子问题。其中一个数据集扮演源S的角色,而另一个被看作是目标T。本文通过符号S→T证实一个域自适应问题。目的是从被标注的源S中提出一个SVM分类器(使用SVM的线性核基),并将其配置到目标T上。根据参考文献[7-8,10, 12]中的标准协议得到源案例和目标案例。

界标选取法的比较：为完成这个实验,通过将该方法(表1中的MLS)域下列3中基线实施比较。

随机选取：通过随机选出500个界标(每个域中250个),并重复5次,得到一个平均表现。

无界标选取：通过将所有源案例与目标案例作为界标。

所有的备选界标都采用相同的标准误差σ。σ被设定为最标准的误差(对此条基线有利),这有助于获取两种分布之间最大重复的平均值[13]。对于MLS和σ-LS,本文将重复率固定为0.3来选取界标。由于规范化,0.3的阈值等同于30%的重复率。本文还将MLS域其他界标选取法实施比较,即用界标连接点法(CDL)。测地线流内核(GFK)[8]中中间子空间的顺序分布在连接源域与目标域的测地线路径两旁。一步子空间对齐法(SA)方法经过提出2个子空间的线性转化而提出。文献[12]中提到的转化联结匹配法(TJM)，此方法是基于特征匹配和案例权重的最近提出的方法。

此外,本文在两种基线下实施实验。第一种并没有实施任何的自适应(NA)；第二种在源域和目标域中实行2个独立的KPCA,并用SA算法(用KPCA+SA表示)提出线性转化。

3.2 分析结果

表1中RD 、ALL、σ-LS 、CDL、 MLS分别表示无人管理自适应法的5种界标。做出如下结论：首先,平均来说,本文的方法(使用学生成对测试)大大优于其他方法(平均精确度Avg为48.1%)，在12个域自适应任务中,MLS在8个子问题中的精准度都是最佳的；其次,对于两种子问题(W→D和D→W),ALL更好些。这意味着将所有源案例和目标案例保留在这两种对称情形中比试图寻找界标要好些。值得一提的是[14],这两种子问题都是最简单的问题,它们有着最高的精准度,证明保留所有数据的好处。此外,通过的方法在12中问题中的10种中都比CDL有优势,而且CDL在半无人管理的域自适应情境中是专门选取界标的。最后,单一尺度法(采用固定σ)并不是很好。这证实在MLS中,为每一个界标选取最好的活动半径是多么重要。为MLS为每一个域自适应子问题选取出界标的分布。这证实即使没有类别信息,本文的方法仍然能在各种类别中做出平衡选取。

表1 关于12个无人管理的域自适应子问题的5种界标选取法的比较

与当前最新的无人管理自适应法作比较。表2给出最新的无人管理子空间对齐域自适应法的实验结果。值得注意的是,本文的LSSA法在12种中的7种子问题上都比其他方法表现好,同时TJM在剩下的5中方法中表现更好。然而,平均来看,LSSA大大优于TJM(52.6%对50.5%)。此外,TJM的时间复杂性远远大于其他方法,因其需要解决一个不小的优化问题,而本文的方法包含的针对界标选取的贪心策略和针对子空间对齐封闭解更加有效。TJM和LSSA的精准度的差别在于,前者采用权重机制,主要能将两种域移动得更近一些,而后者通过高斯假设定,同时考虑到方式及界标数据分布的标准误差。从表2中可以看到,LSSA远远优于SA,LSSA能捕捉到非线性,这是SA难以与其比较的。然而,考虑非线性的方式也是一个关键。的确,正如KPCA+SA所表示的那样,在子空间对齐之前执行2个独立的KPCA会导致最坏的结果。

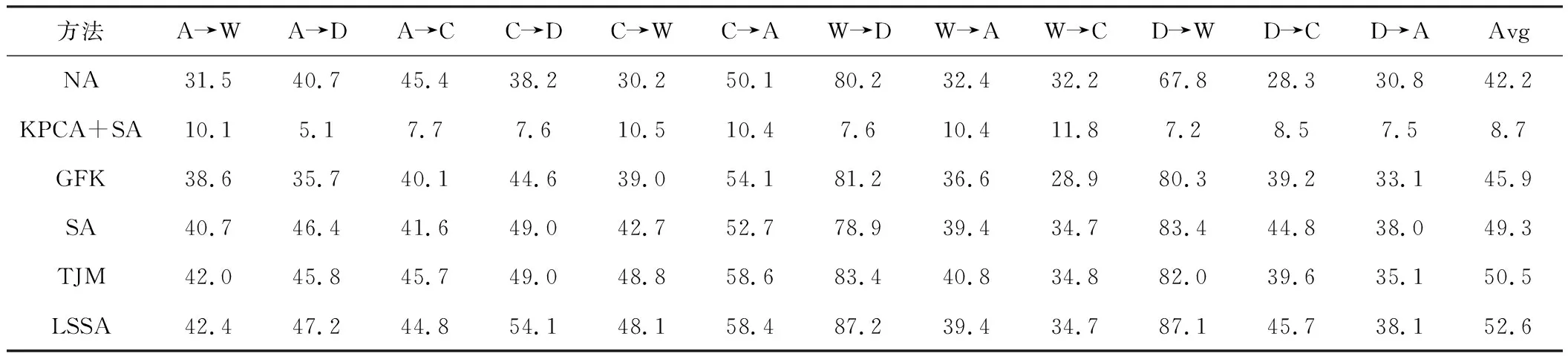
表2 无监督方法的比较

4 结语

首先,从源S和目标T中选取界标将源分布与目标分布间的映射最大化；然后,在选取好的界标上应用高斯核,以得到新的源点(KS)与新的目标点(KT)；接着,在执行有关维度数量的子空间对齐之前,实行2个独立的PCA；最后,从被标注的源数据中提出分类器,并将其执行到目标域中。在图像域自适应的大量实验证实：所提方法选取出的界标能降低领域之间的不一致性,用于非线性项目,能呈现出有效子空间对齐的数据,优于其他无人管理域自适应算法。