基于正交试验的旅客登机关键因素仿真分析

任新惠,徐小冰

(中国民航大学 经济与管理学院, 天津 300300)

在20世纪90年代,200名航空旅客的登机时间约为22 min[1],而2009年苏黎世机场的调查发现,该时间已增加至40 min,且登机时间在短途航线中占到了总旅行时间的40%～60%[2]。研究登机问题、缩短登机时间,对航空公司、机场和乘客都有重要意义[3-4]。

目前,对航空旅客登机问题的研究主要是用仿真方法比较登机策略和各因素对登机时间的影响[5-6],运用数学或物理方法建模求解最小登机时间[7-8],以及对登机策略进行改进优化[9-12]。其中对登机时间影响因素的研究侧重于两方面：

一是根据旅客登机数据建立离散登机仿真模型,比较客座率、行李、登机策略和登机口数量对登机时间的影响，对旅客属性和登机策略的稳健性进行研究。例如迟到/提前登机旅客、坐错位置旅客、团体旅客、不同旅客的行走速度和超越座位的可能性等[5-6]。

二是针对某个影响因素进行登机方式的优化改进，例如旅客携带行李数量以及放置行李问题。Steffen[4]利用马尔可夫-蒙特卡洛优化算法提高了不同旅客处理行李的并行性,提出“Steffen策略”。文献[11-12]提出行李均匀分布在机舱内的座位预分配算法、多行李优先登机的策略、基于干扰转移的登机策略等。

此外，航空旅客的个人特征和属性被关注。Tang等[9]首次提出根据旅客个体特征(年龄,移动速度,行李重量等)来安排登机顺序的新方法；Notomista等[10]利用图像识别技术快速检测乘客的体型以及携带行李的大小,并根据视频处理结果提出座位分配算法；以团体旅客为研究对象提出动态优化登机模型[13]。

本文通过对登机影响因素的分析,得到解释结构模型,运用正交试验方法和仿真软件对航空旅客登机问题进行研究,对正交试验结果进行极差分析和方差分析,得到旅客登机影响因素的主次顺序和显著水平。

1 基于ISM的旅客登机影响因素分析

1.1 旅客登机影响因素的确定

旅客登机问题的研究涵盖旅客从登机口到入座的所有决定和活动,包括登机策略的选择和实施、登机通知、携带行李、登机口排队、检票、步行、行李放置和入座[3]的全过程。将旅客登机影响因素分为机场、飞机、旅客和航空公司4方面,如表1所示。

运用解释结构模型分析旅客登机影响因素的目的,一是探究这些因素的相互关系,二是为了确定仿真实验中选取的因素。由于机舱门开放数量、旅客迟到/早到等在正交试验中不易操作,因此,确定建立影响旅客登机的解释结构模型包括登机区、廊桥、放行间隔、排距、过道宽度、座位布局、客座率、行李舱、行进速度、旅客年龄、行李、登机策略这12个因素,记为

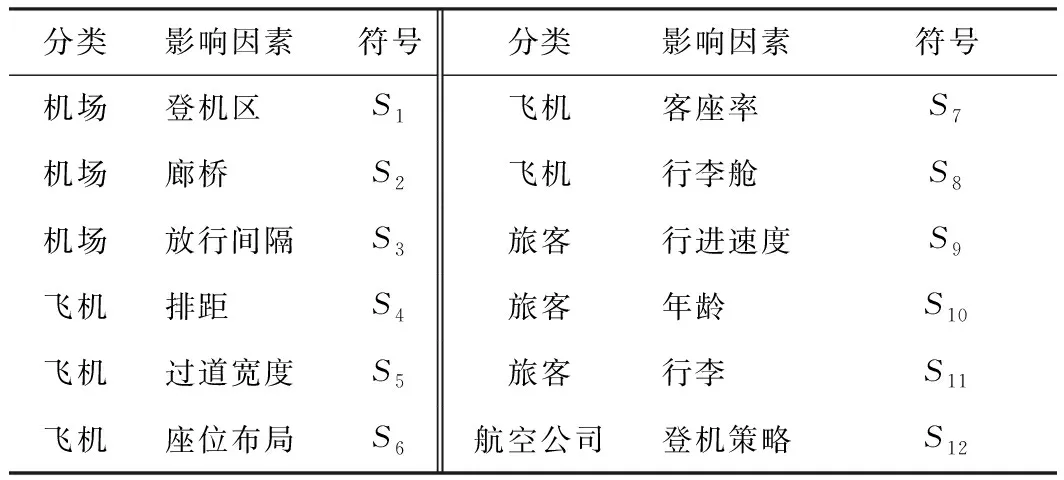
S={Si|i=1,2,3,…，12}

1.2 构建邻接矩阵

根据旅客登机影响因素的相互关系,构建了邻接矩阵A,其中S={Si|i=1,2,3,…，12}分别表示12个影响因素,另外S13表示旅客登机过程。在该矩阵中,元素aij表示因素Si和因素Sj之间的直接关系,即：

(1)

1.3 建立可达矩阵及关系划分

通过布尔运算法则,可根据邻接矩阵A求得可达矩阵M,其计算公式为：

M=(A+I)r

(2)

可达矩阵M中的αij=1,表示元素Si到Sj间存在可达路径,即要素间的直接或间接关系。若αij=0,表示元素Si到Sj间无影响关系。

在可达矩阵的基础上,整理每个要素的可达集R(Si)、先行集A(Si)、共同集C(Si),并进行级位划分,级位划分结果为：L1={S13},L2={S1,S2,S3,S4,S5,S6,S7,S9,S12},L3={S8,S10,S11}。

1.4 提取骨架矩阵并绘制有向图

对可达矩阵做缩减梳理,合并矩阵中的强连接要素集合,剔除具有邻接二元关系的要素间的越级二元关系以及自身到达的二元关系,得到骨架矩阵,并根据骨架矩阵得到旅客登机的解释结构模型,如图1所示。

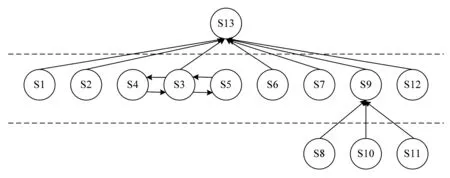
图1 旅客登机影响因素的解释结构模型

2 基于正交试验的旅客登机仿真实验设计

2.1 正交试验设计

正交试验是一种安排多因素、多水平的优化试验方法。正交试验方法包括因素、水平、试验指标、关键因素等要素。因素是指影响正交试验指标的要素。因素所处的状态为水平、因素水平的变化会引起试验指标的变化；关键因素是指对试验指标影响最大的因素。正交试验具有两个特点：(1)每个因素的不同水平都出现了同样的次数,称为“均衡分散性”；(2)正交试验能排除其他因素的干扰,对某个因素的不同水平进行比较,称作“整齐可比性”。本文运用正交试验方法研究旅客登机问题,通过安排较少次数试验,得到试验数据,并分析旅客登机的关键因素。

2.2 仿真实验的因素选取及水平确定

通过运用解释结构模型对旅客登机影响因素的分析，得到层次结构模型。从图1可以看出：深层次因素是行李舱、旅客年龄、行李。仿真因素的选取从层级结构图每个分支的底层因素开始,同时考虑仿真实验条件和现实中实际状况进行判断。若该因素适合仿真实验条件,同时满足正交试验要求,则该分支要素选取结束；若不合适,则对该元素的上层因素进行判断,直到确定了该分支影响因素或该分支没有合适的仿真实验因素。

正交试验条件中剔除了登机区、廊桥、座椅布局、排距、过道宽度、行李舱等不可变的因素。对于放行间隔、客座率、行进速度、旅客年龄、行李和登机策略这6个可变因素,考虑到旅客年龄和行李为行进速度的底层因素,因此仿真实验中选取旅客年龄和行李。由于客座率越高,登机时间越长,而本文侧重于研究满座情况下其他因素的影响,因此在仿真实验中假设客座率为100%。最终,确定了仿真实验的4个因素分别为A——放行间隔S3、B——旅客年龄S10、C——行李S11、D——登机策略S12。

放行间隔又称为旅客登机频率,旅客登机频率会影响总登机时间。为了合理地确立仿真实验中的放行间隔水平,Giitsidis运用元胞自动机建模旅客登机过程，并仿真12种放行间隔[6],文献[14]用元胞自动机仿真11种放行间隔。以上研究表明：当放行间隔较小时(1～3 s/人),不同的登机策略存在明显的差异,同一策略的登机时间没有明显差异；当放行间隔达到6 s/人时,策略间的差距几乎消失[12]。本文在前人研究基础上选取3个放行间隔水平——2 s/人、4 s/人和6 s/人。

登机策略甚至决定了旅客登机的顺序,登机策略研究的核心是通过优选登机策略以减少登机时间[5-6]。除去开放式/自由登机策略,预先指定座位的登机策略分为随机登机、按组登机和按座位登机3类。Steffen策略是效率最高的策略,近年来有很多在Steffen策略的基础上进行优化改进的新登机策略[10-11]；Random策略是采用广泛的一种登机策略；Back-Front(BF)策略是按组登机中最易于实施的登机策略。本文采用这3种登机策略进行仿真实验。

行李的数量和种类会影响旅客放置行李的时间,对登机时间有重要影响。根据文献[14]给出典型行李分布值,携带0、1、2件行李的旅客比例分别为20%、60%、20%。将行李分类为小包、背包和拉杆箱,并将旅客携带的行李细化为无行李、小包、背包、拉杆箱、小包和背包、小包和拉杆箱、背包和拉杆箱等7种情况。根据相关文献和天津、昆明、西安、成都等机场共20个航班旅客携带行李情况,本文选取3种行李水平并用F(few)、S(standard)、M(much)表示,如表2所示。

表2 3种行李分布

年龄作为旅客个人属性的一部分,会影响旅客在机舱内的行进速度。Tang等[9]在行人流理论的基础上提出了根据乘客个体特征(旅客年龄、移动速度、行李重量等)来安排登机顺序的方法。本文按照旅客年龄分为青年旅客和中年旅客两类(忽略年龄过小、过大以及特殊旅客),设置青年旅客分别占30%、50%和70%。

根据上述4个试验因素及其取值,得到仿真实验因素和水平表,如表3所示。

表3 试验因素和水平表

2.3 仿真实验的指标选取

实验指标必须能够客观评价实验对象的特定性质,并且具有代表性。旅客登机时间反映了登机的效率,干扰次数反映了登机过程中的干扰情况。

2.3.1 登机时间

登机时间是指第一名旅客进入机舱开始到最后一名旅客完成入座所经过的时间。Steffen和Hotchkiss[15]在试验中测量2个登机时间：(1)第一名旅客进入机舱到最后一名旅客完成入座的“官方登机时间(official time)”；(2)通知旅客登机到最后一名旅客完成入座的“延伸登机时间(extended time)”。本文选取的实验指标为前者,其计算公式如下：

Tboarding=Tend-Tenter

(3)

其中：Tboarding为登机时间；Tend为最后一名旅客完成入座结束时间；Tenter为第一名旅客进入机舱时间。

2.3.2 干扰次数

登机干扰是指旅客登机过程中受到阻碍而无法到达座位,必须停下等待正在放置行李或入座的其他旅客,主要分为座位干扰和通道干扰。座位干扰是指中间或靠窗座位旅客晚于外侧旅客登机时,先登机的旅客需要起身相让；通道干扰是指通道中有旅客正在放置行李或有旅客在让座而影响其他旅客通行和入座的情况。多数学者认为减少登机干扰的数量就能减少登机时间[7-8]。干扰次数的计算公式如下：

Ninterference=Nseat+Naisle

(4)

其中：Ninterference为干扰次数；Nseat为座位干扰次数；Naisle为过道干扰次数。

2.4 构建正交试验方案表

采用4因素、3水平的正交试验,正交表记为LM(QN)=L9(34),其中L代表正交表,M表示要做M次试验,QN表示有N个因素,每个因素有Q个水平,如表4所示。

表4 旅客登机正交试验方案设计

3 旅客登机仿真实验

3.1 旅客登机行为的建模仿真

元胞自动机将空间划分为有限的网格,网格中格点代表单个旅客,所有格点遵循相同的局部规律、作出同步更新,是在离散的时间维度上演化的动态系统。为了建模和仿真旅客登机过程、得到不同试验指标,确定影响因素对实验结果影响的主次顺序和显著程度。本文针对A320机型,设计25排6座的元胞自动机模型仿真旅客登机行为。按照旅客登机正交试验方案安排仿真实验,并在正交表中记录试验结果。

3.2 仿真实验结果的数据分析

利用元胞自动机仿真软件对9组仿真实验进行建模和仿真,得到对应的试验指标的仿真结果(见表5)。

表5 正交试验结果

选用极差和方差两种方法分析正交试验结果。

3.2.1 极差分析

为了分清试验各因素的主次顺序,判断试验的因素最佳水平组合,分别对登机时间和干扰次数2组试验指标进行极差分析(见表6)。其中Kjm为第j列因素、m水平对应的试验指标和；kjm为Kjm的平均值,该指标可以判断第j列因素的最佳水平组合；Rj为第j列因素的极差,Rj=max(Kjm)-min(Kjm),反映了第j列因素水平波动时,对应的试验指标的变化幅度。Rj值越大,说明该因素对相应的试验指标的影响越大,极差最大的因素也就是最主要的因素。Rj值越小,说明该因素在所选用的范围内变化时,对该指标影响不大。根据Rj的大小能够判断试验因素的主次顺序。

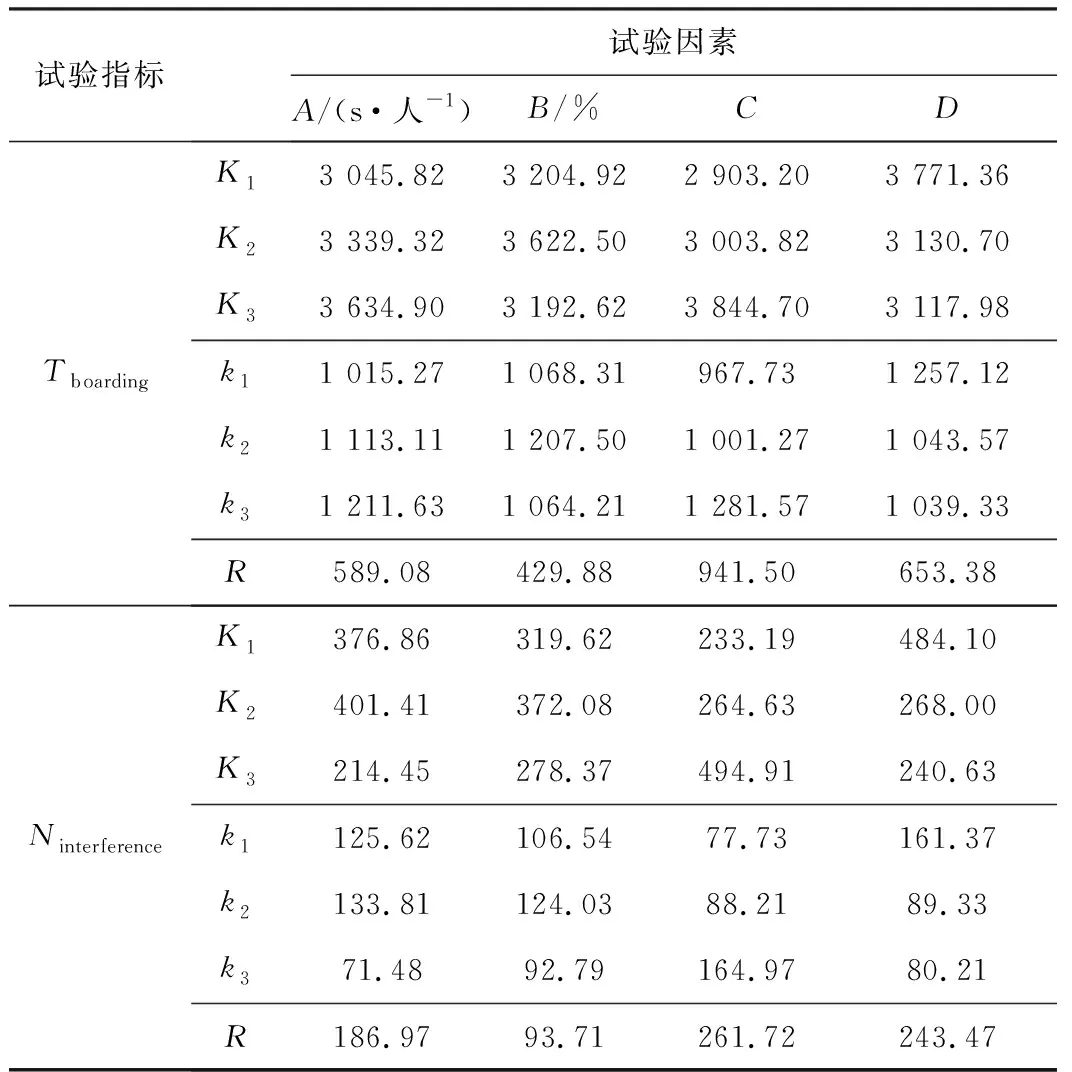
表6 试验指标极差分析

从表6可以看出,登机时间和干扰次数受4个因素的影响,有着相似的规律。行李均为最主要因素,其次是登机策略和放行间隔,旅客年龄对它们的影响最弱。另外,登机时间的最佳水平组合为C1D3A1B3,干扰次数的最佳水平组合为C1D3A3B3。对比两者的最佳水平组合发现,行李、登机策略和年龄的最优取值是相同的。对于放行间隔来说,两者的最优水平存在差别。从表5可以看出,登机时间随放行间隔的增加而增加,这与Giitsidis[6]的研究结果相同。另外,当放行间隔从2 s/人增加到4 s/人时,干扰次数有细微差异；当放行间隔增加到6 s/人时,干扰次数明显减少。

3.2.2 方差分析

为了区分正交试验中试验因素对试验结果的影响,对试验结果进行方差分析,运用SPSS软件输出主效应方差分析表,其中各个因素的显著性P值见表7。

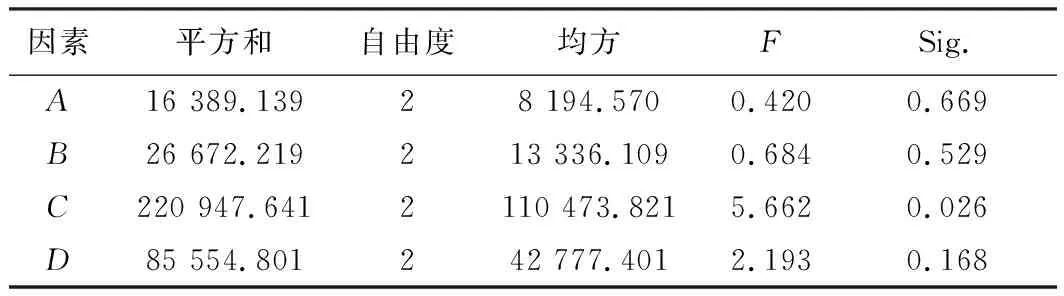
表7 各因素的显著性P值

在95%的置信水平下,行李对登机时间和干扰次数的影响最为显著,其次是登机策略,旅客年龄和放行间隔为不显著因素。通过方差分析得出的因素的重要程度排序与极差分析一致。

4 结论

通过对航空旅客登机的4因素、3水平的正交试验仿真,得出以下结论：

(1) 采用极差分析法分析了各因素的主次顺序,得到因素的重要程度依次为行李、登机策略、放行间隔和旅客年龄。

(2) 采用方差分析法得出各因素的显著水平,结论是行李为影响最显著因素,其次是登机策略，放行间隔和旅客年龄为不显著因素。

借鉴仿真实验的结果，有助于设计新登机策略、提高旅客登机效率。