基于粒子群算法优化PIDNN的温室系统解耦控制

王 鹏， 龚瑞昆

(华北理工大学电气工程学院，河北唐山 063210)

温室系统是一个复杂的多变量系统，具有时变性、时滞性、非线性等特点，且多种变量之间有着相互耦合的关系。随着社会的发展，对温室控制的要求也逐渐提高，但是对于温室系统的研究还处于基础阶段，大量应用于工业的技术并没有在农业中得到应用，使得温室系统的控制无法跟上当前技术发展的水平。目前，对于温室的控制研究主要集中在对温室中某一单一变量的精确控制上，如雷勇等主要通过运用新的智能算法优化对温室系统的温度进行控制，使温度这一大惯性、非线性变量的控制精度和稳定性有所提高，对植物生长环境的优化改进发挥了有利影响[1-3]。季宇寒等针对温室中的CO2浓度进行研究，通过调节温室中CO2的施用量，使CO2浓度维持在作物需求的合理范围，从而增加温室作物的产量[4-6]。朱舟等着重研究了光照度对温室作物生长的影响，通过建立温室补光模型，合理调控温室的光照需求[7-8]。温室系统是一个多变量耦合系统，温度、湿度、CO2浓度、光照度等变量之间相互耦合，某一变量的变动就会对其他变量造成影响，所以针对单一变量控制的研究，无法同时满足变量之间的协调控制，文献[9-10]分别通过模糊控制和基于改进遗传算法的模糊神经网络对温湿度进行解耦控制研究。为了解决温室温湿度耦合问题，本研究提出基于粒子群优化(PSO)算法的比例-积分-微分神经元网络PIDNN，温室系统解耦控制方法。

1 PID神经元网络原理

1.1 PID神经网络简介

比例-积分-微分(PID)神经元网络不是单纯地将PID与神经网络相结合，而是通过将PID的控制规律与神经网络的优点相结合，形成的一种新型改进神经元网络。它既具有常规PID控制器控制规律简单易用的优点，同时又具有神经网络非线性映射能力，舒怀林对PID神经元网络(PIDNN)进行了详细描述[11]。

1.2 多输出PID神经元网络的结构

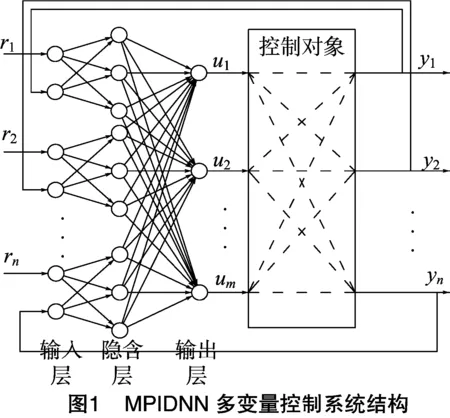
考虑到研究对象是多输入多输出系统，所以选用多输出PID神经元网络(MPIDNN)，其为2n×3n×m形式的网络(图1)，可见针对m输入n输出的控制对象，采用n个单输出PID神经元网络(SPIDNN)单元，输入层有2n个输入节点，每个子网输入某一单变量的给定值和控制对象输出值，通过隐含层动态运算，汇聚到输出层中，输出层有m个节点，通过控制研究对象的控制输入，使研究对象达到控制要求。

1.3 多变量PID神经元网络算法分析

1.3.1 输入层计算 输入层的神经元数为2n个，各神经元结构相同，因此每个神经元的输入输出相等，即

(1)

式中：rn(k)表示控制系统的输入目标值；yn(k)表示控制系统的输出值；netni(k)表示输入层第i个神经元的输入值总和，i表示子网络中输入层序号(i=1，2)；n表示第n个子网络的序号；k为迭代次数。

神经元的状态为

uni(k)=netni(k)。

(2)

式中：uni(k)表示第n个子网络中输入层第i个神经元的状态。

由此可得，输入层神经元的输出

(3)

式中：xni(k)表示第n个子网络中输入层第i个神经元的的输出值。

1.3.2 隐含层计算 隐含层各神经元的总输入为

(4)

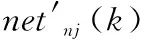
隐含层不同于输入层，每个子网络的隐含层都由3种不同的神经元组成，这3种神经元结合PID的控制规律，将PID的比例运算、积分运算和微分运算规律按照神经元网络的转换规则融入到神经元中，其转换后的形式既保留了PID的特性，又包含了神经网络的动态优化特点，这3种神经元状态分别为

比例元：

(5)

积分元：

(6)

微分元：

(7)

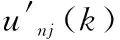
隐含层各神经元的输出相同，其形式为

(8)

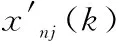
1.3.3 输出层计算 针对n输入m输出的PIDNN控制器，输出层共有m个神经元，通过隐含层输出值以及隐含层和输出层之间的权值运算，可得各输出层神经元总输入为

(9)

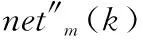
输出神经元的状态表示为

(10)

输出层各神经元的输出值，也是系统所须控制的控制对象的控制输入值，两者之间是等价的关系，表示为

(11)

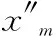
1.3.4 目标函数的计算 PID神经元网络控制的目标是使控制对象的输出值根据目标值变动，并尽可能的接近目标值，PIDNN控制器达到目标的途径就是使各神经元间的权值最合适，且使控制量和目标值的差距逐渐缩小，其目标函数设置为[12]

(12)

按梯度下降法调节神经网络的权值，反向修正各权值的大小，首先须要计算隐含层至输出层的权值，其逐步迭代更新的公式为

(13)

式中：η表示学习速率。

然后计算输入层至隐含层的权值，其逐步迭代更新的公式为

(14)

1.4 温室系统模型的建立

在温室系统中，与温度、湿度相关的控制量有很多，影响两者的主要因素是加热、加湿和通风，针对北方的日光温室，主要考虑冬季环境，温室温度的增加主要依靠加热系统，降温可以通过通风形成空气对流和水分蒸发来实现；湿度对温室中作物的生长也很重要，可以通过加湿器或湿帘水分蒸发增加湿度，温度升高也会使水分蒸发加剧，由于温室外湿度一般低于室内，因此降湿也可以通过通风实现。

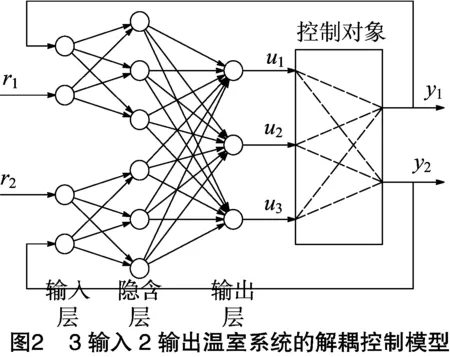
综上可知，控制对象是一个3输入2输出的形式，控制输入包括加温、加湿和通风，控制输出包括温度和湿度，输入和输出之间形成相互耦合的关系。将MPIDNN控制器和控制对象结合，形成一个闭环控制系统(图2)。

由图2可知，MPIDNN控制器是一个4输入3输出的神经网络，其输入端r1、y1表示温度的目标值和实际值，r2、y2表示湿度的目标值和实际值，神经网络的输出值u1、u2、u3是控制对象的控制量，分别表示加温、加湿、通风。目前针对温室系统的模型研究，应用较广泛的是Albright提出的模型[13-14]：

(15)

式中：Tin、Tout分别表示室内外温度，℃；Hin、Hout分别表示室内外湿度，kg/m3；ρ表示正常环境下温室系统内的空气密度，kg/m3，通常取值为1.2 kg/m3；Cp表示温室内空气比热容，kJ/(kg·℃)，通常取值为1.03 kJ/(kg·℃)；V表示温室单位面积上的等效体积，单位为m3/m2；Qheater表示加热速率，J/(m2·s)；Qfog表示喷雾速率，kg/(m2·s)；Iin表示温室内吸收的太阳辐射，W/m2；φvent表示通风速率，m3/(m2·s)；Ke表示室内外空气传递系数，W/(m2·K)；E表示蒸发蒸腾速率，kg/(m2·s)；λ表示水蒸发系数；α、βT分别表示比例系数。

该模型考虑到温室系统中加热、喷雾、通风对系统温湿度的影响，还包括光照等因素的影响，为了便于研究，对模型的等式方程(15)进行分析归纳，可以得出3输入2输出温室系统的简化模型，其形式为

(16)

2 基于PSO算法优化PIDNN实现过程

2.1 PSO简介

粒子群优化算法是一种新的进化算法(EA)，具有参数少、易理解、易实现的优点，且有较强的全局搜索能力，是一种很好的优化工具[15]。

粒子群优化算法运算，首先要对选定的自变量进行初始化，即选定一群随机解，然后通过多次迭代找到目标的最优解。在算法的迭代优化运算中，须要通过一定的方式来进行自我更新，这涉及到2个极值，分别是个体极值和全局极值，个体极值就是在粒子搜寻最优解过程中自我记忆和当前速度对粒子的影响，通过自身找到的最优解；全局极值是粒子受到整个群体的影响，整个粒子群在整个群体中找到的最优解。

在运用粒子群算法优化时，通过找到2个最优位置，即个体极值和全局极值，迭代更新粒子速度和位置，迭代规律根据公式(17)进行。

(17)

式中：vid表示粒子的速度；xid表示粒子的位置；pid表示粒子的个体极值；pgd表示粒子的全局极值；w表示惯性权重；r1、r2表示加速度权重系数；c1、c2表示学习因子。

2.2 基于PSO算法优化PIDNN实现过程

PIDNN是神经网络的一种进化形式，具有常规PID和神经网络两者的优点，同时也是有神经网络学习速率低、收敛速度慢的缺点，为了满足更高的控制要求，须要提前将神经网络的各项权值进行优化。本研究提出的MPIDNN控制器是一个4输入3输出的神经元网络，网络中包括从输入层到隐含层的12个权值以及从隐含层到输出层的18个权值，共须优化的权值为30个，因此首先须要PSO算法优化的是一个30维函数。

通过PSO算法将PIDNN的30个权值进行优化，运算出合适的权值作为MPIDNN控制器的初始值，通过给定控制器输入值，将输出的输出值作为控制对象的输入值，对温室系统模型进行调节，使系统的温湿度状态维持在理想的范围内。

3 温室系统的仿真研究

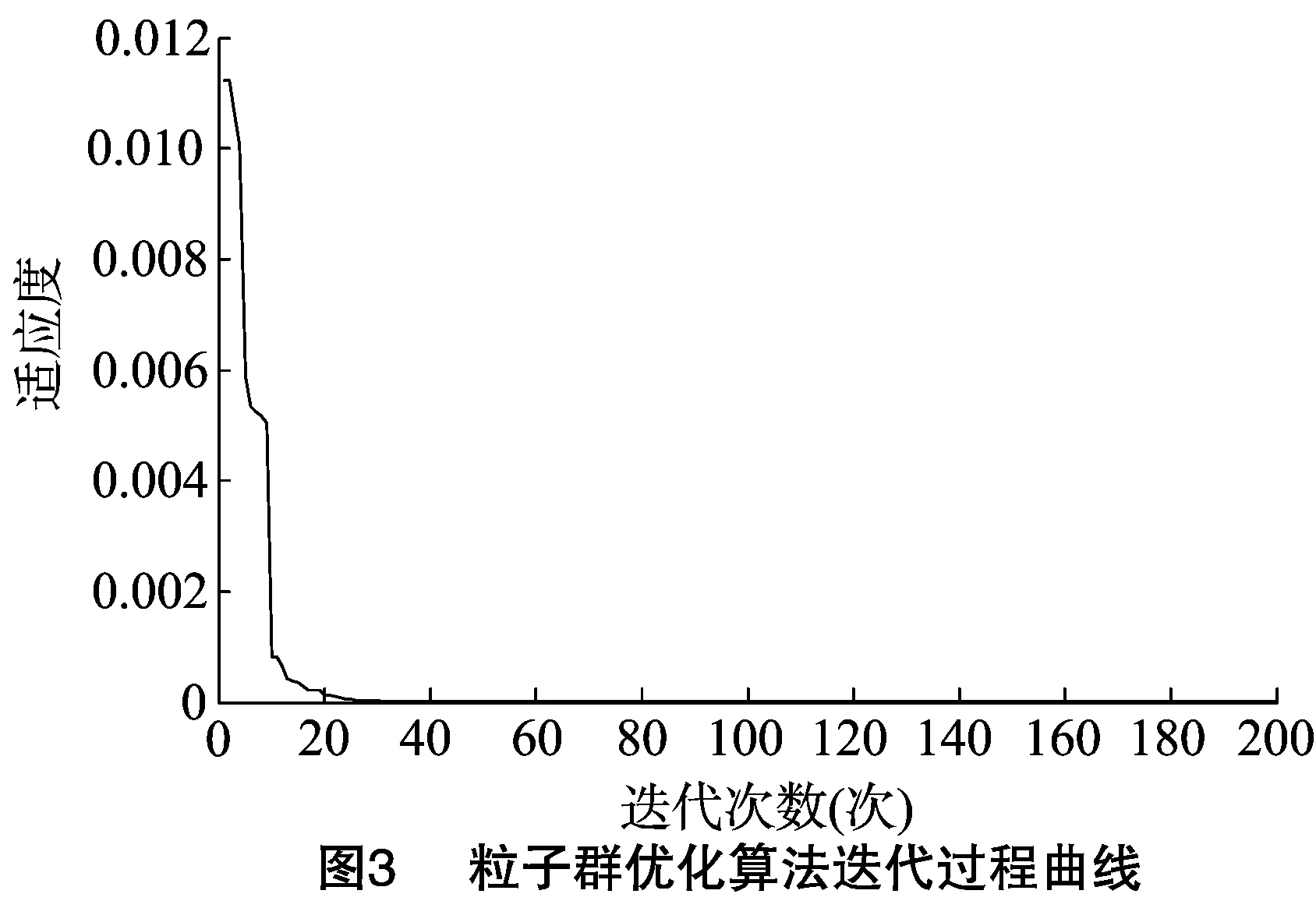
对基于PSO的PIDNN进行仿真试验，将粒子群种群数设置为100个，迭代次数设置为200次，自变量个体数设置为30个，粒子群的学习因子设置为c1=c2=1.494 45。MPIDNN控制器的输入设置为r1(k)=0.5，r2(k)=0.7。应用公式(14)的简化模型方程可得仿真结果。

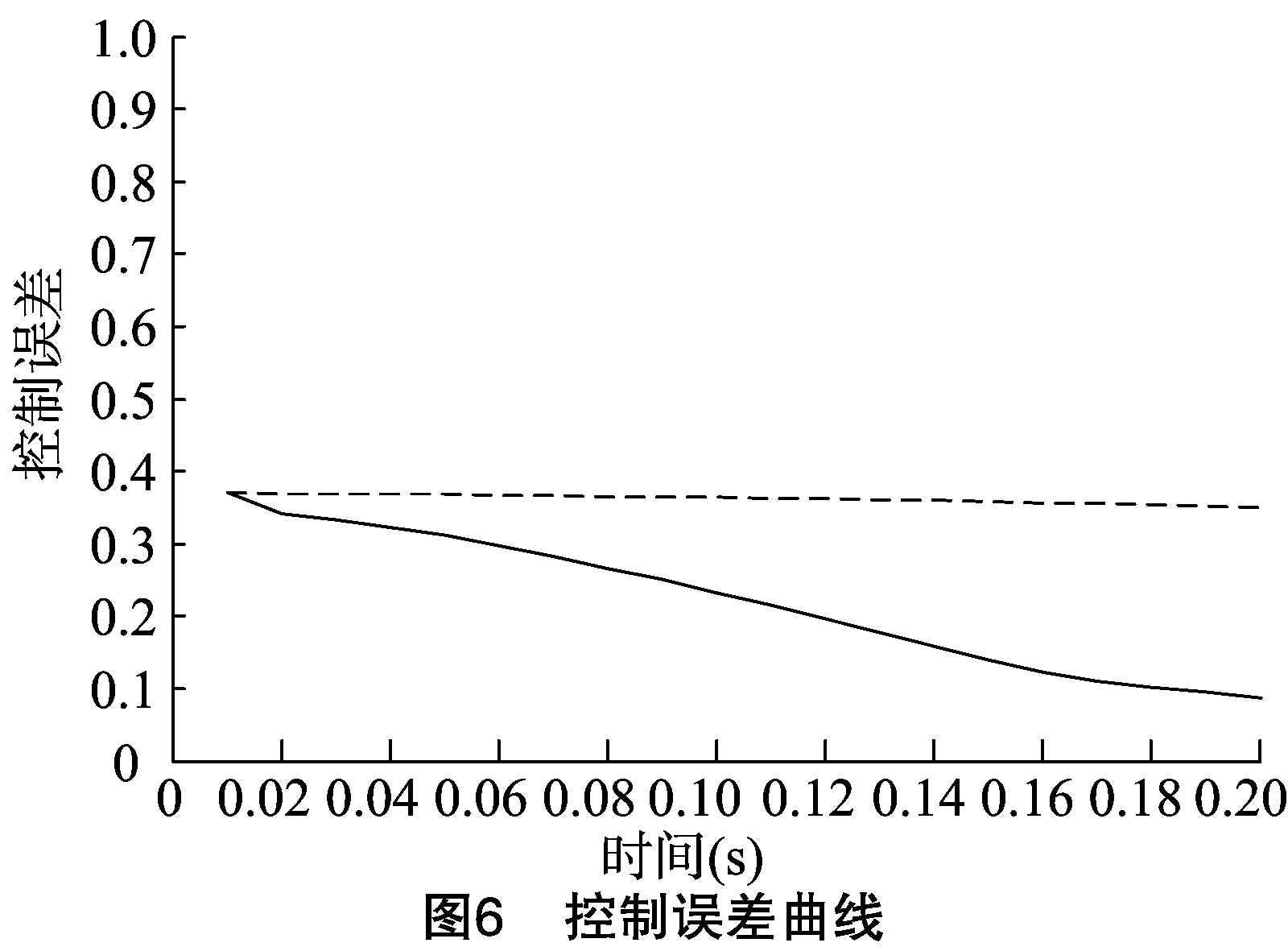
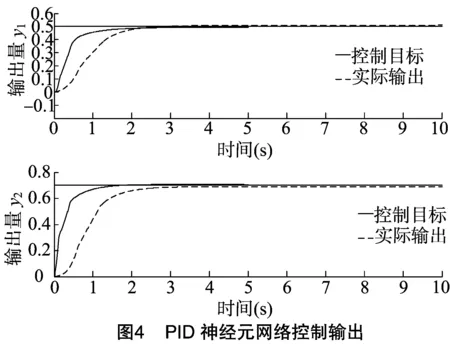
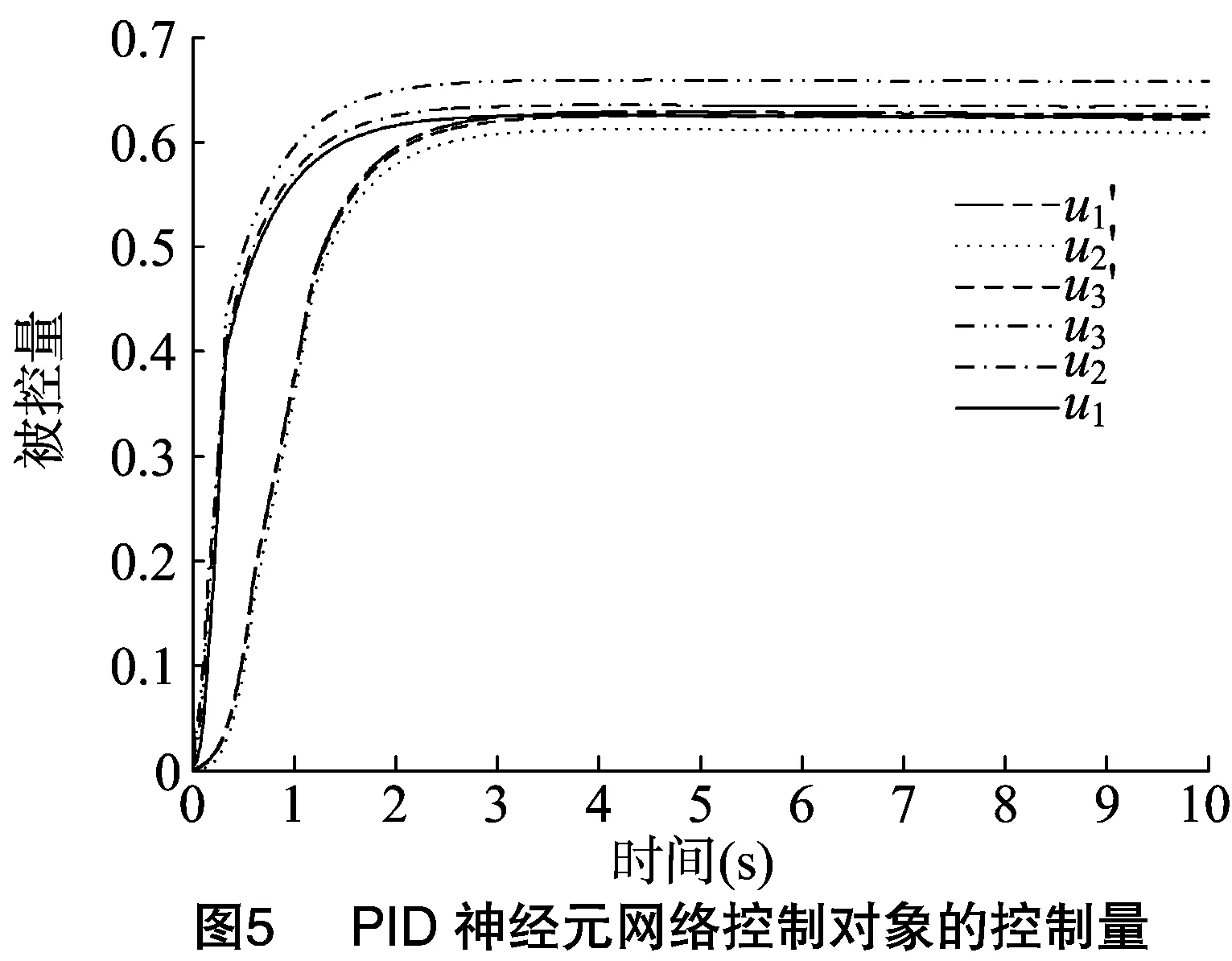
由图3可知，迭代到第36次时，找到最优值。图4、图5分别表示控制系统的2个输出值和控制器的3个输出值，亦是温室系统的状态值和控制对象的输入值，虚线表示PIDNN为控制器时的系统状态，实线代表PSO-PIDNN为控制器时的系统状态，2种控制器相比，经过PSO优化的控制器快速响应性好和稳定性高，解耦效果较突出。图6是控制系统的控制误差曲线，表示控制系统输出量和输入量之间关系，通过曲线可以看出，经过PSO优化的PID神经元网络控制器对于系统的优化，具有更好的控制作用，控制性能更加良好。

4 结论

本研究通过探讨温室系统控制对象中的温湿度耦合状态，并分析控制输入和控制输出之间相互耦合，提出基于PSO算法的PID神经元网络控制模型，通过PID神经元网络控制器可以解决常规PID无法解决的耦合问题，且运用神经网络的自适应性能够动态修正网络权值，考虑到PID神经元网络初始权值的随机性，首先通过PSO算法对PID神经元网络权值进行优化，仿真结果表明，本研究提出的方法使温室系统温湿度解耦效果明显，且系统稳定性、快速性都有明显提高，控制系统的鲁棒性增加，该方法对于温室系统的多输入多输出模型有很好的解耦能力，是一种有效的策略。