蠕虫状链模型的均方末端距修正

刘引烽,周 洁

(上海大学材料科学与工程学院,上海200444)

高分子链在空间的形貌是高分子柔性的一种表现形式,也是高分子链的基本特征之一.如何运用数学模型来了解高分子链在空间的形貌和基本尺寸,是高分子物理学的基本内容.

蠕虫状链一直是分析DNA等生物大分子常用的模型,也是半刚性和刚性链高分子较为通用的模型.本工作对蠕虫状链模型作一介绍,并对均方末端距推导过程中存在的问题加以分析,最后提出解决方法.

首先简要回顾一下几种理想链模型.在高分子链的各种模型[1]中,最简单的理想模型就是自由结合链.所谓自由结合链,就是把链中最基本的结合单元化学键看成是相互自由连接的.这些键在相互连接时,没有键角限制、化学键没有体积,键在空间的取向完全自由、没有位垒及其他任何阻碍其链接的额外限制.每个键在与前一个键连接时,在空间的取向完全是随机的.这样,由n个键长为l的键所组成的链就是自由结合链,其均方末端距很容易用矢量和的平方平均或用无规飞行的统计分布函数进行平均而得到:

当引入键角限制而其他条件不变时,自由结合链就转变为自由旋转链.这种模型链在统计处理时所遇到的难题,是非直接相连的两个键矢量之间(j＞i)点积的计算问题.将键矢量反复向前一个键矢量方向进行投影,直至抵达需要相乘的键矢量就可以方便地解决这一难题,所得自由旋转链的均方末端距为

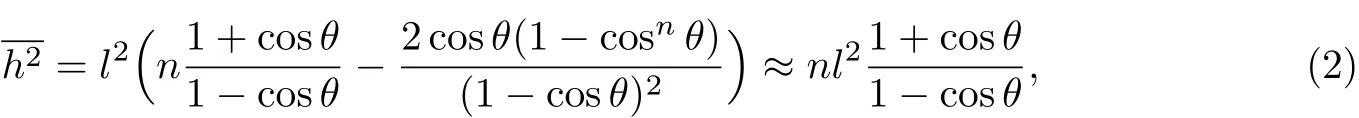
式中,θ是键角α的补角,即θ=π-α.

在实际高分子链中,化学键的旋转除了键角限制外,相邻基团对其旋转也会产生很大的影响,因所处位置不同而具有不同的旋转位垒,同时化学键、原子和原子团都是有体积的,一旦占据了某个空间就不再允许其他键或原子(团)进入,存在体积排斥效应等,因此实际高分子链的均方末端距要比自由旋转链大得多.由于实际高分子是受阻旋转链,其均方末端距的计算就需要引入一个刚性因子,在理想的自由旋转链模型与实际链之间搭建关系桥梁:

式中,σ为实际链的刚性因子.

在处理实际链时,若其基本连接单元不用键来表示,而是放大到能够自由连接的“链段”,那么连接单元长度就成为le,而连接单元的数目就会随之减少为ne,即链段的长度为le,链段的数目为ne.倘若ne仍然是一个庞大的数字,可以满足统计法则,那么这种链仍然可以运用自由结合链的模型来处理,称为等效自由结合链.由于这种链的末端距在空间的分布符合高斯分布,因此又被称为高斯链,其均方末端距为

由上述方程容易看出,无论哪种模型得到的均方末端距都与统计单元数目的一次方成正比,而单元数目恰恰与分子量是线性相关的,因此均方末端距与分子量呈线性正比关系.用均方末端距除以链的分子量就可以得到一个能表征分子链刚柔性的特征参数——分子无扰尺寸:

但是,实际链并不总是那么理想.如果链刚性较强,使得用于统计的连接单元的长度过长,或者尽管高分子链本质是柔性的,但其分子量过低等,在这些情况下,分子链的统计单元数不能达到满足统计意义的数值,上述模型就无法施展其功用,此时就要借助另一种模型——蠕虫状链(worm-like chain,WLC)来了解分子链的空间尺寸.

1 蠕虫状链的基本处理方法

蠕虫状链是Porod和Kratky在1949年提出的概念[2],因此蠕虫状链又称Porod-Kratky链.无论统计单元数是多少都可以用这种链模型进行处理,因此蠕虫状链既可以描述柔性链,也可以描述刚性或半刚性高分子链,还可以描述分子量较低时的齐聚物柔性链.

下面介绍一个持续长度的概念,它是蠕虫状链模型中的重要参数.对于一条由键长为l、键角为α的n个键所组成的大分子链,将第一个键的方向看成z轴(见图1),那么第二个键以α角与之相连,键矢量间的夹角为θ,第三个键又以α角与第二个键相连,其键矢量间的夹角亦为θ,依次类推,这条链的末端距在z轴上投影的平均长度即为n个键矢量在z轴投影长度的加和:

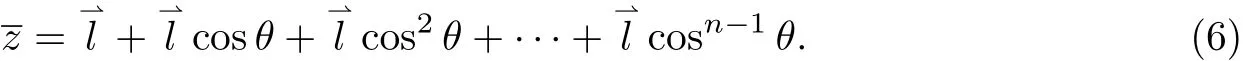
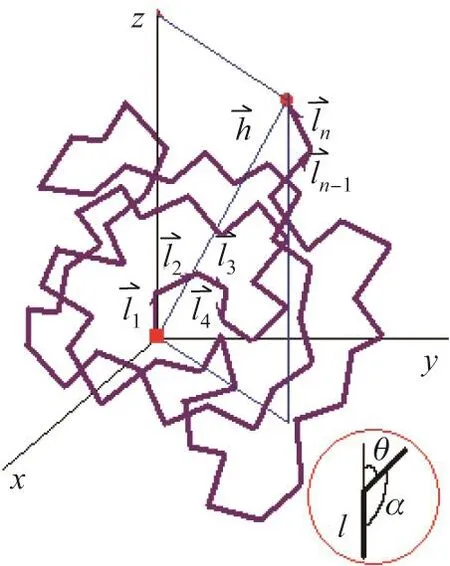
图1 大分子链在第一个键的方向上投影示意图Fig.1 A polymer chain and its projection in the direction of the first bond

由于cos θ＜1,因此有

当n→∞时,cosnθ→0,则的极限值为

该极限值仅与键长和键角有关,与分子量无关,定义为持续长度,用a来表示,即

因为a与分子量无关,也可看成是链本质的特征参数,表示一条链保持某个特定方向的倾向,也反映了高分子链的刚性尺度.对于有限长度的分子链而言,持续长度不能反映其真实的链尺寸,此时就需要利用蠕虫状链模型,采用平均投影长度进行处理.

对于一条由n个键长为l、键角为α的键所组成的分子链而言,蠕虫状链模型把键长无限分割,这样键角逐渐趋于180°,θ角无限缩小并趋于0°,而键长l也逐渐减小,n值则逐渐增大,且保持轮廓线长度L=nl不变.这就是蠕虫状链模型,它是假想的线性链,是含有无穷细的连续曲率的链,任一点曲率方向都是无规的,是一种适用于研究半刚性分子链,尤其是齐聚物链和刚性分子链构象的简化模型链.

利用如下级数关系:

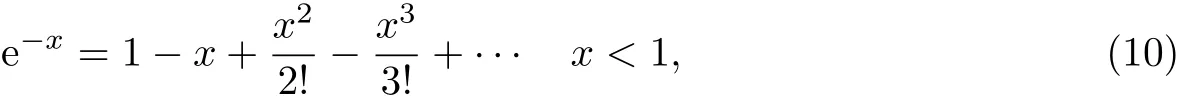
将x替换成1-cos θ,则e-(1-cosθ)≈ cosθ((1-cosθ)＜ 1),所以

于是,链在第一个键方向上的投影长度z可表示为

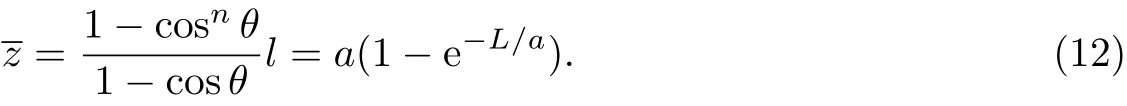
2 蠕虫状链的均方末端距

采用蠕虫状链模型处理分子链时,主要用投影长度来表示分子链尺寸,那么其均方末端距与投影长度、持续长度及总长有何关系呢？目前通用的方法是经典的Porod和Kratky(P-K)方法,借用何曼君等编著的《高分子物理》[1]介绍P-K方法如下.

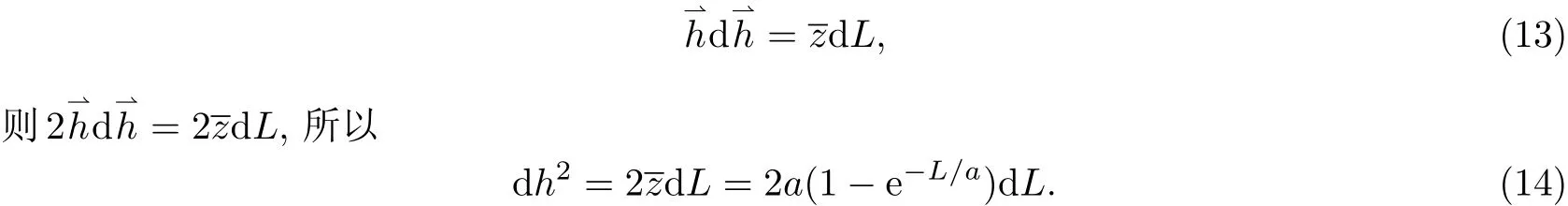
积分可得:

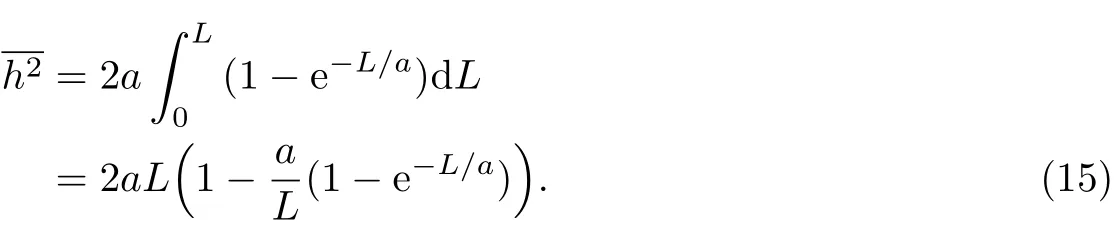
根据自由旋转链的均方末端距公式(2),代入基本变量关系L=nl及式(9)和(11),当cos θ趋近于1时,可得

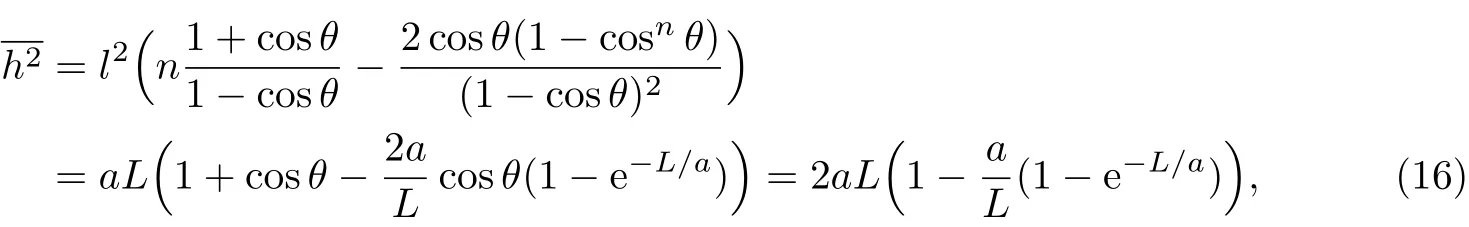
可见与蠕虫状链的表达式一致.

3 蠕虫状链均方末端距处理方法质疑

蠕虫状链中的连接单元是假想的自由旋转链,P-K方法所得均方末端距表达式如式(15)所示.仔细分析这种蠕虫状链均方末端距的处理过程不难发现其中所存在的问题.

式(13)右边是标量乘积,左边则是矢量点乘,其中一个是末端距矢量,另一个是在z轴上链延伸的极小量,其点积可以看成是矢量在方向上的投影与的乘积,而在方向即z轴上的投影正好是投影长度的模为dL,因此该式成立.

那么为什么在cos θ趋近于1时,其计算结果又与自由旋转链一致呢？这是因为P-K方法增设了一个前提条件,即cos θ趋近于1,此时键角趋于π,链的方向趋近于z轴,因此能近乎满足第一个键在z轴,而末端距也几乎落在z轴方向,即满足了末端距h与dh是同一个方向的条件.矢量同向条件满足,从而由式(13)到(14)便顺理成章,导致此时蠕虫状链末端距与自由旋转链结果一致.这就是为什么对刚性链,蠕虫状链与自由旋转链结果可以一致的原因.不难进一步导出此时链的均方末端距为

即均方末端距约为伸直链长度的平方.显然,这是典型的刚性链.

我们也可以看一下蠕虫状链对于柔性链的模拟,以便与自由旋转链相比较,来了解其不一致之处.在存在键角的情况下,?最为柔性的?模型链就是自由旋转链了.对于这种柔性链,因为L≫a,因此≪1,蠕虫状链均方末端距表达式(15)中的后一项可忽略,则其均方末端距为

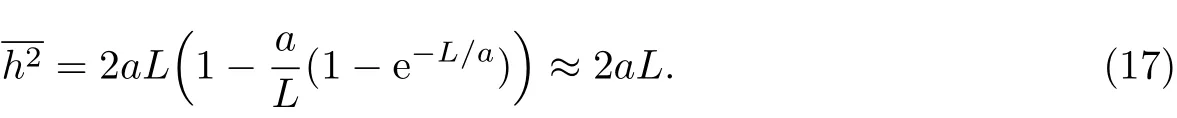
对于C-C键,其键角的补角约为70.5°,此时自由旋转链的持续长度可以通过式(9)计算得到:

故对于C-C链形成的自由旋转链,以蠕虫状链计算所得均方末端距为3nl2.再根据L=nele,而h2=nel2e,由方程式(17)可算得a相当于链段长度le的一半.而以方程式(2)计算的均方末端距结果为2nl2,与蠕虫状链结果相差1.5倍,这就说明蠕虫状链在模拟柔性链时与自由旋转链是不一致的.尽管差别不是很大,但是数学上的不严密是蠕虫状链模型在推导均方末端距时的一处“硬伤”.

4 解决方法

事实上,在求解蠕虫状链均方末端距时,我们认为完全可以不用通过积分方式来求取,而仍采用自由旋转链求解均方末端距的方法.由于末端距矢量由键矢量加和而得:

这样就可以得到键角为α、补角为θ的自由旋转链均方末端距求解公式,即式(2):

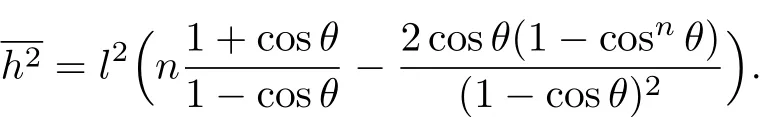
将式(9)和(11)及L=nl代入式(2)中,得到:

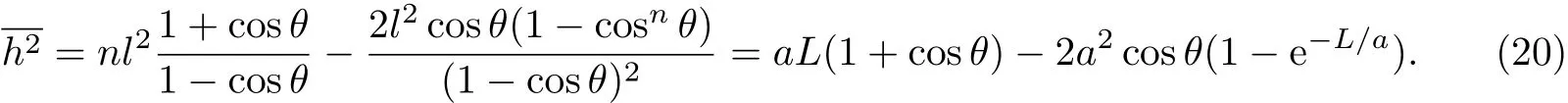
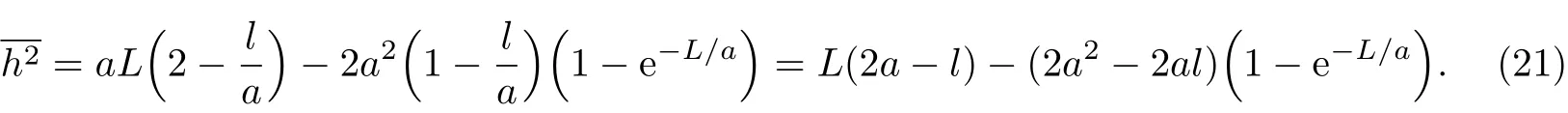
对于n很大的柔性链,因为L≫a,因此e-L/a→0,则均方末端距关系式(21)可简化为

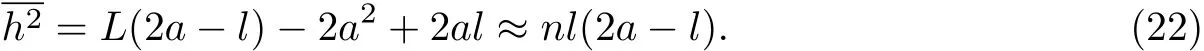
对于C-C键形成的自由旋转链,a≈1.5l,所以其均方末端距为h2≈2nl2,与自由旋转链结果一致,此时le=2a-l≈2l.

对于刚性高分子链,因为a值很大,从理论上讲,刚性链的a可以趋于无穷大,例如全反式聚乙炔链的a即为无穷大,此时L≪a,e-L/a可以用级数展开,则式(21)可化为

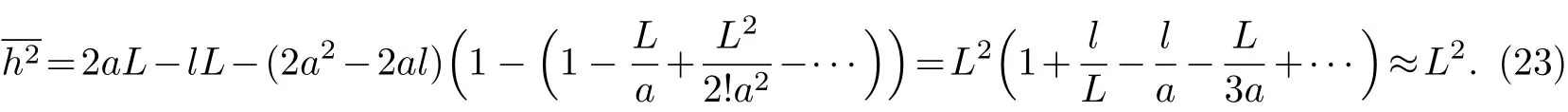
对于半刚性链,若其极限投影长度等于伸直链长,即a=L,则

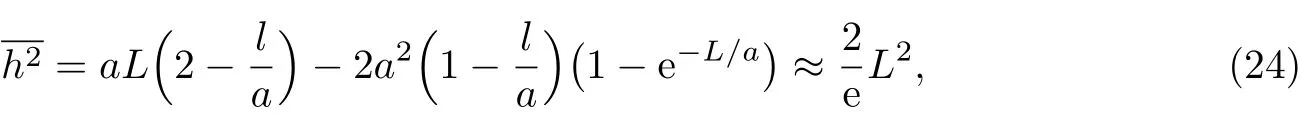
可见其均方末端距比完全刚性蠕虫状链的均方末端距略低,也具有刚性链的特征.

显然,通过上述处理,蠕虫状链与自由旋转链对于柔性链的描述就一致了,并且可以运用于刚性链体系.

5 持续长度的讨论

蠕虫状链的处理方法非常巧妙,它化解了统计单元数必须很大的难题.因此,一般认为这一模型的适用面更广.

自Porod和Kratky提出蠕虫状链模型以来,运用此模型处理诸如DNA等较为刚性长链的研究逐年增多.近年来,随着DNA研究的迅猛发展,蠕虫状链模型也重新被广泛应用.例如,有关蠕虫状链模型应用的文献自2006—2016年的十年间累计达1 552篇(数据来自SciFinder数据库).因此,厘清一些基本概念就显得非常重要.

持续长度是该模型的一个基本参数.持续长度与自由旋转链的处理方法有异曲同工之妙,因为二者都采用了后键依次在前一键上投影并依此前推至所需键的计算方法.自由旋转链因为需要所有键之间进行两两点乘,因此其平均范围广,需要大量样本的统计平均方可采用投影法进行平均处理.持续长度涉及的是各个键在第一个键方向上投影,一旦键的方向与第一个键相反,它在z轴方向的投影就是负值.经平均处理后,负值就不再出现,代之以收敛于0的投影值.因此,持续长度的计算同样应该是大量连接单元的统计平均值.

持续长度a反映了链本身的刚柔性,a值越大,表明链的刚性越强.根据式(9),对于自由结合链,θ是0°～180°间的任意值,因此其平均值趋于90°,连接单元长度为键长l,此时a值达到最小值l;而对于自由旋转链,仅存在键角限制.如聚乙烯类碳链高分子,其C-C键的键角α为109.5°,其a值约为1.5l,略高于自由结合链;对于键角为120°的高分子,其a值理论上约为2l.对于全反式聚乙炔等刚性高分子而言,由于共轭双键不能内旋转,因此需要将两个键作为一个整体单元来看待,单元长度是键长的2倍,单元数则是键数的1/2.这样这些单元间的连接成为180°键角的连接,a值将趋于无穷大.对于蠕虫状链模型研究较多的DNA,当链段数趋于无穷大时,其持续长度a可能为35～50 nm[3-4].假定这种DNA中核糖或脱氧核糖五元环的尺寸l约为0.3 nm,则可反推出其键角补角θ约为6.3°,因此键角约为173.7°,非常接近于刚性直线连接.当然这种键角是不存在的,采用蠕虫状链模型时,连接单元不一定是真实键,而是假想键,这种假想键是自由旋转的,其“键数”、“键长”和“键角”与真实分子链的实际参数相关.

6 投影长度的讨论

从式(12)可见,高分子链在第一个键方向上的投影长度z仅是a和L的函数,其中a是常数,是链长趋于无穷大时的极限投影长度,它反映了大分子链的本质,组成链的键长l越大、键角α越大或者说其补角θ越小的大分子链,刚性越大,a值越大.投影长度z与链的总长L的关系如图2所示.由于链长L与分子量M是一次方的正比关系,因此高分子链在第一个键方向上的投影长度和分子量间的关系与之类似,也可以用图2的曲线形式来表示.在自由旋转链模型中,均方末端距与分子量是线性关系,而蠕虫状链的投影长度与链长或分子量间的关系则呈指数趋近关系,随着链长或分子量的增加,投影长度逐渐增大,链长趋于无穷大时,投影长度趋近于a值.

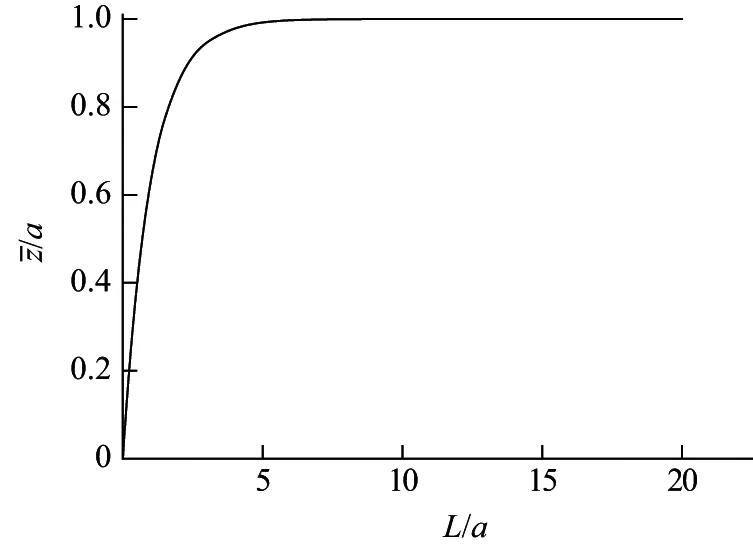
图2 投影长度与链长的关系Fig.2 Persistence length vs.chain length

7 存在的问题与展望

通过自由旋转链模型对蠕虫状链的均方末端距进行统计,可以纠正原有模型在推导过程中的错误,所得结果既可以用于模拟刚性链,也可以用于模拟柔性链,因此有助于蠕虫状链模型得到正确而广泛的应用.

然而,蠕虫状链模型也存在一些不足.由于蠕虫状链用投影长度来表示分子链尺寸,看上去没有用到统计单元数的统计关系,统计单元的多寡仅影响其投影的长度,不影响计算结果,因此可用于描述那些因统计单元数不足而无法用等效自由结合链来处理的分子链.但实际上,不断投影取最后的投影长度的方法也是统计的结果.这种暗含式的统计处理方法很隐蔽,使人们在将其运用到刚性链时没有觉得有什么不妥.

对于柔性链而言,a值是链长趋于无穷大时投影长度的极限,因此是链投影长度的最大值.链段的数目越少,投影长度也越小.但刚性链不同,因为链是刚性的,链的投影长度用cos θ依次向前一键进行投影的方式就不合理.能够作投影处理的前提条件是键可以在锥形面上取得任意位置,并可以进行统计平均(见图3).把刚性链中的键无限分割,虽然已经把柔性链“揉”到一个键中了,但并未影响链的整体属性.因此,对于刚性链,由于分子链伸展的可能性较大而蜷曲的可能性较小,即受到内旋转位垒的限制,高分子链的“回头率”是很低的.随着总长的增加,分子链的投影长度是持续增大的,导致a值有可能并不收敛于某一定值,即不再满足式(9),而是会趋于无穷大.但就在这些持续长度趋于无穷大的链中,其刚性也会有所不同,如何加以区别？如何模拟具有不同刚性的刚性链？这还需要今后深入研究加以解决.

图3 单键内旋转示意图Fig.3 Inner rotation of a bond within a polymer chain

运用经典的蠕虫状链模型来描述DNA等刚性分子已很普遍[5-8],持续长度也可以用计算机进行模拟[9-10],投影长度对分子链形态的描述也有其独到之处[11-12].随着高分子科学向生命物质的不断渗透,采用蠕虫状链模型来处理分子链形态与构象关系将越来越多[13-15].为此,更正一些不当的处理过程,发展计算机模拟方法,将使蠕虫状链模型得到进一步的发展和补充.