模块化可展开抛物柱面天线展开机构设计与仿真

董自瑞

(南京航空航天大学 航天学院，江苏 南京 210016)

0 引言

星载天线展开机构属于空间三维展开机构，是空间可展开机构中结构最复杂、功能最重要的部分，其发射时折叠为一个可以接受尺寸的系统(收拢状态)，而在达到预定轨道后通过展开机构按设计的方式解锁、展开、锁定，展开成为天线(展开状态)。可展开机构有效口径和形成的型面精度决定了卫星通信的频率波段和质量。随着航天技术的发展，星载天线形成了大口径、高精度、轻量化的发展趋势。但是考虑火箭搭载能力有限以及搭载发射的成本，对大型可展开天线提出了较高要求的收纳比。

目前很多国家对星载可展开天线机构进行了研究。其中，ETS-VIII卫星天线[1-2]是日本航空设计的两个平面桁架系可展开机构，于2006年12月26日发射成功。如图1所示，天线由14个直径4.8m模块组成，展开口径为19.2m×16.7m，收拢高度和直径为4m×1m，每个模块由6个完全相同的肋组成。

图1 ETS-VIII卫星天线展开、收拢图

SMAP卫星[3]是NASA于2015年1月31日成功发射人类首颗用于“土壤水分主被动观察卫星”。SMAP卫星天线采用周边桁架式可展开机构，外圈是通过平行四边单元组成，通过改变对角线长度来实现机构的整个天线收拢展开，展开口径达6m(图2)。

图2 SMAP卫星天线地面展开图

国内主要以浙江大学空间结构研究中心设计的环形桁架式、四面体式和正六棱柱式天线支撑机构，建立了可展开机构过程分析理论，应用广义逆理论对结构稳定性转化问题进行了分析，提出了具有位移约束的空间结构的分析方法[4]。

中国空间技术研究院西安分院研制出空间四面体式和径向可展开肋天线机构原理样机(图3)。四面体天线支撑机构展开口径 6m×2.8m。

图3 空间四面体天线支撑机构图

1 模块化单元几何建模

抛物柱面可展开支撑机构主要由沿着柱面母线方向的纵向肋单元和沿着抛物线方向的横向肋单元组成，横向肋和纵向肋结构相同，通过调整横向斜杆尺寸形成夹角，来拟合抛物线。横向、纵向肋单元组成一个十字模块单元，通过十字单元拓扑即可得到抛物柱面结构(图4)。

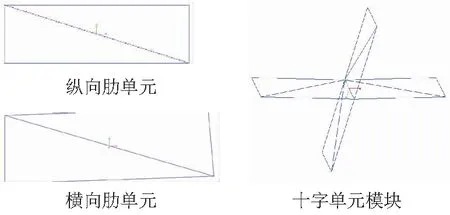
图4 模块单元几何图

十字单元模块拓扑即可得到所需的抛物柱面天线口径，但总体机构四周并无实际意义，如图5(a)所示，需要进行机构优化，去除冗余部分。抛物柱面支撑机构的刚度决定了拉网所形成天线型面的精度，需要对模块单元进行加强，提高刚度从而达到增强型面精度的目的[5-6]。

在十字单元连接处增加纵向辅助肋和横向辅助支撑杆，如图5(b)所示，提取优化后田字单元模块(图6)。单元模块具有对称性，本文主要模块单元进行设计分析与仿真。

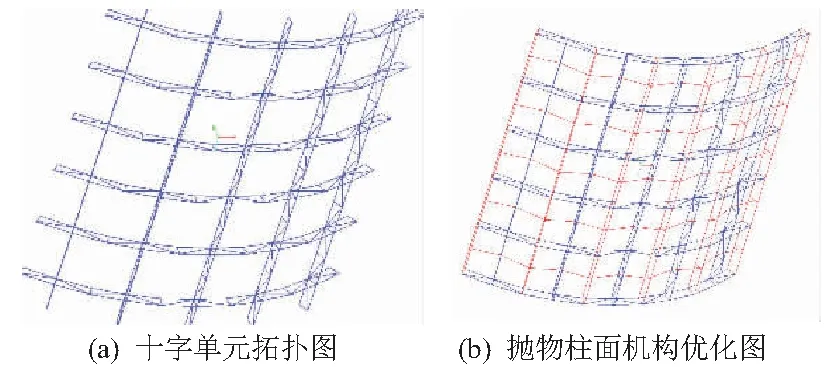
图5 抛物柱面天线机构组成图

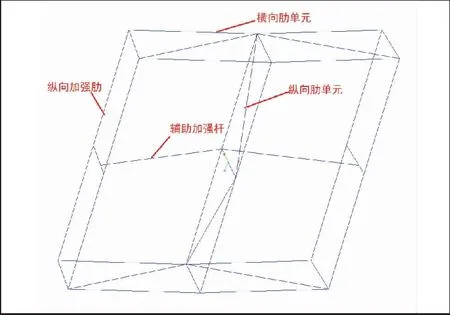
图6 田字单元模块几何图

2 单元模块展开机构设计

肋机构设计借鉴了台湾学者颜鸿森提出的颜氏创造性设计法，提取EST-VIII构架式展开天线基本单元运动原理(图7)，在抛物线方向通过展开机构与拉索作用在金属网面形成抛物线，在柱面方向通过矩形肋拓展即可得到柱面[7-8]。

图7 卫星天线展开机构横向肋工作原理图

图8为横向、纵向肋单元机构采用相同的驱动方式，弹簧驱动滑动副使得机构展开；通过调整部分杆件的长度使得纵向肋单元模块展开后为矩形、纵向肋单元模块展开后上杆与水平方向存在预定夹角。图9为1/4模块收拢展开图。

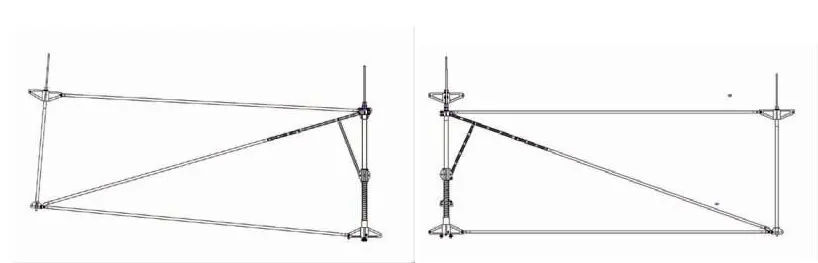
图8 横向、纵向肋单元设计图

图9 单元基本模块展开收拢图

在抛物线方向和柱面方向增加基本单元数量即可得到所需要的口径的抛物柱面天线；由于空间展开机构多为杆件，切口径大，型面精度高等特点，展开后静稳定性要求高，需要对机构布局相应的钢丝绳来增加稳定性和提高刚度。图10为整体展开收拢状态。

图10 展开机构整体展开收拢图

3 单元肋运动学分析

采用复数矢量法对单元肋进行运动分析，通过设定驱动滑块位移、速度来求得各个关节角位移、角速度。进行肋单元机构运动学分析时，首先按照矢量封闭多边形列出复数矢量方程，再将肋单元分成3个回路进行分析，按照矢量封闭多边形列出矢量方程。

3.1 回路1运动分析

1) 位移分析

图11为回路1机构简化图，式(1)为复数矢量方程：

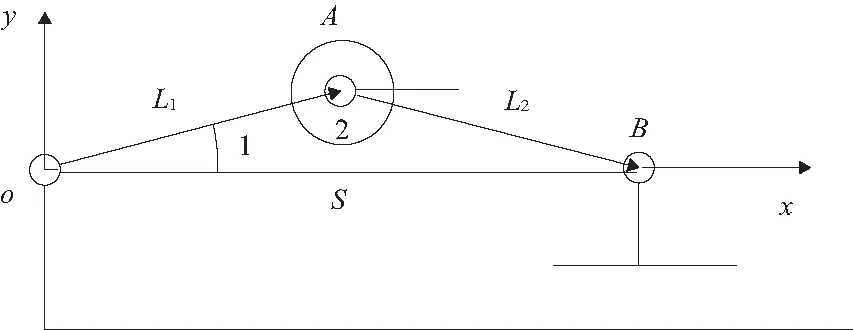
图11 单元肋回路1机构原理图

(1)

分别取实部虚部得：

S=L1cosθ1+L2cosθ2

(2)

L1sinθ1+L2sinθ2=0

(3)

2) 速度分析

将式(1)对时间求导，得：

(4)

由此解得：

(5)

(6)

3) 加速度分析

将式(4)对时间求导：

(7)

得：

(8)

(9)

3.2 回路2运动分析

1) 位移分析

图12为回路2机构原理图，式(10)为五边形矢量方程：

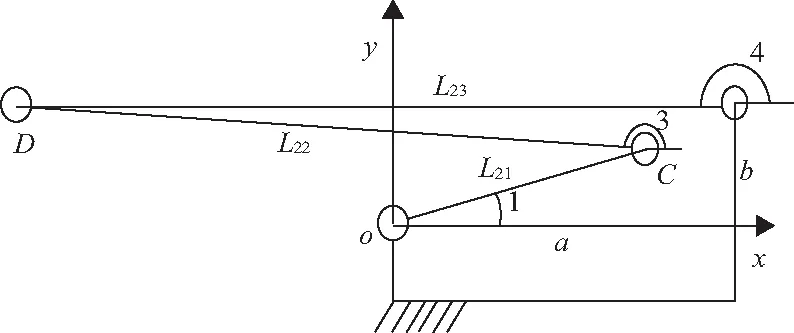
图12 单元肋回路2机构原理图

(10)

在两轴分解：

L21cosθ1+L22cosθ3=a+L23cosθ4

(11)

L21sinθ1+L22sinθ3=b+L23sinθ4

(12)

依据式(11)、式(12)可解出θ3、θ4。

3.3 回路3运动分析

1) 位移分析

图13为回路3机构原理图，式(13)为五边形矢量方程：

图13 单元肋回路3机构原理图

(13)

在两轴分解：

L31cosθ6+L32cosθ5=a+L33cosθ4

(14)

L31sinθ6+L32sinθ5=b+L33sinθ4

(15)

依据回路2的θ4求出，可解出θ5,θ6。其中θ6为天线支撑机构展开过程直接输出参数，可作为天线展开状态的描述依据。

3.4 模块化抛物柱面天线支撑机构运动学分析

对于支撑机构展开运动学仿真，可以验证机构展开的可靠性。模块化可展开抛物柱面天线支撑机构多采用重复单元模块，且基本单元模块的肋单元机构相同，关键部件杆长不同。通过对基本单元模块的仿真，可以得到肋单元滑块位移角度变化关系参数曲线。在进行整机运动学仿真的时候，可以去除部分辅助加强机构，在不影响整机展开可靠性的情况下，可以得到主要形成天线型面支撑点的运动轨迹，为地面试验提供参数设计依据[9-10]。

1) 展开角度运动学仿真

将装配体模型在Pro/E与ADAMS接口、MechPro接口添加运动副，在Adams中给主驱动添加1mm/s驱动速度，滑块S位移100mm。如图14所示，在ADAMS软件仿真得到单元模块收拢展开图，验证样机单元模块可否展开，同时得到角位移随着滑块位移变化曲线，如图15、图16所示。

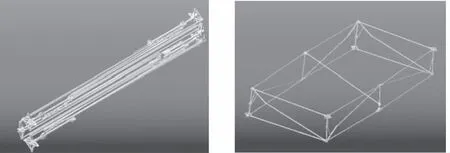
图14 两个单元模块收拢展图

图15 纵向肋关节展开角度与滑块位移关系变化图

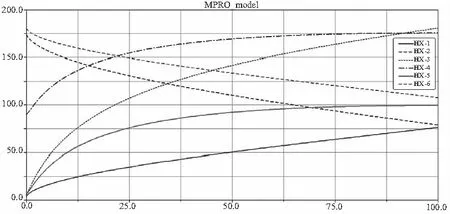
图16 橫向肋关节展开角度与滑块位移关系变化图

运动分析：θ6的角位移变化直接描述了单元肋机构的展开程度，且横向、纵向变化趋势相同；在驱动滑块匀速运动时候，横向、纵向展开角位一直增大且趋于平缓，说明机构可以顺利展开且角运动速度越来越小。

2) 单元模块对角线相对运动分析

由于空间环境的复杂性，展开机构在展开后除了靠驱动压紧力来保证机构的刚性，一般都会通过拉钢丝绳来增强整体机构的稳定性。对于单元模块对角线杆件之间的位移变化关系可以对钢丝绳设计走线提供参照，图17为基本单元四边形机构分布图。

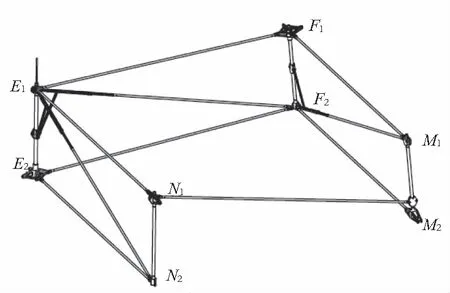
图17 基本单元四边形机构分布图

图18为四边形N1N2F2F1对角线及上下两边展开过程变化距离变化曲线。

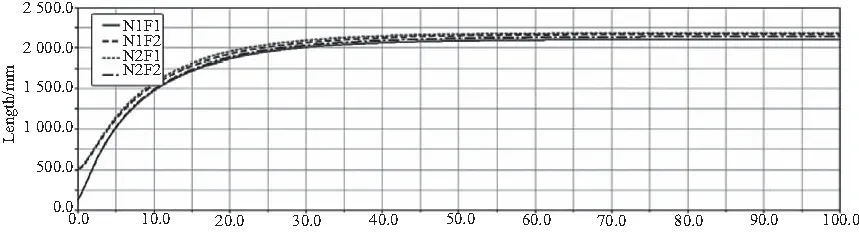
图18 基本单元对角线变化曲线1

图19为四边形M1M2E2E1对角线及上下两边展开过程变化距离变化曲线。

图19 基本单元对角线变化曲线2

图20为四边形M1M2N2N1对角线及上下两边展开过程变化距离变化曲线。

图20 基本单元辅助加强对角线变化曲线3

钢丝绳走线分析:基本单元四边形N1N2F2F1、M1M2E2E1两组角线变化基本相同，且单调递增，可以依据曲线变化设计钢丝绳走向。

3.5 多模块展开运动仿真

整体机构展开运动仿真对于地面验证十分有意义，考虑到机构是对称机构，简化模型的时候可以只针对一半模型进行仿真分析。图21为模块展开吊点轨迹图，得到构成曲面支撑点运动轨迹，为地面模拟吊挂实验设计提供参数依据。

图21 模块展开吊点轨迹图

将ADAMS跟踪得到的曲线在法相投影，并在MATLAB里汇总得到曲面支撑点运动曲线，如图22所示。

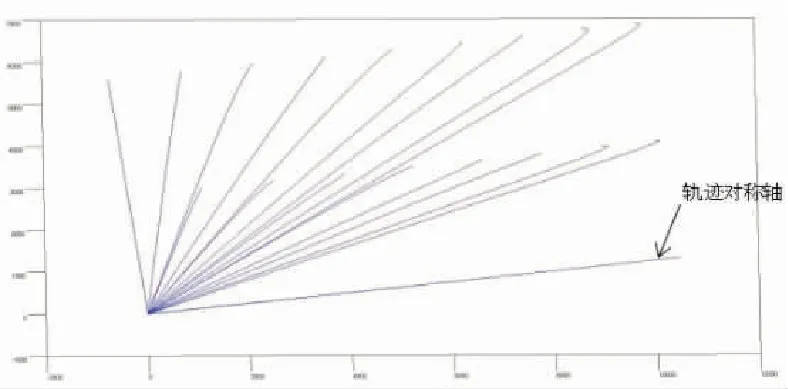
图22 整体模块展开吊点轨迹坐标图

4 结语

文章提出了一种利用十字单元肋来拓扑拟合抛物柱面机构支撑机构的方法，并对拓扑后的机构提出优化加强的思想；通过对单元肋设计完成基本单元的结构设计，并利用复数矢量法对单元肋进行了分析，得到滑块行程与机构各个展开角度之间关系；利用ADAMS软件仿真得到角位移与形成之间的参数曲线，分析机构对角线之间位移关系为增强刚度的钢丝绳提供设计依据；同时对1/2模型简化分析仿真，得到机构主要驱动点在展开过程的运动轨迹，为地面模拟实验提供设计依据。