轴瓦开槽的滑动轴承动压润滑数值分析
2019-01-08吴兆景徐岩李泷杲
吴兆景,徐岩,李泷杲
(南京航空航天大学 机电学院,江苏 南京 210016)
0 引言
滑动轴承是机械中常用的支承零件,其动压润滑性能对机械的稳定运行起着重要作用。常用的滑动轴承在轴瓦内壁上一般开有一个或多个半周或全周凹槽,主要为保证润滑油流通特性,但轴瓦凹槽结构对轴承特性有着重要影响[1],国内外学者对此进行过许多研究。文献[2]通过试验研究了两个轴向对称供油槽载荷方向的夹角对滑动轴承特性的影响,结果表明夹角在50°90°时润滑油冷却效果较好。文献[3]通过建模分析得出滑动轴承摩擦阻力系数随着矩形凹槽宽度的增加在不断增加。文献[4]通过对流体质点的流动轨迹的数值分析,得出螺旋槽在一定程度上导致滑动轴承油膜承载力降低。目前凹槽对滑动轴承的影响机理尚不清晰,尤其是凹槽延伸角度、宽度对滑动轴承润滑特性的影响规律尚不明确,为此本文将在考虑轴瓦开槽情况下,运用有限差分法求解Reynolds方程,研究凹槽对油膜承载力、轴心位置和端泄流量的影响。
1 理论建模
1.1 无量纲Reynolds方程
滑动轴承截面如图1所示,轴颈中心O1在外力Fl作用下相对于轴承中心O的某一偏心位置上转动,θ为偏位角。油膜最小厚度hmin=c-e和最大厚度hmax=c+e处于连心线OO1的延长线上,其中e为偏心距,c为半径间隙,c=R-r,R为轴承内孔半径,r为轴颈半径。沿着轴颈旋转速度ω方向,从hmax到hmin的半圈范围内,油膜收敛区呈现由大变小的收敛楔形,这是润滑油膜产生压力以承受外力的几何条件。定义两个坐标系:1) 静坐标以轴承垂直正上方为起始边,顺时针方向为正方向,用α表示转角。2) 动坐标以最大油膜厚度处为起始边,顺时针方向为正方向,用φ表示转角。
对于不可压缩液体动压润滑、处于稳定载荷下、有限宽滑动轴承的Reynolds方程为[5]:
(1)
其中:h为油膜厚度,h=c+e·cos(φ);p为油膜压力;μ为润滑油黏度;x为圆周方向坐标;z为轴向方向坐标;V为轴颈表面线速度,V=ωr。
为便于求解和推广应用,需要将Reynolds方程化为无量纲形式。分别对式(1)的x、z、h、p进行无量纲化,可得Reynolds方程无量纲形式:
(2)
其中:H=1+εcos(φ),ε为偏心率,ε=e/c,φ=x/r;λ=z/(B/2),B为轴承宽度。由式(2)可知,滑动轴承的油膜压力分布及润滑性能,取决于d/B和ε,d为轴颈直径。
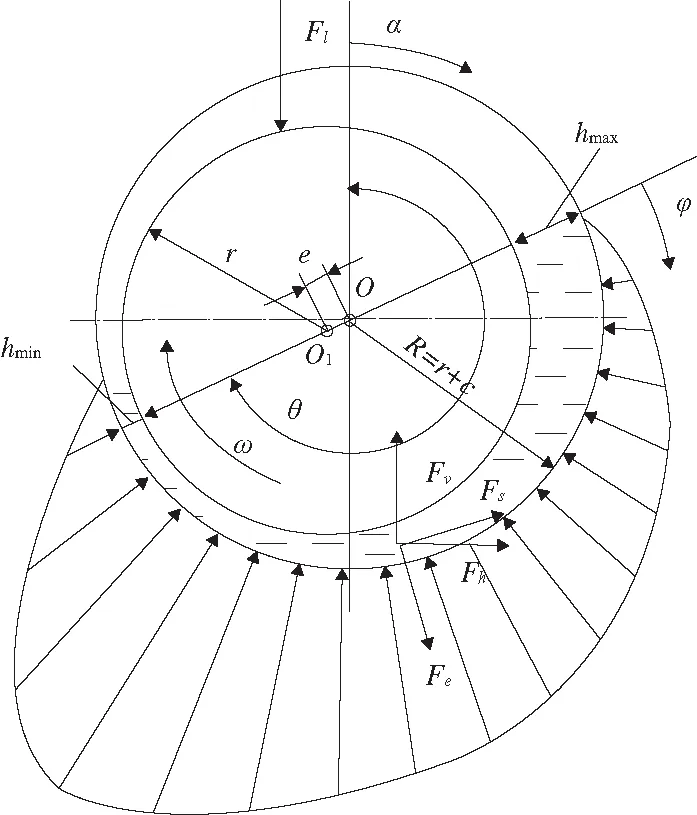
图1 滑动轴承截面示意图
1.2 数值求解过程
如图2所示,将滑动轴承内孔表面沿着圆周方向展开进行划分网格,圆周方向φ划分成m格,步长(每格宽度)为Δφ=2π/m;轴向方向λ划分成n格,步长为Δλ=2/n;用(i,j)表示每个节点位置,Pi,j表示该节点压力。
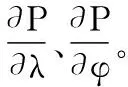
(3)
(4)
Ui,jPi+1,j+Vi,jPi-1,j+Wi,jPi,j+1+Ri,jPi,j-1-Si,jPi,j=Ti,j
(5)
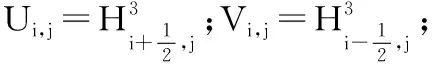
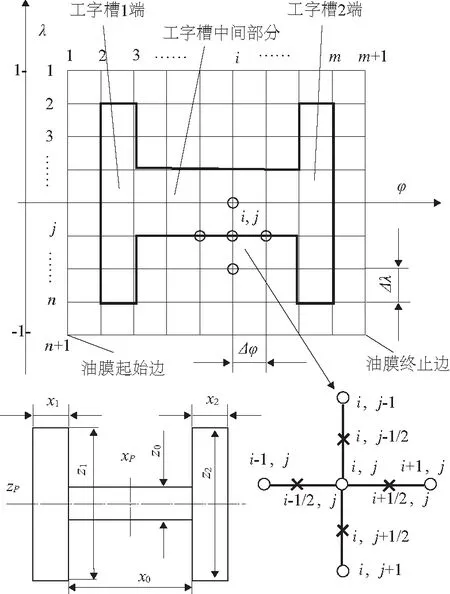
图2 轴瓦开槽时轴承内孔表面划分网格
当轴瓦上开有工字槽时,油膜收敛区相对于油槽的位置是随偏位角不断变化的,在数值求解时要考虑两者的相对位置关系。工字槽以圆周与轴向方向的中心线Xp、Zp来定位,Xp、Zp均以静坐标为参考。油膜收敛区圆周方向以最大油膜厚度处来定位,静坐标为参考坐标,轴向方向以轴承轴向中心位置来定位。流体的动压润滑效应在油膜厚度处于微米量级时表现的比较明显,工程实际中,凹槽深度远大于微米量级,此时凹槽对油膜压力的影响增强,凹槽内部压力等于供油压力量级。
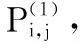
(6)
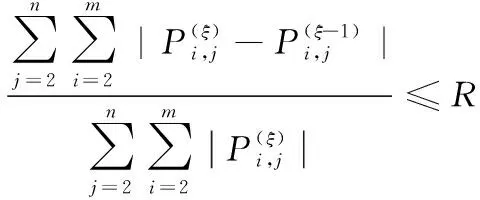
(7)
1.3 Reynolds边界条件
油膜自然破裂边界位于最小油膜厚度hmin之后的某个位置φ2处,在数值求解过程中,当计算出某节点Pi,j为负时,则取为0,并以此点作为该行上破裂边界近似位置,经过ξ次迭代后,破裂边界就会逐渐向自然破裂边界逼近[7-8]。
油膜起始点:φ=φ1=0,P=0;
油膜收敛区:φ1<φ<φ2,P=P(φ);
1.4 油膜力的计算
滑动轴承油膜水平分力Fh(无量纲)和垂直分力Fv(无量纲)计算公式如下,规定正方向:Fh水平向右,Fv垂直向上。
(8)
(9)
其中:fh为油膜水平分力,fv为油膜垂直分力。
根据Fh和Fv,可以计算出油膜承载力F(N):
(10)
1.5 偏位角θ、偏心率ε的修正
轴在转动过程中受外力作用,需要编制程序寻找油膜承载力与外力平衡时的轴心位置,即计算出平衡时偏位角和偏心率。定义外力方向角为θf,以静坐标为参考。由于油压峰值区位于最小油膜厚度附近,因此,将θf作为初始偏位角。将初始偏位角下不同偏心率时的油膜承载力F与外力Fl进行差值比较来确定初始偏心率,这样可以提高寻找效率。
具体修正方法:将F分解成沿着偏心距e方向的径向分力Fe和沿垂直于偏心距方向的切向分力Fs;同理,将Fl沿相同的两个方向分解成Fle和Fls;然后计算两个方向合力的算术平方根Ftot:
(11)
考虑到偏位角θ、偏心率ε变化均会影响到Ftot,所以同时调整θ和ε,粗调步长如式(12)、式(13),θ最大变化±1°,ε最大变化±0.01。
(12)
(13)
精调步长如式(14)和式(15),θ最大变化±0.1°,ε最大变化±0.001。
(14)
(15)
根据如下平衡条件,判定F与Fl是否平衡和终止搜索程序,T为相对平衡容差。
(16)
1.6 流量的计算
轴在转动过程中的旋转压力会引起轴承两端的润滑油端泄流量。为了指导应向轴承不断补充的供油量以保证润滑油填满收敛楔形间隙,需计算这些流量,计算公式如下:
(17)
(18)
其中:Q1、Q2分别为轴承两端的润滑油端泄流量(无量纲)。则总润滑油端泄油量Q(m3/s)计算公式为:
Q=(Q1+Q2)R3cω/6B)
(19)
2 计算结果与分析
2.1 轴瓦开槽对油膜承载力的影响
考虑到在轴向上凹槽宽度是与轴承宽度成正比例关系以及根据机械设计手册对于动压润滑滑动轴承宽径比的设计规范,采用3组不同宽径比B/d=6/16、12/16、16/16的有限宽滑动轴承,对比在轴瓦开槽和轴瓦无槽两种情况下对轴承工作性能的影响,轴承及相关参数如表1。考虑到凹槽深度大于微米量级时,凹槽内部油膜压力等于供油压力量级,本文采用的凹槽深度处于毫米量级,工字槽参数如表2。

表2 工字槽参数
图3是偏位角θ=100°时,滑动轴承轴瓦开槽与轴瓦无槽时油膜承载力的变化曲线。当宽径比相同,轴瓦开槽比无槽时油膜承载力有所下降,且随着偏心率的增大,降幅不断增大。这是由于此时油槽处于油膜收敛区,槽内部油膜厚度远大于其他位置,使得槽内部流体动压润滑效果不明显,且随着偏心率增大,收敛楔形间隙在不断增大,油槽对油压峰值区影响程度也越大。
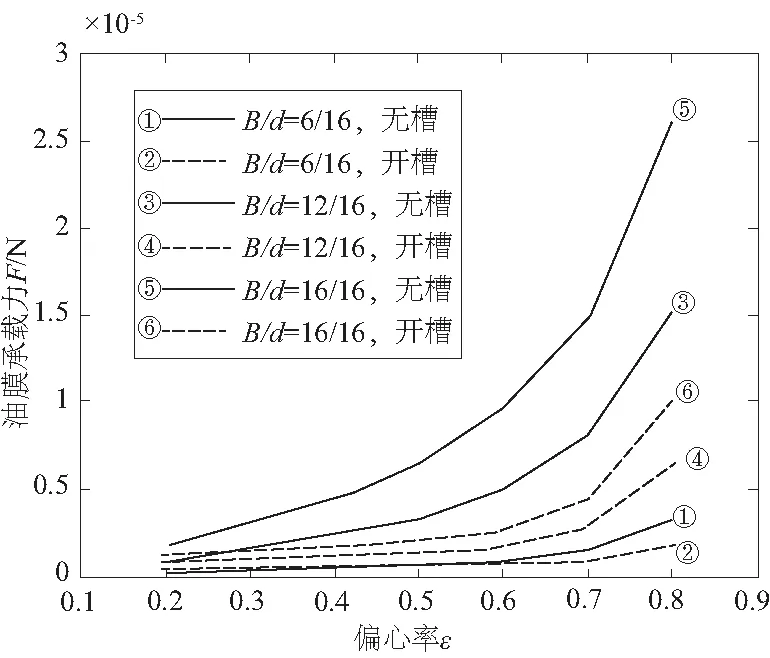
图3 油膜承载力变化曲线
当偏心率相同时,轴瓦开槽的油膜承载力与无槽相比有所下降,且随着宽径比的增加,降幅不断地增大。这是由于工字槽轴向宽度随着轴承宽径比的增加而不断增大,即油槽穿过油压峰值区域会不断增大,对峰值区油压影响程度也就越大。
不同偏心率和不同宽径比时油膜承载力变化情况如表3和表4所示。可以看出:小偏心率和宽径比时,油槽对油膜承载力影响不是特别明显;当偏心率>0.5,宽径比>12/16时,油槽对油膜承载力影响较大,降幅均达到50%以上。
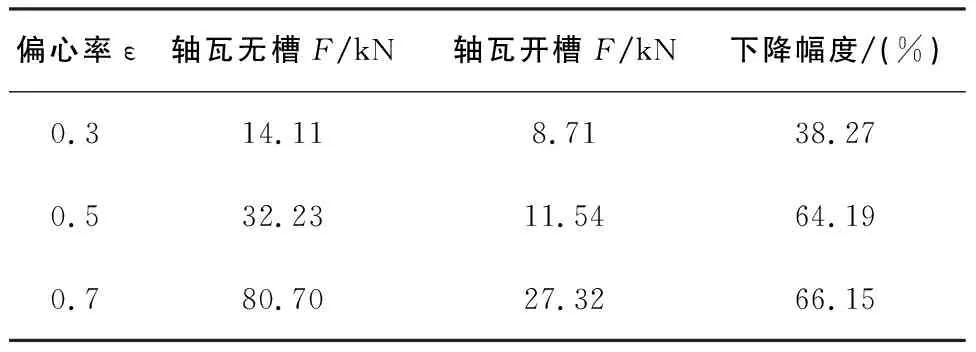
表3 B/d=12/16,不同偏心率时油膜承载力
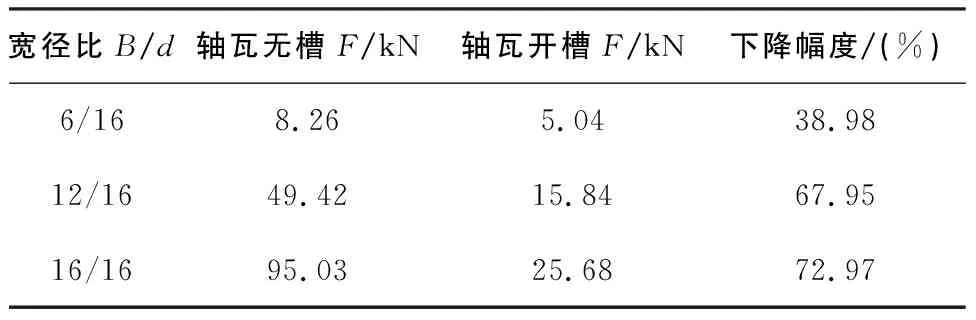
表4 ε=0.6,不同宽径比时油膜承载力
图4和图5是当B/d=12/16,ε=0.6时,轴瓦无槽与开槽时在动坐标下的油压分布。轴瓦无槽时,处于油膜收敛区的油压逐渐上升并在最小油膜厚度hmin处达到最大值,随后润滑油进入油膜扩散区,油压迅速降低,并在某一转角φ2处油膜破裂。轴瓦开槽时,油槽位于油膜收敛区,槽内油压接近供油压力Ps,收敛区油压普遍低于无槽时油膜压力,且峰值区油压大小和分布受油槽影响较大。
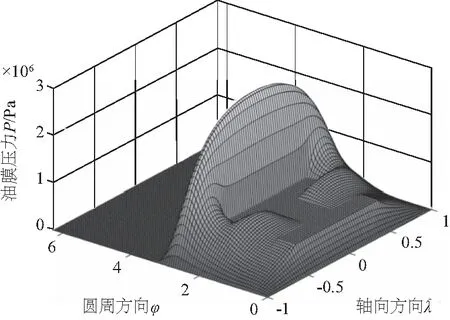
图4 轴瓦开槽时油膜压力分布
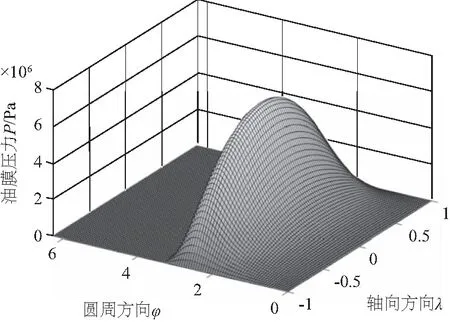
图5 轴瓦无槽时油膜压力分布
2.2 平衡时轴心位置及端泄油量的计算
在外力Fl=800 0N,外力方向角θf=180°,即外力方向垂直向下,轴承宽径比B/d=6/16,轴颈转速ω=600r/min时,运用前述偏位角、偏心率修正方法,寻找平衡时轴心位置。
在初始θ=θf时,由图6差值分析可得,ε=0.6为程序搜索初始偏心率。轴心位置搜索过程如图7所示,从中可知,平衡时的轴心位置为θ=228.1°,ε=0.689,当外力受到的扰动变化较小时,轴在平衡轴心位置附近稳定运行。采用修正的初始偏位角和偏心率的程序,与未进行差值修正相比(初始θ=60°,ε=0.5),寻找过程极大地缩短了。
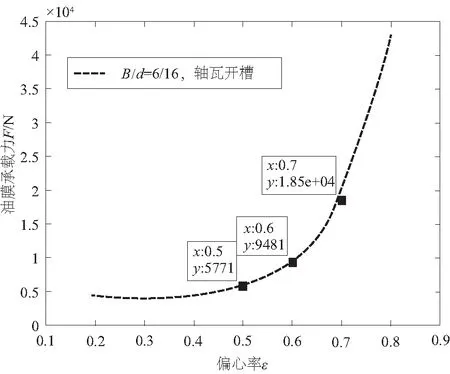
图6 B/d=6/16,油膜承载力随偏心率变化的曲线
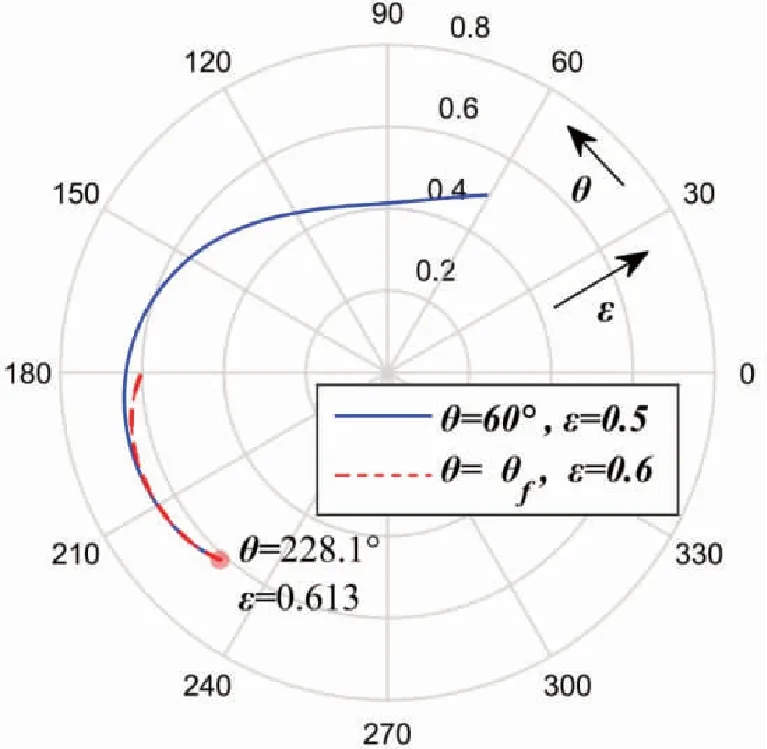
图7 平衡时的轴心位置搜索图
平衡时油压分布如图8所示,可以看出,平衡时油槽大部分位于油膜扩散区,对油膜收敛区油压分布影响较小,此时收敛区油压分布规律接近轴瓦无槽时油压分布。
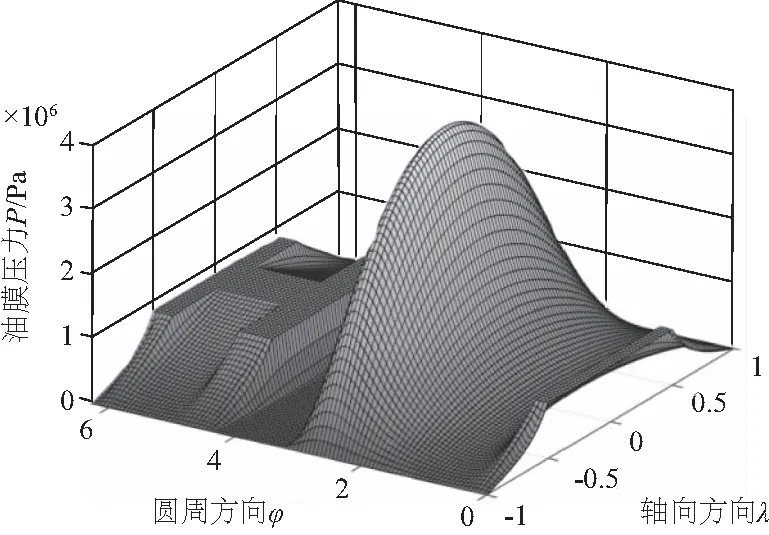
图8 平衡时油膜压力分布
在上述工况及轴心位置下,不同转速ω=600~1 800r/min时润滑油端泄油量变化曲线如图9所示。可以看出,随着转速增大,润滑油端泄流量呈现上升趋势,且轴瓦开槽比无槽时端泄流量有所增加,这是由于位于油膜扩散区的油槽在轴向两端的压力梯度影响。
3 结语
1) 当油槽位于油膜收敛区时,收敛区油压分布受油槽影响较大,且轴瓦开槽比无槽时油膜承载力要有所下降,且随着偏心率和宽径比的增大,降幅在不断增大。
2) 编制的轴心位置搜索程序,将外力方向角作为初始偏位角,由差值分析得到初始偏心率,可以缩短寻找平衡时轴心位置过程。平衡时,随着转速的增大,润滑油端泄流量呈现上升趋势。
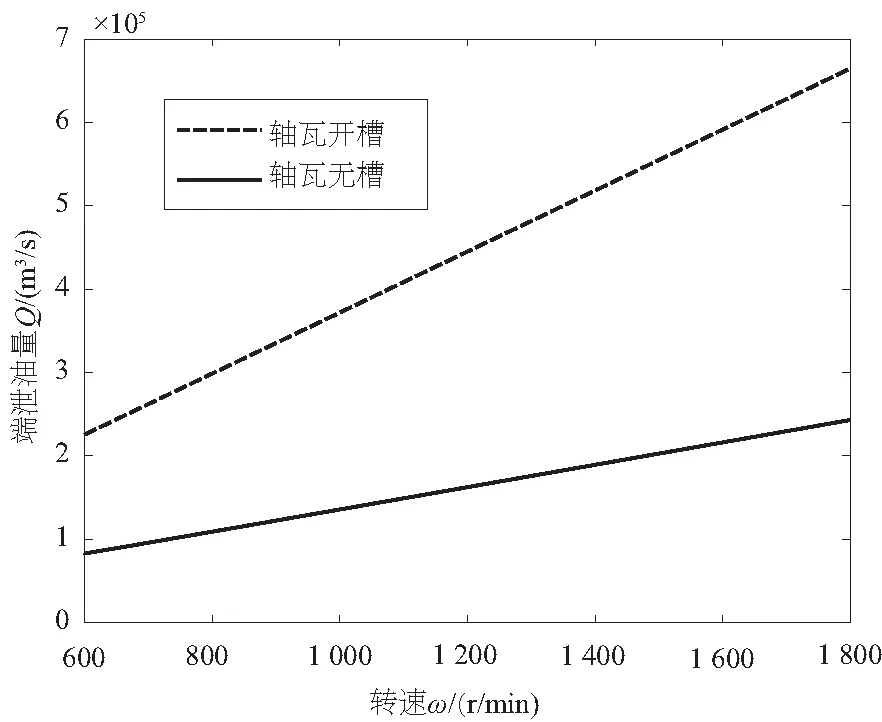
图9 端泄流量随转速变化的曲线
应该指出,对于轴瓦开有多槽形式,主要是考虑多槽在轴承圆周方向不同角度的布置对轴承工作性能的影响,本文的后续工作将陆续展开。
