航空发动机齿轮传动系统轴承受力与发热量一体化计算

巢青，钟易成，汪元林，陈进

(1. 中航工业系统有限公司，北京 100000； 2. 南京航空航天大学，江苏 南京 210016；3. 南京普国科技有限公司，江苏 南京 210016)

0 引言

对于航空发动机，滑油系统的合理、稳定、可靠是保证其传动系统乃至整机稳定、可靠的重要条件[1]。而滑油系统的设计、评估、优化等又必须基于传动系统各部件的受力和发热量[2]。可见，传动系统部件的受力和发热量计算对滑油系统乃至发动机整机的稳定、可靠都不可或缺[3]。

基于上述背景，为了计算某型航空发动机的某齿轮传动腔室内轴承的受力和发热量，为其滑油系统的评估和优化改进提供依据，本文在相关已有研究成果[4-6]的基础上，综合运用运动学、动力学以及热力学等有关理论，分析了轴承的负荷来源，总结、推导了各类轴承的受力和发热量计算式，在此基础上，利用C++语言开发了航空发动机齿轮传动系统轴承受力发热量一体化计算程序并进行了计算分析。

1 齿轮和轴承的受力计算

航空发动机齿轮传动系统主要由传动轴、轴承和齿轮组成。轴承在高速转动过程中支承传动轴工作，传动轴上齿轮在啮合传动过程中产生的各向分力经轴传递到轴承处，由轴承支反力抵消。也就是说，轴承的负荷来自齿轮的啮合传动，因此，进行轴承受力计算就必须要输入齿轮的受力。

1.1 齿轮受力计算

直齿圆柱齿轮啮合时的受力示意如图1所示，啮合点法向力在切向和径向两个方向存在分力，即法向力是二维力。斜齿圆柱齿轮啮合时的受力示意如图2所示，啮合点法向力在切向、径向和轴向3个方向存在分力，即法向力是三维力。锥齿轮(包括直齿锥齿轮和弧齿锥齿轮)啮合时的受力示意如图3和图4所示，由于结构特殊，啮合点法向力也是三维力。

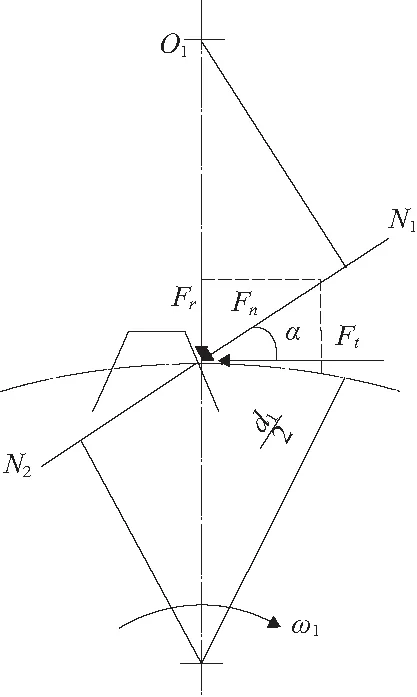
图1 直齿圆柱齿轮啮合点受力示意图

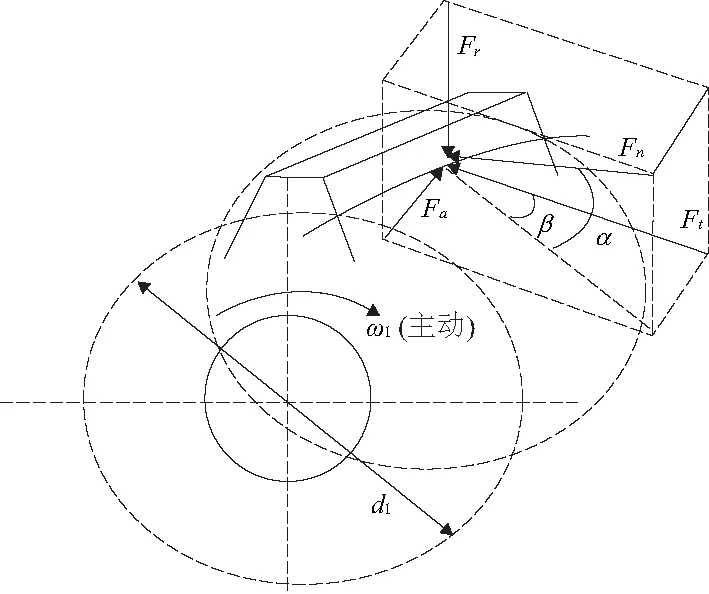
图2 斜齿圆柱齿轮啮合点受力示意图

图4 弧齿锥齿轮啮合点受力示意图

在转速和功率已知的条件下，齿轮的转矩可由下式计算：

T=9.55×106P/n

式中：T为齿轮转矩，单位N·m；P为齿轮功率，单位W；n为齿轮转速，单位r/min。

对于直齿圆柱齿轮，径向力Fr、切向力Ft和法向力Fn由式(1)计算。

(1)

对于斜齿圆柱齿轮，轴向力Fa、径向力Fr、切向力Ft和法向力Fn由式(2)计算。

(2)

对于直齿锥齿轮，轴向力Fa、径向力Fr、切向力Ft和法向力Fn由式(3)计算[7]。

(3)

对于弧齿锥齿轮，轴向力Fa、径向力Fr、切向力Ft和法向力Fn由式(4)计算[8]。

(4)

式(1)-式(4)各参数名称汇总见表1。

表1 齿轮受力计算式参数名称汇总表

1.2 轴承径向力计算

在齿轮所受各向分力已知的条件下，本文分两轴承轴系和三轴承轴系两种情况进行轴承径向力的计算。

1) 两轴承轴系

两轴承轴系中，两轴承构成简支梁结构，轴承径向力计算模型如图5所示。

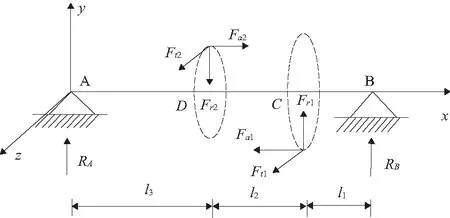
图5 两轴承轴系轴承径向力计算模型

此时，对支点B建立力矩方程式(5)即可求出轴承A的径向力RA。

RAl-Fr2(l1+l2)+Fr1l1+Fa2r2+Fa1r1=0

(5)

由于整个轴系y方向合力为0，因此，利用式(6)求出轴承B的径向力RB。

RB+RA-Fr2+Fr1=0

(6)

2) 三轴承轴系

对于三轴承轴系的情况，建立轴承径向力计算模型如图6所示。

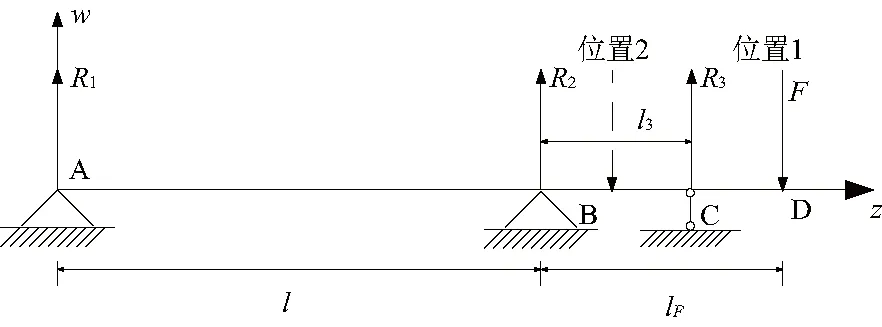
图6 三轴承轴系轴承径向力计算模型

齿轮位于位置1时，假想将轴承C去掉，以支反力R3代替其作用，便可建立如图7所示的齿轮径向F单独作用下的静定梁模型和载荷R3单独作用下的静定梁模型。根据C处挠度为0，可建立挠度平衡方程。

图7 静定简支梁与静定悬臂梁模型

如果齿轮在啮合点处存在轴向力，力作用线平行于轴中心线，但与轴线间存在偏心距，此时，轴向力会产生一个偏心力矩，从而会引起C截面产生附加挠度。偏心力矩作用下悬臂梁弯曲示意图如图8所示。

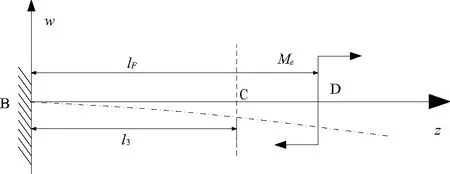
图8 偏心力矩作用下悬臂梁弯曲示意图

将轴向力引起的附加挠度带入之前建立的挠度平衡方程，即可求得轴承C的径向力：

求得R3后，其余两个轴承的径向力便可由两轴承简支梁模型进行求解。

齿轮位于位置2时，计算方法同上，可求得轴承C径向力:

求得R3后，其余两个轴承的径向力同样根据两轴承简支梁模型进行求解。

1.3 轴承轴向力计算

在齿轮所受各向分力已知的条件下，轴承轴向力由轴承类型、支承形式和安装方式等因素决定，根据已有文献，总结计算方法[7],[11-13]简述如下：

a) 圆柱滚子轴承不承受轴向力。

b) 对于角接触球轴承，计算步骤为：

寓言一般篇幅短小，语言凝练，常常蕴深刻哲理于浅显语言和生动故事中。寓言结构简单却富有表现力，一般具有明显的讽喻性和教育性，常用比喻、夸张、象征等修辞手法。它的故事情节多为虚构，主角多是人格化了的动物、植物或者自然界的其他事物。

1) 根据结构图判断轴承的安装方式；

2) 画出轴承受力简图；

3) 确定轴承内部轴向力的大小和方向；

4) 确定作用于传动轴上的轴向外负荷的合力大小和方向；

5) 判明轴上全部轴向负荷(包括轴向外负荷和轴承内部轴向力)的合力指向，确定“压紧”轴承和“放松”轴承；

6) “压紧”轴承所受轴向力等于除本身内部轴向力以外的其他所有轴向负荷的代数和(即另一个轴承的内部轴向力与外负荷的代数和)；

7) “放松”轴承所受轴向力等于轴承自身的内部轴向力。

c) 止推轴承承受轴上所有轴向载荷。

在后续的程序开发过程中，将直接引用文献中的有关计算式。

2 轴承发热量计算

2.1 中低速轴承发热量计算

中低速轴承的发热量采用功率损失模型进行计算[9]，功率H由力矩M和角速度ω决定，其关系式为：

H=0.001 M·ω=1.047×10-4M·n

式中：n为转速，单位r/min。

Palmgren通过试验总结得到中低速球轴承摩擦力矩计算式[12]如下：

式中：Ml为由载荷引起的摩擦力矩；Mv为由润滑剂粘性引起的摩擦力矩；f1是一个与轴承结构和载荷有关的系数，P1取决于轴承载荷的大小和方向，它们的计算方法可以从文献[9] 中的表格查得；dm为轴承节圆直径；v为润滑油运动粘度；f0是一个与轴承类型和润滑方式有关的系数，其值也可以从文献[9] 中的表格查得。

相较于球轴承，圆柱滚子轴承的摩擦力矩多出一项滚子端面和挡边之间的摩擦力矩Mf。

Mf=ffFadm

式中：ff为端面和挡边之间的摩擦系数；Fa为轴承轴向力。

2.2 高速轴承发热量计算

对于高速球轴承，其发热量用下式计算[10]：

对于高速圆柱滚子轴承，其发热量用下式计算[10]：

式中各参数名称汇总见表2。

表2 发热量计算参数名称汇总表

2.3 高速轴承判定

高速轴承的判定依据是轴承的DN值，如：

DN=di×n>0.6×106mm·r/min

或：

DN=dm×n>1.0×106mm·r/min

则该轴承为高速轴承。

式中：di为轴承内径，dm为轴承节圆直径。

3 轴承受力发热量一体化计算程序

程序开发总体思路如图9所示。程序的输入参数有传动轴上齿轮轴承部件的几何参数、位置参数、传动轴-齿轮-轴承之间的拓扑关系以及齿轮的转速和功率。程序根据部件类型标志识别各个部件，读入参数后自动进行计算。

图9 程序开发总体思路简图

程序分为3个功能模块，如图10所示。3个功能模块之间相互不独立，齿轮与轴承的受力计算存在逻辑先后关系，齿轮受力计算完成后，其结果是轴承受力计算的输入，轴承受力计算结果是轴承发热量计算的输入，各功能模块输入输出关系如图11所示。

图10 程序功能模块示意图

图11 功能模块输入输出示意图

程序编译并链接成功后生成控制台程序即运行软件。使用时，导入齿轮、轴承参数输入文件，程序自动进行轴承受力与发热量计算，计算完成后输出结果文件。

4 轴承受力发热量一体化计算

某型航空发动机的某齿轮传动腔室的传动系统简图如图12所示，现计算额定转速工况下各轴承的受力和发热量。

图12 腔室传动系统简图

该传动系统总共5个轴承，3个齿轮，形成2个齿轮副，拓扑关系如图13所示。

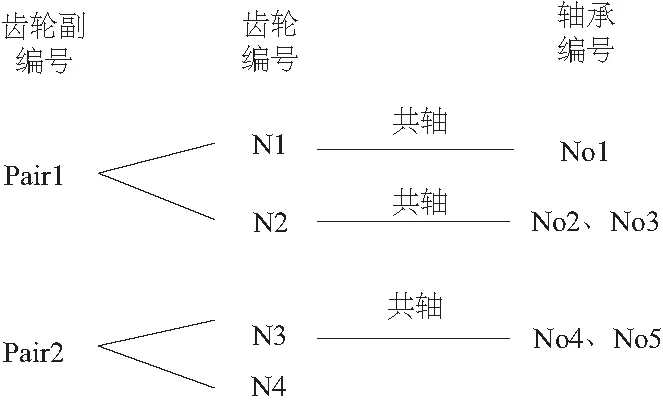
图13 传动系统拓扑关系简图

4.1 齿轮输入参数

齿轮输入参数汇总见表3。

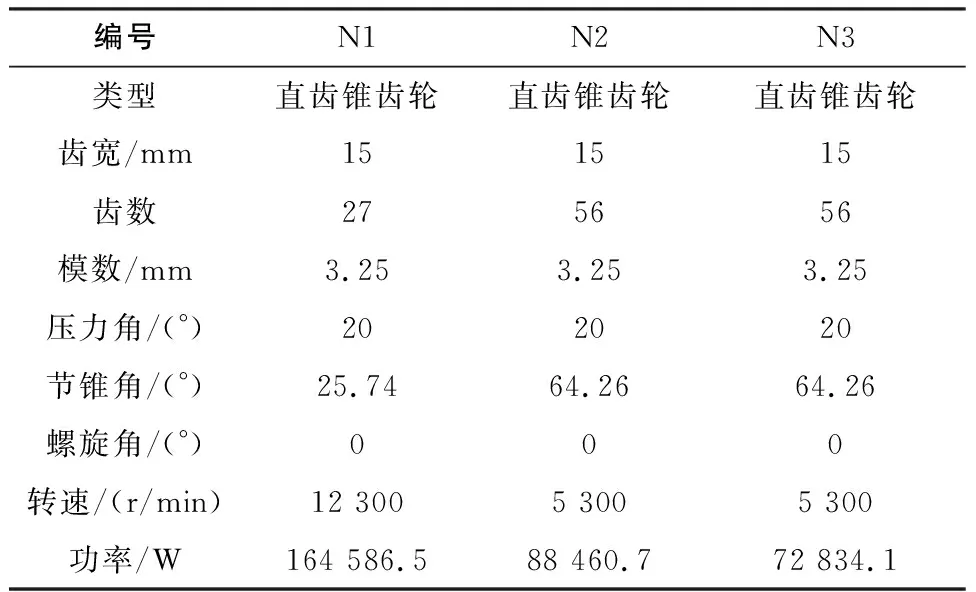
表3 齿轮输入参数汇总表

4.2 轴承输入参数

轴承输入参数汇总见表4。

表4 轴承输入参数汇总表

4.3 计算结果

轴承所受径向力和轴向力计算结果分别汇总见表5和表6。

表5 轴承径向力计算结果汇总表 N

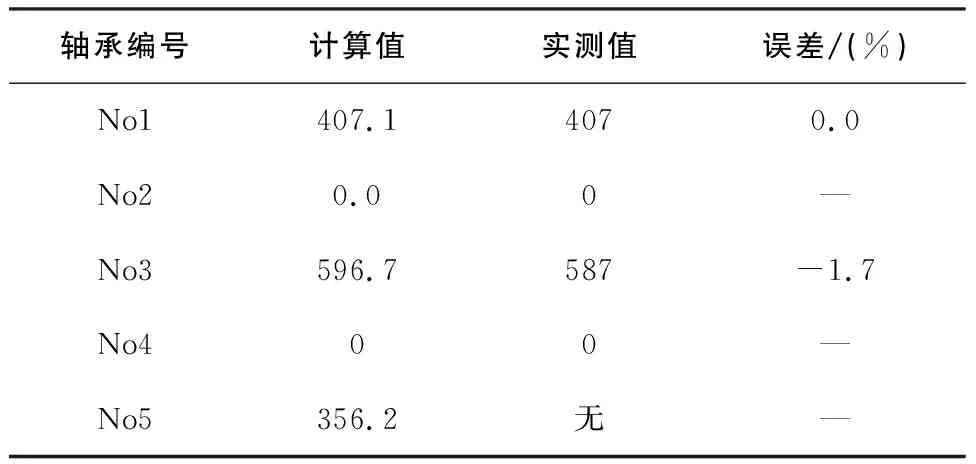
表6 轴承轴向力计算结果汇总表 N

由表可见：1) 整体来看，No3轴承受力最大，No5轴承受力最小；2) 软件计算结果与实测值相差很小，最大误差仅3.2%，表明程序采用的力学计算模型合理，计算结果可靠。

轴承发热量计算结果如图14所示。

图14 轴承发热量计算结果(单位：W)

从计算结果看：No1轴承发热量最大，达到315.6W，No5轴承发热量最小，为71.9W；No2、No3和No4轴承的发热量接近。

对于其他工况条件，仅需更改齿轮输入文件中的转速和功率值即可快速计算得到各轴承的受力和发热量。

5 结语

利用开发的航空发动机齿轮传动系统轴承受力发热一体化计算程序计算了某型航空发动机的某齿轮传动腔室中的轴承受力和发热量，所得主要结论如下：

1) 关于轴承受力，程序计算结果与实测值基本一致，表明程序采用的力学计算模型合理，计算结果可靠。

2) 额定转速工况下，该传动腔室中的No1轴承发热量最大，达到315.6W，工作中需要特别注意对它的润滑冷却。