正交并联六轴力传感器耦合误差测量模型及实验分析

2019-01-08赵铁石赵延治胡强强冀文杰

中国机械工程 2018年24期

牛智赵铁石赵延治胡强强冀文杰

1.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，066004 2.先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛，066004

0 引言

六轴力传感器是一种能够测量广义外力全力信息的传感器，广泛应用于机器人、航空航天等领域。许多学者在六轴力传感器结构设计方面开展了工作。GAO等[1]采用弹性球铰替代传统球面副，设计了微型六轴力/力矩传感器；刘俊等[2]研制了一种平板式压电六轴力/力矩传感器；还有众多国内外学者开展了并联六轴力传感器研究[3-4]。正交并联六轴力传感器是在并联六轴力传感器基础上进行改进的一种传感器，具有承载力大、解耦性能良好等特点。WRIGHT等[5]设计了一种正交六轴力传感器并应用于火箭推力实验。赵延治等[6]提出了一种正交自标定六轴力传感器。

随着机器人、航空航天等领域的高速发展，这些领域对重载高精度六轴力传感器的需求逐渐增加。但是很多因素(如干扰力、维间耦合等)会使并联六轴力传感器存在较大误差。许多学者针对六轴力传感器的误差与精度开展了研究。侯雨雷等[7]对预紧式并联六轴力传感器位姿误差进行了分析；孙立广等[8]通过对新型六轴力传感器标定系统进行建模与误差分析来提高六轴力传感器精度；姚建涛等[9]针对一种预紧式超静定Stewart 结构六轴力传感器，分析了传感器的误差；贾振元等[10]基于Stewart结构六轴大力传感器的性能、误差等进行了分析及结构优化；龚莉杰等[11]设计了一种全平面型六轴力/力矩传感器，采用最小二乘法对传感器弹性体进行解耦标定，以提高测量精度；王志军等[12-13]针对一种预紧式并联六轴力传感器，分析了预紧力对传感器误差的影响；干方建等[14]探讨了传感器的动态设计问题,并分析了传感器维间耦合的本质关系；朱文超等[15]提出一种滤波算法来提高六轴力传感器测量精度的方法。

对于正交并联六轴力传感器，构型上的变化使得其分支间摩擦造成的耦合误差输出产生了新特点，这些因素会影响测量精度。本文考虑测量分支间摩擦及正交结构自身特点引起的耦合误差输出，建立考虑两种耦合误差因素下的测量模型，分析探讨传感器分支刚度、尺寸、轴向力大小等参数与两种耦合误差输出之间的影响关系，据此优化上述参数，研制了一种正交并联六轴力传感器并进行了实验以验证其测量精度。

1 测量原理与传感器结构

1.1 传感器结构

基于并联六轴力传感器所设计的正交并联六轴力传感器结构见图1。传感器主要由两类测力分支构成：一类为垂向分支，另一类为水平分支。

传感器的水平测力分支及垂向分支中轮辐式力传感器两侧设计有球解耦结构，通过球解耦结构与力传感器相接触来进行测力，对于球解耦结构，设计有定位调节装置来保证球解耦结构的位置调节，同时有调节预紧装置，在传感器非工作状态下可通过调节预紧装置，使得球解耦结构与力传感器脱离接触，在工作状态下通过调节预紧装置使得水平分支进入测量状态。同时，垂向分支的压盖可调节上平台在4个支撑点的高度。

正交并联六轴力传感器结构简图见图2。图2中，标号1～8即8个测力分支。在测力台的底面分布4个垂向测力分支，4个侧面分布4个水平测力分支。A1～A4为垂向分支与固定部位的连接点，B1～B4为垂向分支与测力台的连接点，A5～A8及B5～B8为水平分支与测力板的连接点。

图2 正交并联六轴力传感器结构简图Fig.2 Structure diagram of sensor

1.2 传感器测量原理

参考图2以及根据螺旋理论，传感器测量原理为

F=Gf

(1)

式(1)为六轴力传感器具有一般性的理论测量模型，F为广义外力，f为六轴力传感器分支测量力，G表示两者之间的静力影响系数，即

(2)

对于式(2)中各项，有

Si=(lOBi-lOAi)/|lOBi-lOAi|

SOi=(lOBi×lOAi)/|lOBi-lOAi|

其中，lOAi、lOBi分别表示Ai点、Bi点到坐标中心O的位置矢量，设各点坐标分别为Ai=(xai，yai，zai)，Bi=(xbi，ybi，zbi)，则有

由高等空间机构学可知：Si为第i分支方向矢量，SOi为Si对原点O的线矩。图2中，各垂向分支之间的垂直间距为lv，水平分支之间的垂直间距为lh,则式(2)矩阵的具体表达式为

(3)

2 测量模型的建立

六轴力传感器通过分布在各分支的轮辐式力传感器来测量所受的广义外力。在测量过程中，摩擦力的存在会产生误差，同时，由于正交构型并联六轴力传感器自身结构特点，也会在测量力矩时产生耦合输出，这些因素对六轴力传感器的影响转化为实际测量分支所测得的力与实际所受力之间存在的误差δf。可得

F=G(f+δf)

(4)

2.1 摩擦耦合输出分析

误差δf受到分支间存在的摩擦的影响，而摩擦所造成的力也难以测量得到，由此通过对所设计的六轴力传感器分支进行受力分析，建立考虑其分支滚动摩擦时摩擦力与测力分支所受轴向力的关系。当六轴力传感器测力台受到广义外力时，传感器测力分支中的钢球受力见图3。

图3 测量分支受力分析简图Fig.3 Force analysis of measurement branch

(5)

同时设钢球直径为l, 则有

Mf1+Mf2=1fl=2fl

(6)

轴向力f1、f2两者数值上相等，故将两者统一表示为fi(i表示传感器分支编号，用来表示第i个分支的轴向力)，同理可将摩擦力1f、2f统一表示为σfi(i表示传感器分支编号，用来表示第i个分支的摩擦力)。最终根据式(5)、式(6)可得

(7)

当一个分支的钢球受力时，摩擦力与分支所受轴向力的关系即式(7)。

单个分支受力时的分析见上文。由图2中分支编号及传感器结构可知，当传感器受到广义外力时，例如在x方向上受力，5、7号分支进行测量，而1～4号及6、8号分支会产生摩擦力，故将某个方向的测量分支称为“方向测量分支”，产生摩擦力的分支称为“耦合摩擦分支”。

2.2 水平分支耦合输出分析

正交并联六轴力传感器由于自身结构特点,还会产生一种特有的耦合输出。根据所设计的六轴力传感器及水平测力分支的结构，当传感器测力台发生绕x轴或y轴方向翻转时，对应水平测力分支上模块会随着测力台一起翻转，见图4。水平测力分支上模块会随着测力部位翻转产生变形，从而造成一种新的耦合输出。在实际中，传感器主要靠测力分支的变形来进行测力，故在设计及制造中，测力台的刚度远大于测力分支的刚度，测力台产生的挠度变形相对于分支变形来说很小，将测力台作为刚体考虑，测力台只产生很微小的θ转角翻转，其挠度变形可忽略。

图4 水平分支测量耦合输出示意图Fig.4 Measurement coupling output of horizontal branch

图4中，当垂向分支受到力时产生变形Δz，则测力台会产生转角θ，测力板的长度为L，则垂向分支的变形Δz=0.5Lsinθ。此时，如果没有水平分支下模块钢球的阻挡，则水平分支上模块会随着测力台产生θ角度的翻转，水平分支翻转造成的钢球接触点位移Δx为c点到a点的垂直距离，Δx可分成两部分求出：b点到a点的垂直距离设为Δx1，c点到b点的垂直距离为Δx2(因为b点与a点接近，难以在图4中区分出这段距离，所以未在图4中标出)。p为水平测量分支上模块的宽度；q为b点到c点的距离，为钢球接触点位置的距离；o点为水平分支的转动中心。可知Δx1可由oa的长度与ob乘以θ角度余弦值的积做差得到，Δx2可由bc的长度乘以θ角度正弦值得到，则有

总变形量

(8)

(9)

式中，ki为产生变形的第i水平分支的轴向刚度。

再依据垂向分支的变形Δz=0.5Lsinθ，得到

fj2=kj2Δz=0.5kj2Lsinθ

(10)

(11)

(12)

2.3 综合误差

F=G′f+C3=(G+G1+G2)f+C3

(13)

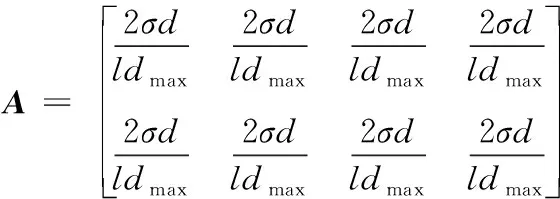
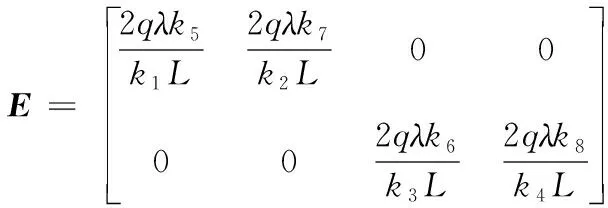
其中，O1为3×4零矩阵，O2为1×4零矩阵，O3为2×4零矩阵，O4为4×4零矩阵。式(13)即考虑了分支摩擦及水平分支耦合输出的测量模型表达式。

3 数值算例分析

3.1 传感器测量值数值算例

根据所建立的模型，设滚动摩阻系数σ=0.01 mm，钢球直径l=20 mm，d/dmax=0.5，p=60 mm，q=60 mm，L=1 m，λ=0.5，水平分支的刚度值为1.88×108m/N，垂向分支刚度值为4.88×108m/N，各方向加载一个从0～10 kN的力，各值代入式(13)可得到X测量方向上的测力分支理论测量值与考虑耦合的测量值曲线，见图5。由图5可以看出，两种耦合输出会造成实际测量值与理论测量值存在差异。

图5 理论测量值与考虑耦合测量值关系Fig.5 Relationship between theoretical measurement values and coupled measurement values

3.2 耦合误差与传感器参数数值算例分析

基于正交并联六轴力传感器的分析，当滚动摩阻系数σ=0.01 mm、每个产生摩擦的分支轴向力为5 kN时，对于传感器各分支产生的摩擦力，钢球直径l与d/dmax的比值对摩擦力的影响见图6。

由图6可以看出，随着钢球直径增大，摩擦力会减小；随着d/dmax增大，摩擦力会增大。摩擦力的变化受d/dmax变化的影响更大。

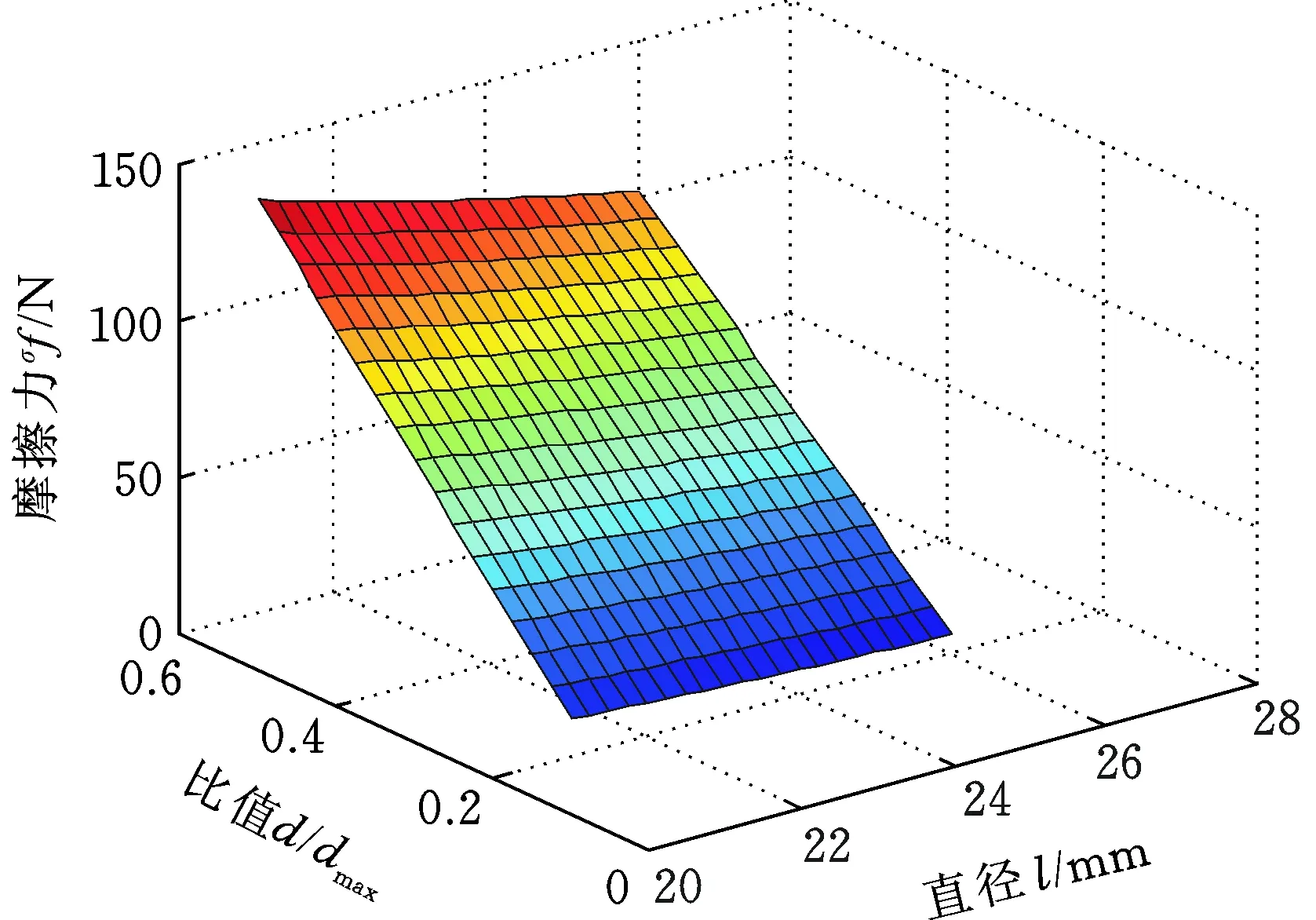
图6 钢球直径与中心距离比值对摩擦力的影响Fig.6 Influence of ball diameter and center distance on friction force

同理，对于水平分支耦合力，假设此时垂向分支受到方向相反的力5 kN，水平分支的刚度值为1.88×108m/N，垂向分支刚度值为4.88×108m/N，则钢球接触点位置距离q与测力台长度L对水平分支耦合输出的影响见图7。

图7 水平分支上模块接触点距离与测力台长度对受耦合力的影响Fig.7 Influence of module contact point distance and lengthof force measuring plate on coupling force

由图7可以看出，当竖直分支力为5 kN时，耦合输出随着钢球接触点位置距离q的增大而增大，随着L的增大而减小，q的变化对耦合输出影响更大。

当q=60 mm、测力台长度L=1 m时，水平分支刚度与垂向分支刚度对水平分支耦合输出的影响见图8。

图8 竖直测量分支刚度与水平分支刚度对受力的影响Fig.8 Influence of vertical branch stiffness and horizontal branch stiffness on coupling force

由图8可以看出，耦合输出随着水平分支刚度的增大而增大，随着垂向分支刚度的增大而减小，水平分支刚度的变化对耦合输出影响更大。

由图3～图8可知，在传感器受到广义力时，因为各分支间存在摩擦耦合作用，同时当传感器平台受到翻转力矩时，会对水平测量分支造成测量耦合误差输出，使得所加载力与理想模型存在偏差。其中，摩擦所造成的耦合误差受到相应测量方向上钢球直径、滚动摩阻的影响。而由翻转力矩所造成的水平分支耦合输出值则受到测力台长度、水平测量上模块的长度、上模块宽度、钢球接触点位置距离以及竖直分支刚度、水平分支刚度的影响。

综上所述，在设计正交并联六轴力传感器时，将滑动摩擦变为滚动摩擦，减小了摩擦耦合输出的同时，还应注意各水平、竖直分支的刚度以及测力台长度、水平模块的各项尺寸参数对耦合误差输出的影响。

4 传感器的标定实验与误差分布

根据前文依次设计了传感器及测力分支。测力分支所用钢球采用淬火钢球，并且在安装过程中涂抹润滑脂，以减小滚动摩阻系数，传感器测量分支所用材料为42CrMo并进行热处理，以提高垂向分支刚度减小测量时的形变。传感器竖直分支间的距离(测力台长度)会影响水平分支耦合输出，考虑到测量传感器各项同性指标，将六轴力传感器设计为边长为1.2 m的正方形(由前文可知，测力台长度增大会减小耦合输出，但是后续研究中欲将所设计传感器应用为人体生物测力台，还应考虑传感器实际使用安装场所条件，测力台长度不是越大越适合，故测力台长宽均设计为1.2 m)。水平分支上模块的高度需要尽量减小，以减小钢球接触点距离，但受到所用轮辐式力传感器尺寸限制，钢球接触点距离设计为60 mm。最终所设计的传感器及内部构成见图9。

图9 正交并联六轴力传感器及内部组成Fig.9 Orthogonal parallel six-axis force sensor and internal composition

组装完成的传感器外部安装不锈钢板并搭配一块可测人体脚部压力分布的测力板，可对人体进行受力测量。内部构成中，每个测力分支输出信号到数据采集仪表(数据采集仪表给测力分支中的轮辐式力传感器提供电压)之后由无线传输模块将数据传输到电脑中的采集程序。

4.1 正交并联六轴力传感器标定实验

将所加载的广义外力分为20个加载点进行加载，每次加载递增500 N，至满量程后再依次递减500 N后卸载为0。传感器标定实验见图10(为了实验方便，标定实验时传感器并未如图9组装完成)。

图10 正交并联六轴力传感器加载标定实验Fig.10 Load calibration experiment of sensor

传感器各分支输出曲线见图11。图11中，fi表示传感器第i号分支输出力值。

4.2 正交并联六轴力传感器误差分布

在六轴力传感器标定过程中，为了提高标定精度，通常所选取的标定力/力矩的数目大于6。此时，通过标定矩阵所标定的六轴力传感器存在误差矩阵H，存在关系类似式(1)：F6×n=G6×8·f8×n+E6×n，其中，F6×n为六轴力传感器受到的加载六轴力矩阵，每一列代表一个六轴力向量；G6×8为标定矩阵；f8×n为测力分支输出矩阵，每一列代表各分支的测量力值向量；

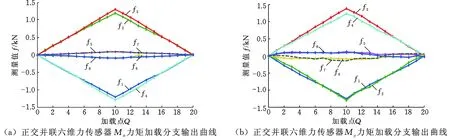
图11 加载标定实验分支输出曲线Fig.11 Branch output curves of the calibration experiment

E6×n为误差矩阵。而对于传感器误差矩阵，有

E=|FS-F|/FFS

其中，FS是实际施加的力/力矩矩阵，F是通过计算得到的力/力矩矩阵，FFS是各维力/力矩满量程值向量。基于对传感器的加载标定实验数据，求得标定矩阵G：

根据实验数据，求得传感器误差矩阵：

Err=

在六轴力传感器误差矩阵中，主对角线上元素表示该方向所加载的广义外力与所测量到的力最大相对误差。其他非主对角线上元素表示进行某个方向加载时其他方向上的耦合误差输出。如第一行第一列元素表示在Fx方向加载时，测量Fx加载力最大相对误差为0.43%；第二行第一列元素表示Fy方向加载时，Fx方向产生耦合输出误差为0.37%。由误差矩阵各误差值可以看出，所设计的传感器在10 kN量程范围内的最大测量误差为1.28%，最大耦合误差为1.98%。误差矩阵中X向力矩和Y向力矩加载时的耦合误差见图12。

图12 正交并联六轴力传感器II类误差分布Fig.12 Class error II distribution of the sensor

由图12a、图12b及误差矩阵值可以看出，当进行Mx向力矩加载时，Fy耦合误差输出略大于Fx；而进行My向力矩加载时，Fx耦合误差输出略大于Fy。其原因是除了摩擦耦合输出的影响，当进行Mx向力矩加载时，测量Fy方向水平分支会有翻转造成的耦合输出的影响。同理，进行My向力矩加载时，测量Fx方向水平分支会有翻转造成的耦合输出的影响。

4.3 测量精度验证实验

标定实验进行之后，为了验证所设计六轴力传感器测量精度，进行了应用实验以验证其精度，见图13。图13中测量了人前后脚站立于传感器上及在传感器上下蹲时的受力测量。传感器上搭配的测力板可测量垂向方向脚部压力分布值及受力面积，故可得到垂向方向的力与传感器测量值并进行对比验证。对比结果见表1。表1中，Fp为测力板所测得力，F为传感器所测得力，几种测量情况下的最大相对误差为0.67%。

通过验证实验及表1可以看出，所设计的传感器在测量大小为人体重力测量范围内具有较好测量精度。在实验中也发现，传感器搭配的数据采集系统采集频率过慢，故动态采集到的测量点过少，不能形成平滑曲线。后续将搭配高速采集设备，对人体动态测量展开研究。