基于无应力状态法的预应力混凝土斜拉桥合理成桥状态加速迭代收敛

张寅涛, 白 露

(中交第一公路勘察设计研究院有限公司, 陕西 西安 710068)

目前大跨度预应力混凝土斜拉桥梁(PC斜拉桥)多数采用分阶段成形的方式进行建造[1].PC斜拉桥在施工过程中结构体系的改变和施工荷载均会对结构受力产生影响,因此控制施工质量的好坏对于保证成桥状态结构内力和线形具有非常重要的意义[2-3].对于预应力混凝土斜拉桥,基于增量累加的传统施工控制分析方法(如正装迭代法、倒拆-正装迭代法等)存在计算效率低、误差大等缺点[4-5].为了提高PC斜拉桥施工控制精度和效率,秦顺全提出了一种基于无应力状态量控制施工过程结构内力和位移的方法,即无应力状态法[6-7].秦顺全基于最小势能原理推导了分阶段成形平面梁结构无应力状态法平衡方程,并进一步根据无应力状态量求得中间施工状态结构内力和位移[8];苑仁安等通过建立几何非线性杆系结构和平面梁单元无应力状态法平衡方程,探讨了分阶段成形平面杆或者平面梁结构最终状态内力和变形影响因素,否定了结构最终受力状态与结构形成过程有关的结论[9-10];孙志伟等推导了空间梁结构无应力状态法平衡方程,并通过算例验证了平衡方程的正确性和可靠性[11].但是上述文献对无应力状态法的研究并没有考虑混凝土收缩徐变效应对结构受力状态的影响.目前分阶段成形PC斜拉桥在确定合理施工状态时一般采用反复迭代的方式来考虑混凝土收缩徐变效应影响,然而对于施工阶段或斜拉索数量较多的结构(如大跨度预应力混凝土斜拉桥),反复迭代的计算方式必然会增大计算工作量,降低计算效率.因此通过探求混凝土收缩徐变效应对无应力状态量的影响规律,提出减少迭代次数的加速收敛方法对于无应力状态法理论的完善具有非常重要的意义.

1 无应力状态法加速迭代收敛研究

1.1 无应力状态法加速迭代公式推导

定义参数Δ及λ,在n>2的前提条件下,Δn为第n次正装成桥索力与目标成桥索力之间的差值,λn-(n+1)表示第n+1次正装成桥索力差值与第n次正装成桥索力差值的比值,即

(1)

从时刻t0到时刻t与应力σc(t0)相关的徐变效应总应变为

εc σ(t,t0)=σc(t0)φ(t,t0),

(2)

φ(t,t0)为混凝土徐变系数.

混凝土收缩常用收缩应变表示,收缩应变由自发收缩与干燥收缩两部分组成:

εc s(t,ts)=εc as(t)+εc ds(t,ts).

(3)

混凝土收缩徐变效应可用徐变效应总应变与收缩应变相加来表示,即

(4)

相同的施工阶段施工时间不变,混凝土收缩是与作用荷载无关而与时间有关,因此只有混凝土徐变对结构受力产生影响.因此有

Δεc=Δεc σ(t,t0).

(5)

随着斜拉索索力调整,结构受力及截面应力也将发生相应变化,有

(6)

进一步地,构件截面应力变化量引起的徐变系数变化比值为

(7)

φ0为名义徐变系数,各参数在本论文中为定值,则

(8)

进一步地,

式(9)表示无应力状态法第n+1次正装成桥索力差值与第n次正装成桥索力差值的比值与该次迭代混凝土收缩徐变效应的关系.

定义无应力索长修正系数β,在n>2的前提条件下,取

(10)

β随迭代次数的增加而改变,在第n次迭代计算过程中,βn的取值除了考虑本次迭代过程中混凝土收缩徐变效应的影响,同时也会受到前几次迭代过程中混凝土收缩徐变效应的影响,根据累加原理有

(11)

进一步地,第n+1次斜拉索无应力索长Sn +1为

Sn +1=Sn+βn(Sn-Sn -1).

(12)

上述推导主要基于混凝土徐变效应的变化比值与索力变化引起截面应力变化比值对应关系展开,式(12)即为考虑混凝土收缩徐变效应下的无应力状态法加速迭代收敛公式.

1.2 无应力状态法加速迭代计算流程改进

利用上文得到的无应力状态法加速迭代收敛公式对原无应力状态法计算流程进行改进,得到无应力状态法加速迭代计算流程(如图1所示).

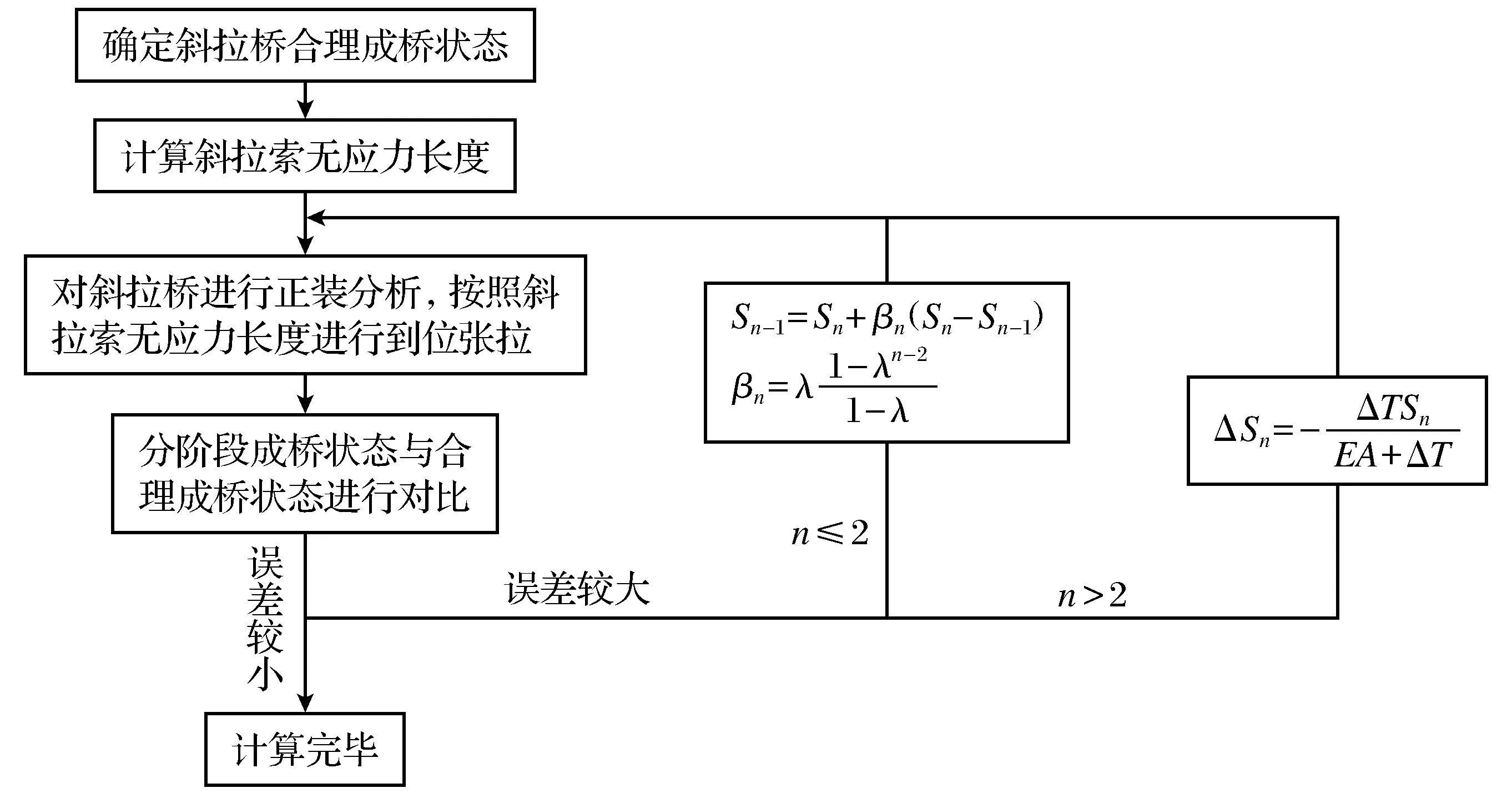
图1 无应力状态法加速迭代计算流程Fig.1 Accelerated iterative calculation process with unstressed state method

无应力状态法加速迭代计算流程在使用过程中的注意事项如下.

当正装成桥索力值与合理成桥状态目标索力值误差较大时,需要对无应力索长进行修正.并根据迭代次数n取不同的修正公式:

当迭代次数n≤2时,无应力索长依旧采用原公式[6-7],即

当迭代次数n>2时,无应力索长修正公式为

Sn +1=Sn+βn(Sn-Sn -1),

2 算例验证

为验证本文推导的无应力状态法加速迭代公式和迭代流程的可行性和适用性,以一座双塔PC斜拉桥为算例,在考虑混凝土收缩徐变效应前提下,分别按照原无应力状态法及本文提出的无应力状态加速迭代法来确定斜拉桥合理施工状态.

双塔PC斜拉桥平面布置图如图2所示.

人行斜拉桥基本参数见表1.

利用MIDAS/Civil 2015建立全桥空间有限元模型,如图3所示.辅助墩在模型中以支座的形式进行模拟,故在模型中不建立单元.

图2 斜拉桥平面布置图(单位:m)Fig.2 Layout plan of cable-stayed bridge(Unit: m) 表1 人行斜拉桥基本参数Table 1 The basic parameters of pedestrian cable-stayed bridge

构件材 料截面面积/m2惯性矩/m4截面高/m形心高/m主梁C50混凝土1.8430.9081.250.831主塔C40混凝土2.0980.4331.400.753拉索平行钢丝1.060×10-3———

图3 斜拉桥模型图Fig.3 Model graph of cable-stayed bridge

2.1 按原无应力状态法确定分阶段施工状态

在考虑混凝土收缩徐变效应对结构影响的前提下,按原无应力状态法对斜拉桥各施工状态进行五轮迭代计算后,成桥索力与目标索力相对误差控制在5%范围内,如表2所示.

由表2,以修正的斜拉索无应力长度作为到位张拉控制量重新进行第二轮正装模拟计算,分阶段成桥索力与目标索力相对误差最大值是10.69%,发生在LS1、RS1号斜拉索;对斜拉索无应力长度再次进行修正并进行正装计算,得到第三轮成桥索力与目标索力相对误差最大值发生在LS2、RS2号斜拉索为7.19%;按相同的迭代方法得到第四轮迭代计算后相对误差最大值是5.01%,发生在LM1、RM1号斜拉索;经五轮迭代后,索LS1、RS1分阶段成桥索力与目标索力最大误差值最大为2.89%,满足目标精度要求.综上,随着原无应力状态法迭代次数的增加,每轮迭代计算成桥索力与目标索力之间的相对误差值越来越小,可以理解为构件单元的无应力状态量越来越接近受混凝土收缩徐变效应影响后的单元无应力状态量,同时正装成桥状态越来越逼近混凝土收缩徐变效应影响下的合理成桥状态.

成桥目标状态及五次无应力状态法正装迭代计算得到的主梁竖向位移及弯矩分别如图4、图5所示.

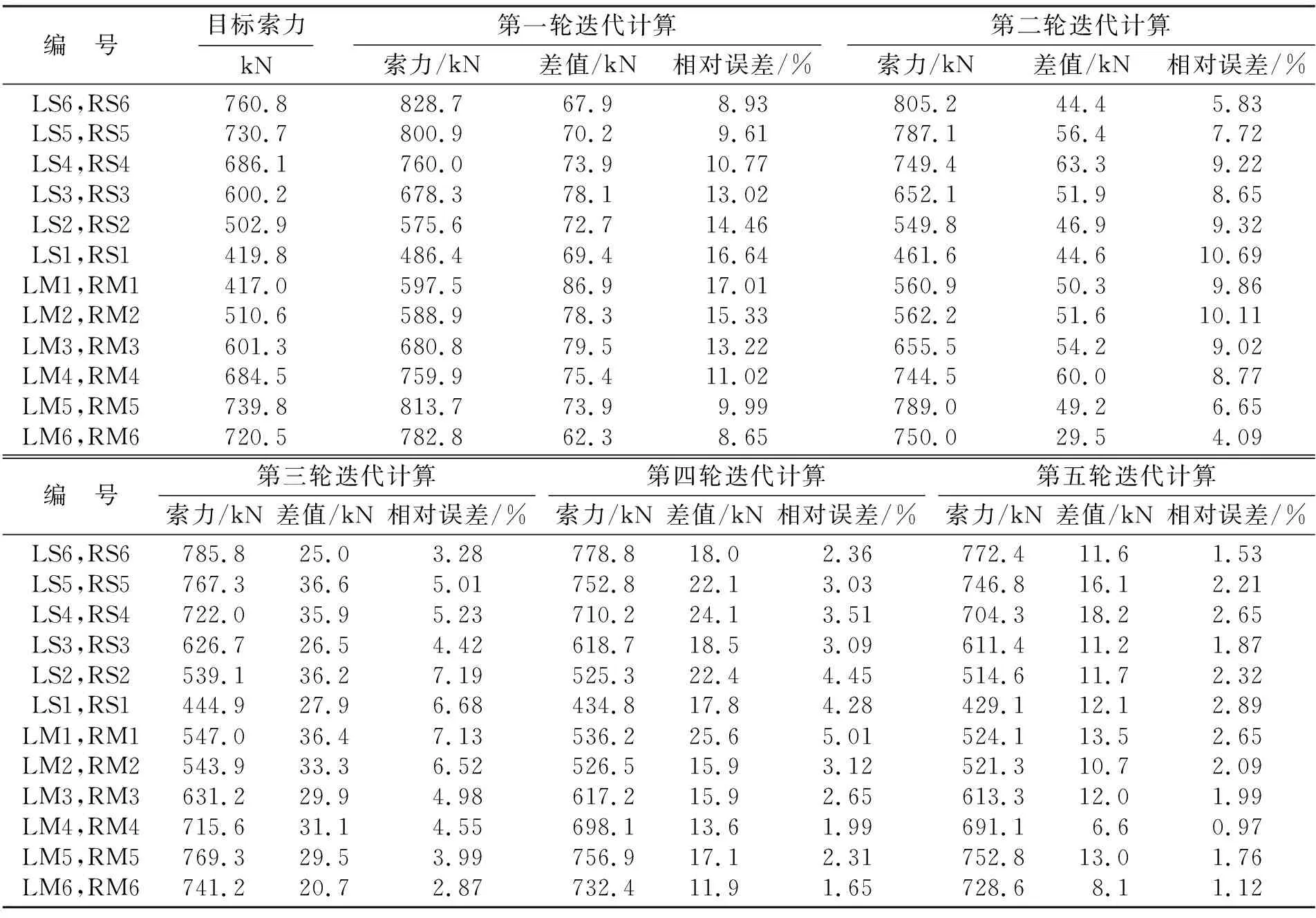
表2 无应力状态法迭代计算成桥索力与目标索力对比表Table 2 Comparative calculation of cable force and target cable force by iterative unstressed state method

图4 成桥目标状态及五次正装迭代主梁竖向位移图Fig.4 Target state of the bridge and vertical displacement of the main girder in the five positive loading iteration

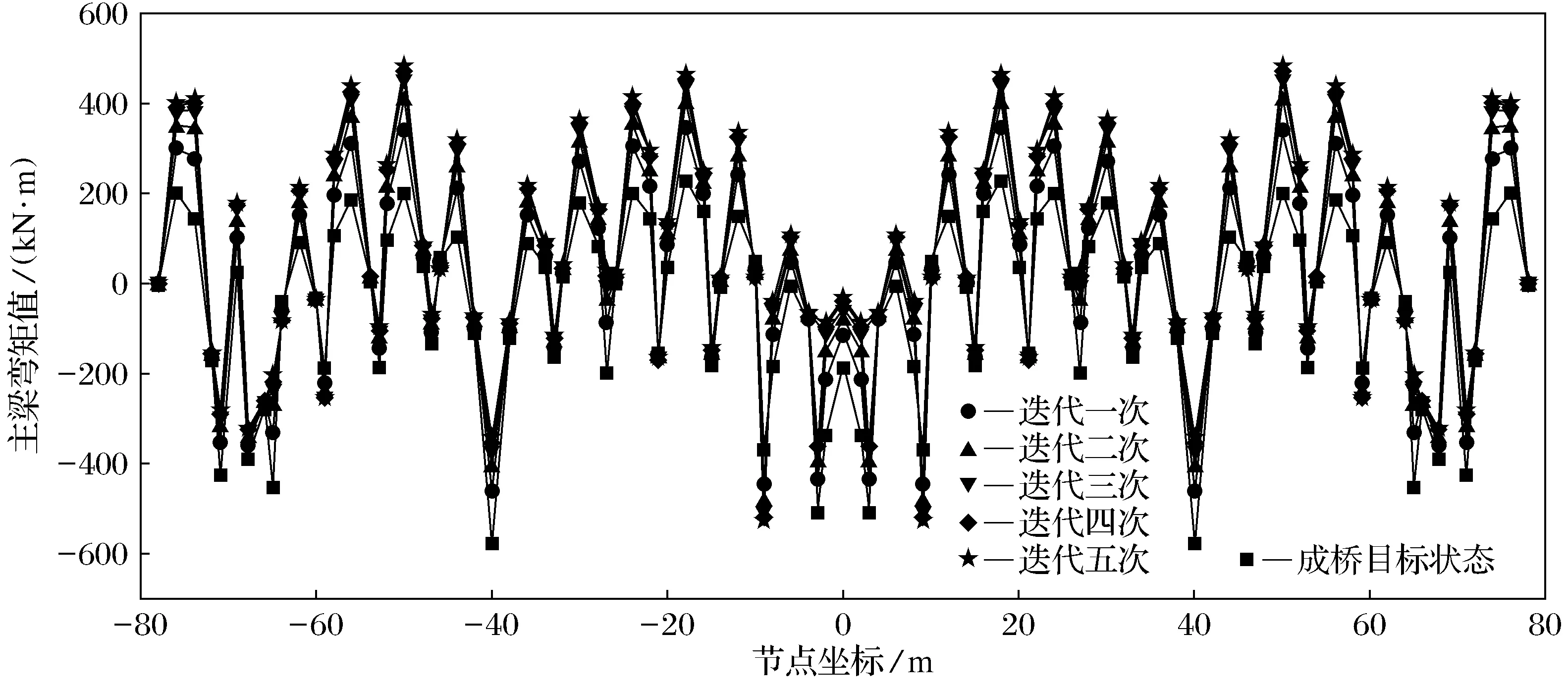
图5 成桥目标状态及五次正装迭代主梁弯矩图Fig.5 Target state of the bridge and the bending moment diagram of the main girder of the five positive loading iteration

由图4及图5所示,经过五轮正装迭代后,主梁竖向位移和弯矩均偏离了成桥目标状态下的结构受力和位移,并逐渐收敛于某一定值.按照无应力状态法基本原理,造成这种现象的主要原因是在保证各斜拉索索力值与成桥目标状态索力相一致的目标下,混凝土收缩徐变效应改变了塔梁及斜拉索单元无应力状态量,并进一步影响了主梁受力及竖向位移.

2.2 按无应力状态加速迭代法确定分阶段施工状态

按照无应力状态加速迭代法计算原则,当n≤2时,其计算步骤和方法与原无应力状态法相同;当加速迭代次数n>2时,按照本文推导出的无应力状态法加速迭代公式对斜拉桥进行加速迭代计算.

按照无应力状态法加速迭代计算流程计算得到第三轮迭代各斜拉索索力值,见表3.成桥目标状态及三次无应力状态法加速迭代计算得到的主梁竖向位移及弯矩分别如图6、图7所示.

对比表2和表3,按照原无应力状态法迭代五轮后其正装成桥索力与合理成桥索力值之间最大误差率为2.89%,发生在LS1及LM1号索;而

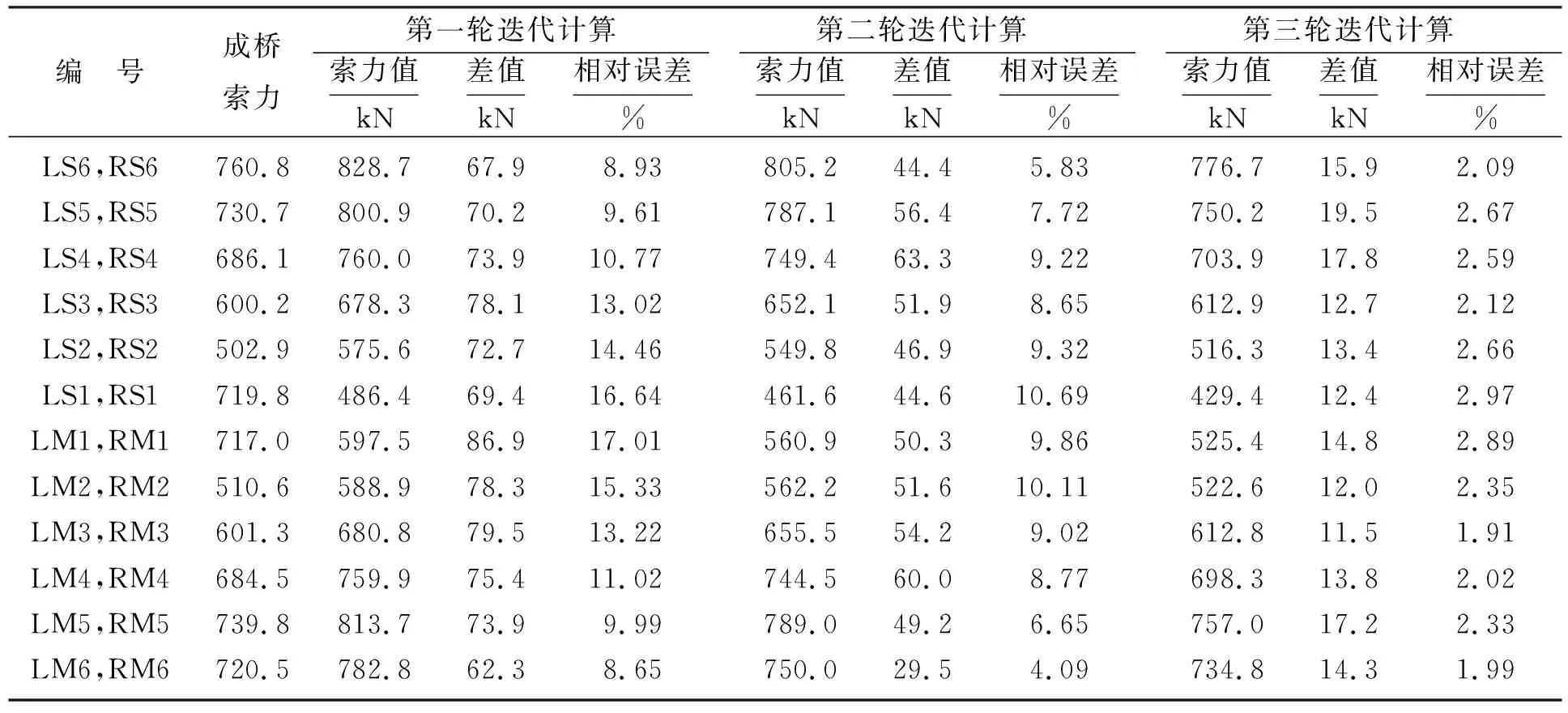
表3 无应力状态法加速迭代计算结果Table 3 Accelerated iterative calculation results with unstressed state method

图6 成桥目标状态及三次加速迭代主梁竖向位移图Fig.6 Target state of the bridge and vertical displacement of the main girder in the three accelerating iteration

采用无应力状态法加速迭代公式及加速迭代计算流程进行迭代计算,仅需迭代三轮即可达到较高的精度要求,成桥索力值与目标索力值之间最大误差率为2.97%,满足精度要求;分别对比图4、图5和图6、图7,无应力状态加速迭代法进行三轮正装迭代得到的主梁竖向位移、主梁弯矩与原无应力状态法进行五轮正装迭代得到的数值相吻合,同时计算工作量减少了将近一半.综上,本文提出的无应力状态法加速迭代公式及加速迭代计算流程减少了斜拉桥合理施工状态迭代计算次数和计算工作量,加快了计算速度,提高了计算精度.

图7 成桥目标状态及三次加速迭代主梁弯矩图Fig.7 Target state of the bridge and the bending moment diagram of the main girder of the three accelerating iteration

3 结 论

在考虑混凝土收缩徐变效应对分阶段成形PC斜拉桥影响的基础上,提出了无应力状态法加速迭代计算公式,改进了无应力状态法加速迭代计算流程,并以一座双塔混凝土斜拉桥为算例进行了验证.结论如下:

Sn +1=Sn+βn(Sn-Sn -1);

(2) 基于考虑混凝土收缩徐变效应的无应力状态加速迭代研究成果,改进了无应力状态法加速迭代计算流程,并对无应力状态法加速迭代计算流程中的注意事项进行了说明;

(3) 将加速迭代收敛公式和加速迭代计算流程在双塔PC斜拉桥算例中进行应用,数据结果表明研究成果能够减少依托工程的迭代次数及计算工作量,提高了计算效率及计算精度,具有很强的工程适用性和可行性.