基于CPSO的参数优化控制方法在SVC中的应用

赵熙临， 汤 倩， 吴胧胧， 徐光辉， 何晶晶

(湖北工业大学电气与电子工程学院， 湖北 武汉 430068)

0 引 言

随着社会经济的发展， 大量冲击性负荷接入电网， 导致不平衡负载的产生， 引起电网电压下降、 电压波动及功率因数降低等问题， 威胁电力系统的安全运行. 为解决该问题， 静止型无功补偿器(Static Var Compensator， SVC)被广泛应用于电力网络， 作为稳定电压及补偿无功的重要手段[1-4].

传统比例-积分(Proportional-Integral， PI)控制器以其结构简单、 容易实现、 被应用于无功补偿[5-6]. 由于传统PI控制器控制过程中参数固定， 无法根据系统状态进行自我调节， 导致控制性能难以达到更高要求. 在传统PI控制的基础上， 各种优化算法与其相结合的控制策略引起了众多学者关注. 文献[7]基于神经网络和粒子群优化算法， 设计出一种PI参数自整定的SVC控制方式， 用于实现SVC接入点电压稳定. 文献[8]利用蚁群算法对PI控制参数进行动态调节. 上述方法均提高了控制的鲁棒性， 但算法的复杂度以及计算量大， 不适用于在线控制. 粒子群优化(particle swarm optimization， PSO)算法是一种基于生物智能的随机迭代算法， 其特征是实现简单、 修改参数较少. 因此， 近年来PSO算法得到了研究者们的关注， 被广泛应用于电力系统无功优化、 最优潮流、 负荷分配等工程领域[9-13].

但综合分析针对PSO优化策略的研究不难发现， 该方法均普遍存在初始化盲目、 早熟而易陷入局部最优、 后期收敛速度过慢等问题. 为了提高粒子群算法的寻优精度， 众多学者对该算法做了不同的处理， 将混沌理论与其相结合便是其中之一. 文献[14]通过混沌序列选择全局最优粒子. 文献[15]在基本PSO算法基础上， 引入混沌理论， 根据早熟机制判断粒子是否采用混沌优化， 以此达到提高PSO算法寻优性能. 文献[16]将种群分为三部分， 通过粒子自适应值增减混沌粒子数目， 从而达到求解精度. 这些方法均在一定程度上提高了PSO的收敛精度.

本文提出一种新的混沌粒子群优化(Chaos Particle Swarm Optimization， CPSO)算法. 该算法通过混沌运动生成粒子群位置， 择优选取高质量粒子， 以加快收敛过程； 通过调整惯性权重增强其寻优能力， 防止发生交叉震荡； 同时对每一代全局最优值进行混沌映射， 以增加种群的多样性. 通过搭建电力系统无功补偿仿真， 验证了该方法的有效性.

1 粒子群优化算法及参数分析

1.1 PSO算法基本原理

粒子群优化算法利用rand()函数随机初始化种群， 经过N次迭代获取到全局最优解. 其本质是通过粒子间的信息传递及粒子对自身行为的修正， 不断改变其运动状态， 从而逐渐获得最优解.

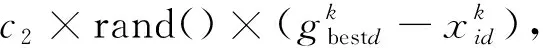
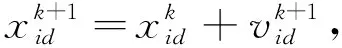
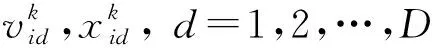
迭代过程中， 各粒子获取的目标函数值最小的位置记为Pbest=[pbest1,pbest2,…,pbestD]， 粒子群的目标函数值最小的位置记为Gbest=[gbest1,gbest2,…,gbestD].

1.2 惯性权重的影响分析

影响PSO算法寻优精度的重要参数之一是惯性权重w. 一般而言， 在一定的范围内，w值越大， 粒子的全局寻优能力越强； 反之， 算法的局部搜索更精确. 因此， 对于任一粒子而言， 当粒子位置远离Gbest时， 增大w值； 而当接近Gbest时， 减小w值的搜索方式更符合实际优化需求.

考虑到基本PSO寻优的非线性特征， 采用线性递减的策略将不能满足实际需求. 因此， 本文采用一种基于粒子个体适应值的自适应调节策略， 即每个粒子的w依据其当前适应值来进行调整， 调整规律满足

(3)

式中：ωmin,ωmax分别为惯性权重w设定的下限和上限；fav为粒子群目标函数值的当前平均值；fmin为当前Gbest的目标函数值；fi为粒子当前的适应值. 一般来说， 惯性权值ωmin=0.4，ωmax=0.9时算法的性能最好[17].

（2）模拟结果与分析 首次浇高设定为冒口的3/5高度，冷却2h后进行补浇操作，让温度1590℃的同种钢液从冒口顶部注入冒口内，浇满后再次进入冷却凝固阶段。补浇时型腔内温度场如图2所示，从图中可以看到，补浇初始时铸件的凝固率并不高，约为18%，补浇的高温钢液与型腔内原有钢液立即均匀混合，随着补浇的进行，凝固率逐渐降低。最终缩孔判据（Shrinkage Porosity）预测的缩孔位置与未进行补浇的情况是一致的，即没有实现通过补浇增加冒口模数和减弱冒口下偏析的目的。

2 基于混沌映射的粒子群优化算法

混沌优化的关键在于如何将待控变量通过混沌映射进行处理. 将混沌理论融入PSO算法， 具体为： ① 通过混沌运动生成各粒子的位置， 从中选出所需种群， 以此保证粒子分布的均匀性， 同时提高粒子的质量； ②Gbest通过混沌映射产生混沌序列， 并将混沌序列随机代替原种群中的部分粒子， 以此提高种群多样性. PWLCM混沌映射方式如下：

(4)

式中：Zn表示混沌变量. PWLCM混沌具有随机性的运动状态， 如其它混沌系统一样， 其遍历特性使得混沌变量在一定范围内按照自身“规律”不重复遍历整个解空间， 图 1 为PWLCM混沌映射对单个Z0迭代500次得到的混沌向量， 很好地体现了其遍历性.

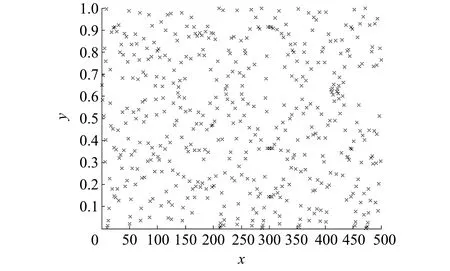
图 1 PWLCM混沌映射的遍历性Fig.1 The ergodicity of PWLCM chaotic maps

CPSO算法流程如下：

步骤 1 初始化粒子群基本参数， 包括学习因子、 惯性权重取值范围、 种群规模、 粒子维数、 最大迭代次数、 最小目标函数值以及速度和位置的取值范围.

步骤 2 混沌初始化

1) 利用随机函数产生一个D维且各分量值均在[0,1]之间的混沌矢量Z1=(Z11,Z12,…,Z1D)， 以Z1为初始值通过映射式(4)， 计算获取M(M>N)个矢量Z1,Z2,…,ZM.

2) 将混沌矢量Zi(i=1,2,…,M)的各分量按式(5)线性变换到解空间， 得到M个矢量x1,x2,…,xM.

xij=aj+(bj-aj)zij,

i=1,2,…,M;j=1,2,…,D,(5)

式中：bj,aj为优化变量上下限.

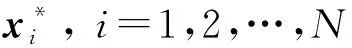
步骤 3 将个体的历史最优位置设为个体最优Pbest， 群体中历史最优位置设为全局最优Gbest.

步骤 4 判断是否满足循环条件， 若循环结束， 则输出全局最优位置Gbest； 否则， 各粒子按照式(1), 式(2)更新自身信息.

步骤 5 计算更新后各粒子目标函数值， 记为fitness， 若该粒子fitness的比其Pbest的fitness更小， 则将此位置设为Pbest； 若该粒子的fitness比Gbest的fitness更小， 则将此位置设为Gbest.

步骤 6 全局最优位置混沌化

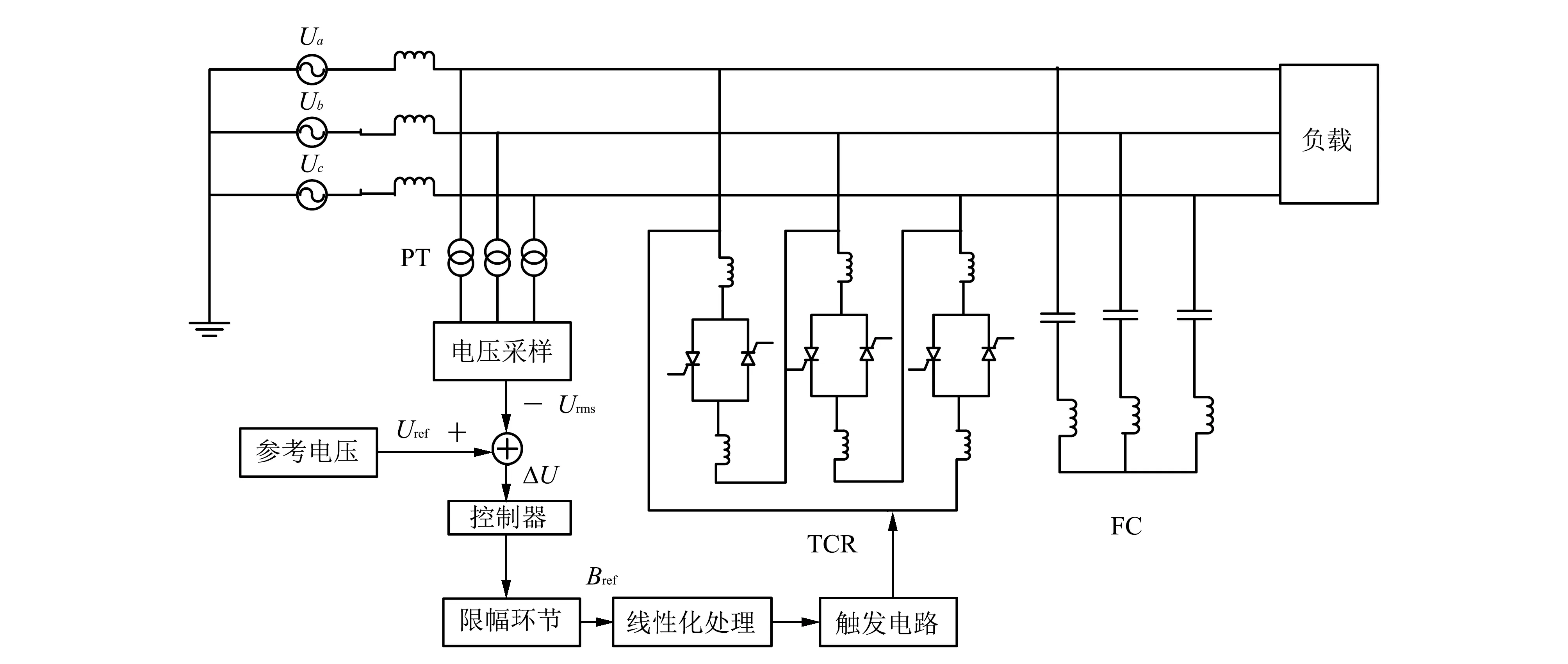
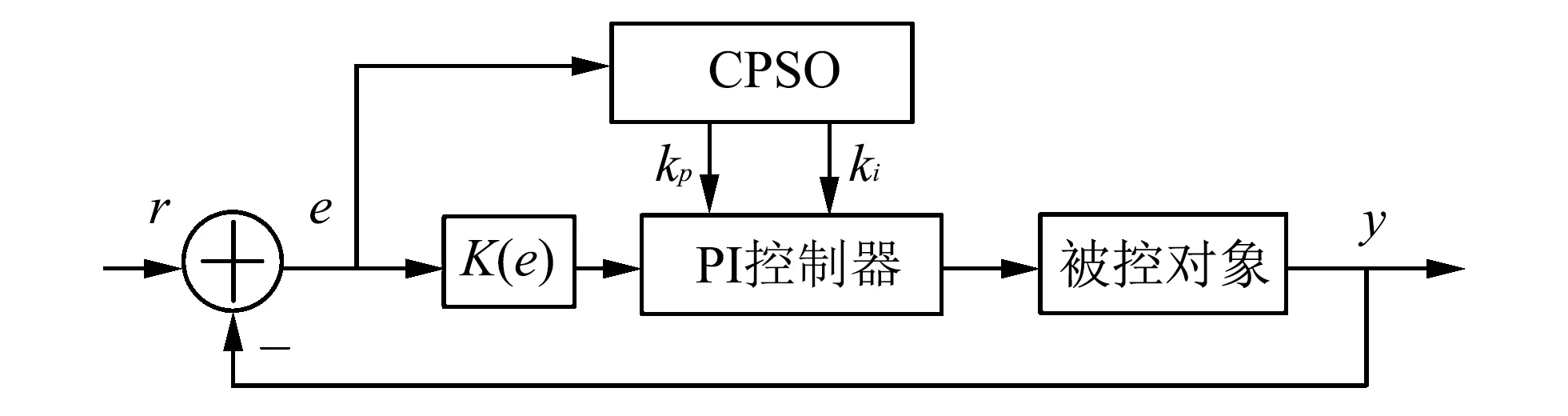
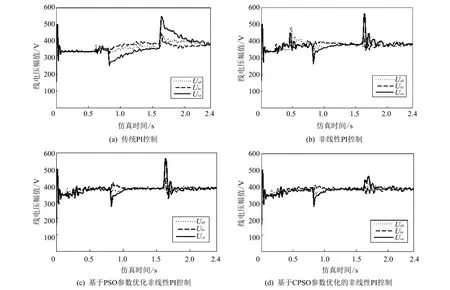
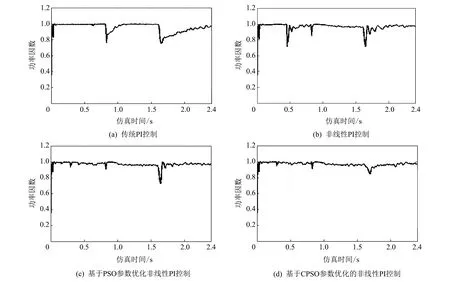
1) 对每一代全局最优位置xg=(xi1,xi2,…,xiD)混沌优化.xg通过式(6)转换得到Z1j=(Z11,Z12,…,Z1D),j=1,2,…,D， 并对Z1j各分量通过映射式(4)进行L-1(L

(6)

2) 混沌矢量Z通过式(5)变换到待优化问题的可行空间， 生成可行解序列x=(x1,x2,…,xL).

3) 从种群中挑选L个粒子， 要求各粒子不相同且不是当前Gbest， 用可行解序列替换被选中粒子， 并计算可行解序列的fitness， 若小于当前Gbest的fitness， 则更新Gbest.

步骤 7 判断是否满足结束条件(当前迭代次数大于最大迭代次数或者Gbest的目标函数值小于最小目标函数值)， 若不满足条件则跳至步骤4； 若满足则输出Gbest， 并结束程序.

3 基于CPSO的SVC控制方法

SVC应用于负载补偿时， 其作用是稳定负载电压， 补偿负载无功， 一个典型的SVC系统框图如图 2 所示.

图 2 中：Urms为SVC安装点处线电压，Uref为系统参考线电压设定值. 误差信号ΔU=Uref-Urms用于计算补偿电纳Bref. 触发电路环节根据触发角信号产生触发脉冲送至主电路， 主电路的电压随之发生改变， 改变后的电压再通过反馈环节送至控制器计算， 直到SVC接入点电压与参考电压达到一致为止， 以保持期望的功率因数.

图 2 SVC系统结构图Fig.2 Architecture diagram of SVC system

基于CPSO的SVC控制系统框图如图 3 所示， CPSO优化对象为PI控制器参数kp,ki. 为提高系统初期响应的快速性， 在此控制器采用基于非线性函数k(e)的PI控制器. 其非线性增益函数表现为

k(e)=1+4.5[1-sech(0.05e)],(7)

式中：e为给定值与实际值的误差.

图 3 基于CPSO的SVC控制系统框图Fig.3 Block diagram of SVC control system based on CPSO

4 系统验证

为验证本文所提混沌粒子群优化算法， 利用matlab建立SVC系统仿真模型. 采用ITAE准则， 作为目标函数， 其函数形式为

式中：t表示仿真模型运行时间.

将待控系统负载状态分为三段： 第一段为平衡负载； 第二段为突加不平衡负载； 第三段为不平衡负载剔除. 目的在于验证系统负载突变情况下的无功补偿能力. 为达到更优的控制效果， 考虑到不平衡负载的特征， 拟将负载的不平衡负序电流基波分量作为切换信号， 当负载状态突变时， 系统自动选择不同参数的PI控制模块.

仿真验证过程中， 系统采用相电压为220 V， 设置线路寄生电抗为LS=0.649 mH. 平衡负载由三相RLC负载代替， 其参数设置为100 kW有功和86 kvar感性无功. 设定在0.8 s时突加缺失B相的负载， 其中有功50 kW， 感性无功70 kvar； 在1.6 s时将不平衡负载剔除. 传统PI控制器参数以及非线性PI控制器参数选择均为kp=0.000 55，ki=0.002. 为了比较优化效果， 采用基本PSO和本文所提CPSO算法求解该优化问题， 迭代过程中所用的目标函数、 SVC仿真模型、 初始化参数设置均一致， 其参数优化结果如表 1 所示.

表 1 基于PSO和CPSO的优化参数结果

针对三相线路电压的稳定性和系统功率因数的提高， 不同控制方式的控制结果如图 4， 图 5 所示.

图 4 三相线电压响应曲线图Fig.4 Three-phase voltage response curve

图 5 系统功率因数图Fig.5 System power factor diagram

由图 4， 图 5 及表 2 可以得出， 当第二段突加不平衡负载和第三段不平衡负载剔除后， 在CPSO参数优化的非线性PI控制作用下， 三相线电压在负荷过程中， 冲击电压明显减小， 功率因数提高显著， 且在允许范围内， 相比其他控制方式具有更好的性能.

表 2 控制效果比较

5 结 论

针对传统PSO算法存在早熟导致陷入局部最优解以及后期收敛速度过慢的问题， 提出了一种基于混沌理论的自适应粒子群优化算法. 该算法通过混沌初始化， 以加快收敛进程； 其次， 粒子根据自身状态调整惯性权重以增强搜索能力； 同时， 对每一代全局最优解进行混沌映射， 以增加种群的多样性. 基于该优化算法的电力网络无功补偿控制的仿真， 验证了该算法的有效性.