班轮联盟调箱优化模型及激励机制设计

刘荣亮，史立，冯杰

(上海海事大学物流科学与工程研究院，上海 201306)

0 引 言

在全球经济一体化进程持续推进的今天，高效且便于管理的集装箱运输取得了长足发展，并一跃成为近几十年来发展最快的运输方式之一，相信在今后的跨国贸易运输中，集装箱运输势必会凭借其特有的优势占据主导地位。然而，国际贸易的失衡往往导致各地区的进出口货运量之间存在显著差异，使得大部分空箱积压在进口区域，而出口区域却恰恰相反。为满足货物运输需求，调运空箱便无法规避，然而调箱本身并不会为班轮公司创造任何经济效益，相反班轮公司还会因调度工作的开展而产生较高的运输费用。因此，如何高效合理地进行调箱对班轮公司降低运营成本、提高运营效益至关重要。

集装箱调箱是一个涉及多方面的复杂问题，不仅要全面分析不同时刻、不同节点的空箱实际需求量和供给量，还需要综合考虑航次、航线等各相关要素。一方面，若班轮公司的多余空箱未能及时调运，则不仅会使空箱资源得不到充分利用，还会产生不菲的空箱堆存费用；另一方面，若班轮公司空箱需求未能得到及时满足，就不得不从租箱公司高价租箱以满足客户的运输需求。目前，应用比较普遍的调箱方法大多是在班轮公司独立运营的基础上提出的，极少考虑到班轮公司间的合作关系，这是因为各班轮公司的最终目标是追求各自利益最大化，在与其他公司合作中，各公司最优决策的不一致甚至冲突将使合作持续性受到严重影响。

本文的目标是通过分析调箱和班轮联盟，对基于空箱互租和舱位互租结成的联盟进行定量分析，在联盟成员间进行空箱互租和舱位互租，并设计激励机制，从而使班轮联盟更高效合理地调度其内部空箱，实现联盟和各成员利益的最大化。目前针对调箱的研究成果主要分为两大类。一种是定性地设计一套处理空箱问题的经验方法，比如：徐剑华[1]对集装箱的运输情况和问题成因展开了全面细致的定性研究，并给出了相应的经验措施，包括鼓励班轮公司之间进行战略联盟以实现共用空箱，班轮公司与租箱公司之间达成合作关系使班轮公司能根据自己的实际情况选择租还箱地点等。另一种以调箱为切入点建立合理的数学模型使调箱成本最小，比如：SHEN等[2]针对是否租用或归还空箱建立了调箱优化模型，同时设计了相应的决策支持系统以解决班轮公司调箱问题；施欣[3]在综合考虑重箱与空箱运输的基础上建立了海运集装箱调箱优化模型，并通过GAMS软件对该模型进行模拟；DANG等[4]针对一个港口区域中多个场站的调箱问题，考虑单位时间内场站空箱需求，建立了基于综合调箱和租箱策略的调箱模型；FRANCESCO等[5]为解决在不确定港口影响下的海运调箱优化问题建立了多方案规划模型；SHU等[6]考虑了重箱、空箱、租借箱等不同情况下的调运，且每种集装箱调运的费用不同，结合班轮公司的船期表构建一个时间扩展网络流图，并用优化软件对模型进行求解，从而得出在成本最小情况下的最优重箱和调箱方案。在班轮联盟调箱研究方面：杨洋[7-9]以班轮公司间合作共享调运资源为基础，在保证所有参与调箱合作的班轮公司的需求都得到满足的条件下，建立了一个以空箱获取综合成本最小为目标的海运调箱模型；陈继红[10]对班轮联盟各流程协同机制和管理模式展开了深入分析，得出决定班轮联盟协同发展的因素为这些机制作用总和的结论；邢玉伟等[11]建立了基于空箱互租战略的班轮航线各不同航段的动态调运优化模型，并设计了一种与时间相关的动态算法以实现决策期内调箱总成本最小。

然而，以上文献大多立足于单家班轮公司或聚焦在联盟如何合作来降低调箱成本上，很少考虑公司间能不能成立联盟以及如何维持联盟的稳定性等问题。在此方面也有相关研究：一种是从非合作博弈的角度对双方策略展开研究，比如ZHOU等[12]以非合作博弈理论为基础，对在两港口开展业务的双寡头班轮公司的服务定价策略展开了深入分析；另一种是以合作博弈为理论工具对基于运力互租形成的战略联盟的收益分配机制展开研究，比如SONG等[13]认为基于合作博弈理论模拟联盟内部的组织行为是可行的，但仅列举了2个简单案例说明利益分配问题。李建忠等[14]表示若双寡头班轮公司共享集装箱，则不仅能使集装箱资源得到充分利用，还能够减少不必要的调箱，有利于双方获得更多的经济收益，实现双赢。

在此假定几个班轮公司组成战略联盟。考虑到各成员在实际运营中是相互独立的，各自的决策都是努力使自己的收益最大。在这种情况下，各成员的最优决策往往与联盟的最优决策产生冲突，若一味地要求内部成员按照联盟的最优决策运营，则联盟必将面临解散的风险。本文在以上文献研究的基础上，从班轮联盟角度出发，以联盟收益最大为目标，对班轮公司之间通过空箱互租和舱位互租解决调箱问题的模型和方法进行研究，并设计激励机制使得班轮联盟与各成员的最优决策一致，实现双赢。

1 班轮联盟调箱问题描述

班轮公司在独自运营的情况下能力有限，加之部分航线周期长，极易出现部分港口空箱大量积压而其他港口空箱却严重短缺的问题，为及时满足客户运输需求，班轮公司不得不选择从租箱公司高价租箱，这不仅使得自家空箱使用率降低，还会造成自身的营运成本大大增加。此外，在实际运营中，班轮在某些航段会出现舱位空置的情况，部分舱位未得到有效利用，造成资源的浪费。为提高班轮公司资源利用率，降低运营成本，班轮公司之间以空箱互租和舱位互租为基础结成战略联盟。为维持联盟的稳定性，需要设计一种机制使得各成员与联盟的最优决策一致，实现双赢。

首先，假设联盟内部所开展的空箱互租和舱位互租为有偿业务。以出租空箱和舱位的方式为班轮公司提供补偿性支付被称为旁支付(side payment)。这样，班轮联盟成员的收益包括3部分：一是依靠承运货物获得的收益；二是利用出租或租用空箱获得的旁支付；三是利用出租或租用舱位获得的旁支付。为使各成员与联盟的最优决策保持一致，本文在班轮联盟调箱模型优化的基础上设计合理的旁支付，对班轮联盟及其成员的决策分别建立整数规划模型，并通过逆优化技术使各成员与联盟的最优解一致。

2 联盟集中决策模型

参数：A为班轮联盟内班轮公司的集合，a,k∈A；P为港口集合，i,j∈P；Raij为a公司从港口i到j承运单位集装箱货物的收益；Caij为a公司从港口i到j单独承运自家空箱的单位成本；Xaij为a公司从港口i到j承运货物的箱量；Yaij为a公司从港口i到j单独承运自家空箱的箱量；Hai为a公司在港口i原有的空箱存量；Hait为a公司在港口i经过时间t运完货物后的空箱存量；Ci为单位空箱在港口i的堆存成本；Uaij为a公司从港口i到j的运力限制；Mi为港口i最大空箱存储量；Yakij为a公司租用k公司的舱位运输从港口i到j的自家空箱量；Dai为a公司在港口i的空箱需求量；Yaki为a公司在港口i租用k公司的空箱数量；p为联盟内空箱互租价格；r为联盟内舱位互租价格；La为公司a承运货物获得的收益；Wa为公司a出租或租用空箱获得的旁支付；Qa为公司a出租或租用舱位获得的旁支付；Sa为公司a加入联盟后获取的总收益，有Sa=La+Wa+Qa。

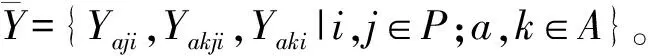
若班轮公司在承运重箱时有空余舱位，则承运空箱的附加成本很小，在这里就不考虑该成本，因此联盟集中决策模型为

(1)

s.t.

(2)

Hki+Dki≥Xkij

(3)

(4)

Xkij+Yakij≤Ukij

(5)

Xkij-Yaki=Hkit

(6)

(7)

Xkij,Ykji,Ykai,Ykaji,Hki,Hkit≥0

(i,j∈P,i≠j;a,k∈A,a≠k)

(8)

式(1)为目标函数，其中第1部分指联盟承运货物而获取的全部收益，第2部分指因调运空箱而产生的成本，第3部分指集装箱的堆存费用；式(2)表示联盟原有空箱堆存量不能超过港口堆存限制；式(3)确定班轮公司的空箱需求，即班轮公司在港口的空箱存量与空箱需求量之和应满足调运重箱所需要的箱量；式(4)表示班轮公司自己调箱量、租箱量和通过租用其他班轮公司的舱位调运的空箱量之和应满足空箱需求；式(5)表示班轮公司运输重箱和租给其他班轮公司舱位运输空箱的总量不能超过其运力限制；式(6)表示港口现有空箱存量，即原有空箱量+自己调箱量+租箱量+租用其他班轮公司舱位调运的空箱量-运出重箱量-租给其他班轮公司的空箱量=港口现有空箱存量；式(7)表示港口现有空箱存量不能超过其堆存限制；式(8)表示决策变量为正数。

3 基于空箱和舱位互租价格的机制设计

为设计一个合理的机制促使成员与联盟的最优决策达成一致，假设在联盟中成员k发挥着主导作用，其目标在于获取更多的经济效益。对成员k的决策建立数学模型。

班轮公司k加入联盟的决策模型(也称为联盟成员k决策模型，记为CPk)为

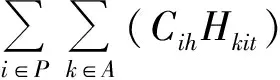
(9)

s.t.式(2)～(8)。

式(9)中，在等号右侧：第1部分指班轮公司k承运货物获取的收益；第2部分指班轮公司k对外出租空箱收取的费用；第3部分指班轮公司k租用联盟其他成员的空箱支付的费用；第4部分指班轮公司k对外出租舱位收取的费用；第5部分指班轮公司k租用联盟其他成员舱位支付的费用；第6部分指班轮公司k独自进行调箱的费用；第7部分指集装箱在港口的堆存费用。

班轮公司k不加入联盟的独立决策模型为

(10)

s.t.式(2)、式(3)、式(7)，以及

(11)

Xkij≤Ukij

(12)

(13)

Xkij,Ykji,Ykij,Hki,Hkit≥0，

i,j∈P；i≠j

(14)

相较于目标函数式(9)，式(10)中班轮公司k的收益仅来源于承运货物；式(11)与式(4)相比，班轮公司空箱需求只能通过自己调运获得；式(12)与式(5)相比，班轮公司只承运自己的重箱；式(13)与式(6)相比，班轮公司没有了出租或租用空箱以及通过出租或租用舱位进行调箱等活动；式(14)表示决策变量为正数。

用yb、ylb、ylfdb、ylfbd、yfldb、yd分别表示CPk的约束条件(2)～(7)的对偶变量。CPk的对偶问题为

min (Miyb+Dkiylb+Ukijylfbd+Hkityfldb+Miyd)

(15)

s.t.

ylb+ylfbd-yfldb≥Rkij

(16)

-yflbd≥p

(17)

ylfdb+yfldb≥-p

(18)

ylfdb+yfldb≥r

(19)

ylfdb+yfldb≥-r

(20)

ylfdb≥-Ckji

(21)

yb-yd≥Ci

(22)

yb,ylb,ylfbd,yd≥0；ylfdb≤0；yfldb无约束

(23)

该对偶问题的互补松弛性约束条件为

若Xkij>0则ylb+ylfbd-yfldb=Rkij

(24)

若Yaki>0则-yflbd=p

(25)

若Ykai>0则ylfdb+yfldb=-p

(26)

若Yakij>0则ylfdb+yfldb=r

(27)

若Ykaji>0则ylfdb+yfldb=-r

(28)

若Ykji>0则ylfdb=-Ckji

(29)

若Hkit>0则yb-yd=Ci

(30)

若式(2)不成立则yb=0

(31)

若式(3)不成立则ylb=0

(32)

若式(4)不成立则ylfdb=0

(33)

若式(5)不成立则ylfbd=0

(34)

若式(6)不成立则yfldb=0

(35)

若式(7)不成立则yd=0

(36)

定理1INVP总存在可行解。

证明具体过程参考文献[16]。

定理1说明总是可以找出合适的p和r，使成员与联盟的最优解保持一致。在通常情况下，p和r的取值是一个范围，因此可不考虑航线对p和r的影响。若取INVP的某一可行解p和r，那么成员k获取的全部收益为Sk=Lk+Wk+Qk，其中

在INVP中增加下面的理性约束条件是必要的，即联盟能够合作成功应同时满足下面2个条件：

(37)

(38)

式(37)指联盟所获得的收益均分配给了每个成员；式(38)指班轮公司加入联盟后所获得的收益应高于独立运营时的收益。

4 实 例

4.1 已知条件

假设有2家班轮公司a和k在4个港口之间进行班轮联盟调箱，且这2家公司的航线相同，均在4个港口间相互运输。班期为一班轮公司到达港口i(i=1,2,3,4)后，另一班轮公司从该港口出发。如果班轮公司缺箱，则只能租用另一班轮公司舱位进行调箱或者独自承运空箱，若是等待到该港口的自家船舶调运来的空箱将会延误班期。班轮运输上限为2 000 TEU，且都为标准箱，不考虑外界租箱情况。某时刻，班轮公司a和k在各港口的空箱拥有量(Hai、Hki)和单位空箱堆存成本(Ci)见表1，班轮公司a和k在港口间重箱运输量(Xaij、Xkij)、单位重箱运输收益(Raij、Rkij)、单独调运自家空箱的单位成本(Caij、Ckij)分别见表2～4。

表1 班轮公司a和k在港口的空箱拥有量Hai、Hki和单位空箱堆存成本Ci

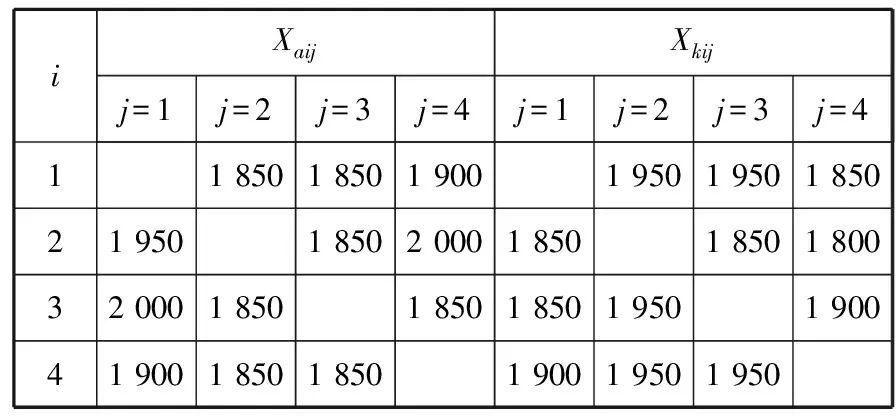
表2 班轮公司a和k在各港口间的重箱运输量Xaij、Xkij TEU

表3 班轮公司a和k在各港口间单位重箱运输收益Raij、Rkij 美元/TEU

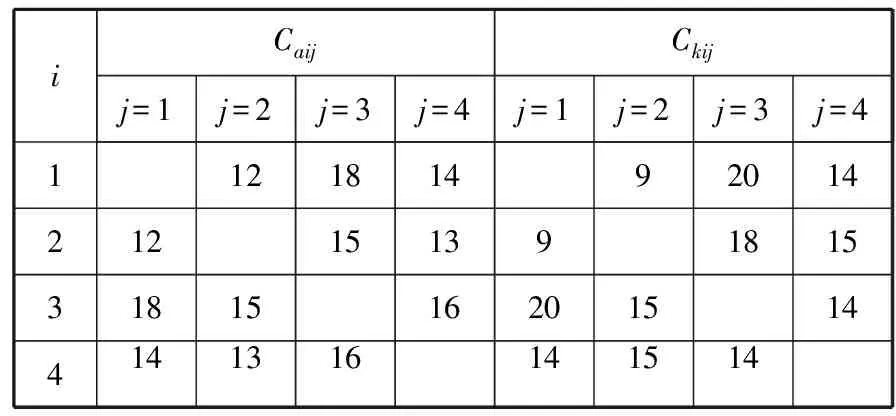
表4 班轮公司a和k在各港口间单独调运自家空箱的单位成本Caij、Ckij 美元/TEU

4.2 算例结果及其分析

利用Lingo 11先对联盟集中决策模型进行求解，在空箱互租和舱位互租的情况下，得到目标函数即联盟总收益为6 736 700美元，班轮公司a和k在各港口互租箱量和互租舱位调运的自家空箱量见表5和6。

表5 班轮公司a和k在各港口互租箱量Yaki、Ykai

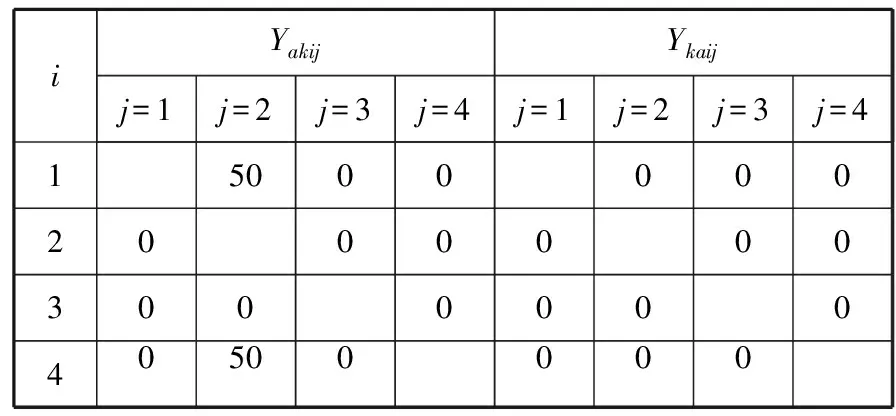
表6 班轮公司a和k互租舱位调运的自家空箱量Yakij、Ykaij TEU

再对班轮公司不加入联盟的独立决策模型进行求解后可知，在班轮公司独自运营的情况下，其收益总额为6 705 000美元，班轮公司a和k单独调运的空箱量见表7。

将以上数据代入INVP利用Lingo求得空箱互租价格p∈[0,10美元]，舱位互租价格r∈[0,9美元]，p和r对各成员收益的影响见表8。

表7 班轮公司a和k单独调运的空箱量Yaij、Ykij TEU

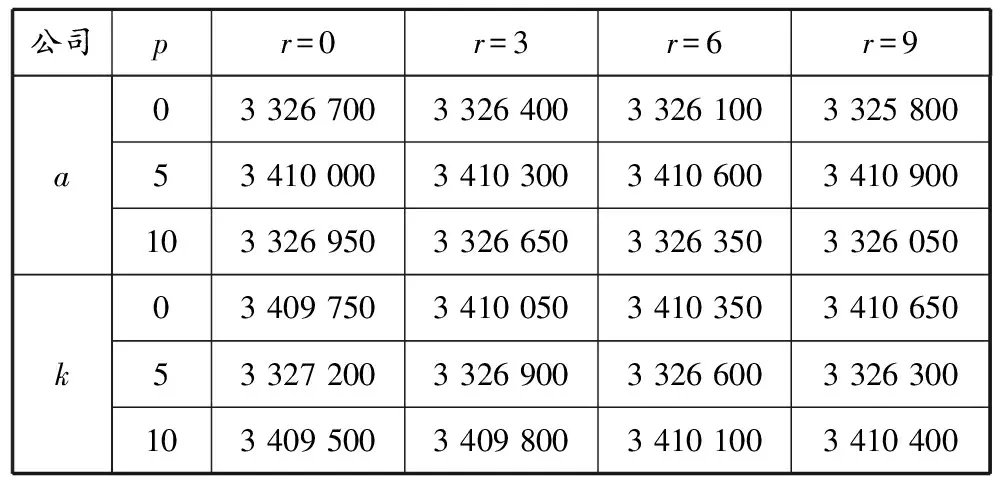
表8 加入联盟后p和r对班轮公司a和k收益的影响 美元

分析表5～8可知，在航线和调运条件一致的情况下，采用同样的优化调运理念，班轮公司a和k调运空箱的结果在联盟前后发生了明显变化。

(1)以空箱互租和舱位互租为基础而形成的合作调运，能够增加所有加入联盟的班轮公司的收益。如该算例所示：在班轮公司联盟的情况下，联盟总收益为6 736 700美元；在班轮公司独自运营的情况下，班轮公司a和k公司各自的收益分别为3 309 700美元和3 395 300美元，总和则为6 705 000美元。在合作调运过程中，联盟成员可将其暂时处于闲置状态的集装箱出租给联盟其他成员，这样不仅班轮公司能够获得一定的租箱费用，同时降低空箱堆存成本，而且可以减少其他班轮公司的调箱成本。在重箱运输中，班轮公司可将自己多余的舱位租借给联盟中其他班轮公司用以调运空箱，这样既能减少闲置资源的浪费，又能通过舱位出租收取一定的费用，还能避免其他班轮公司单独进行调箱，最终实现互利共赢。

(2)从长远看，班轮公司在结成联盟的情况下空箱使用率更高，并可最大限度地避免调箱从而获取更大的经济效益。然而，尽管在p和r各自合适的价格区间内，所有p和r均可令内部成员根据联盟的最优决策进行运作，其合作收益都高于独立运营时的收益，但是不同的p和r会带给成员不同的收益(如图1所示：在p越高、r越低的情况下，班轮公司a越受益；相反，在p越低、r越高的情况下，班轮公司k越受益)。至于如何选取具体的p和r，笔者认为这是联盟成员之间根据自身实际情况讨价还价的结果。

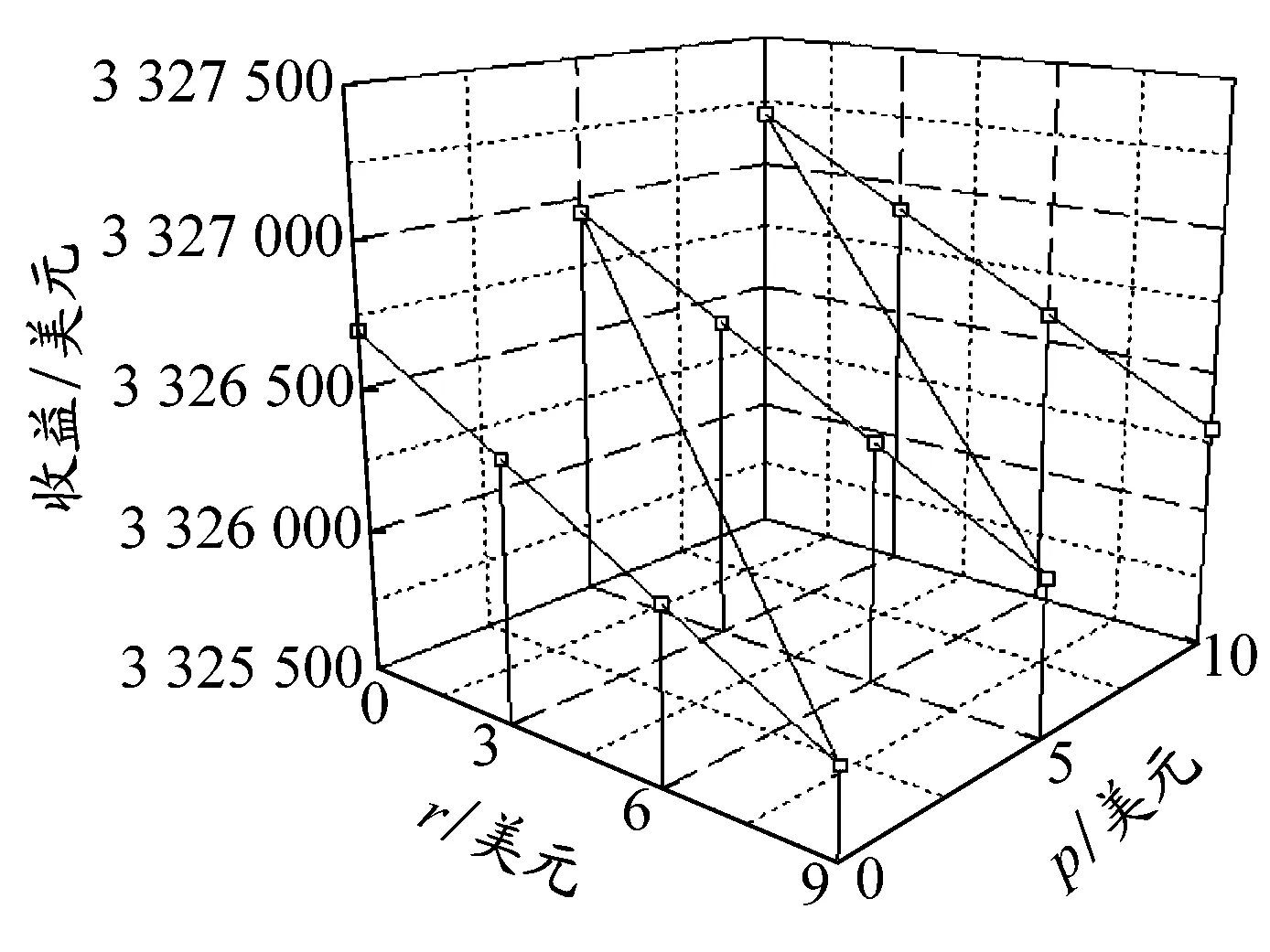
a)班轮公司a收益情况

b)班轮公司k收益情况

5 结束语

如今集装箱在国际贸易运输中扮演的角色越来越重要，如何提高空箱利用率，降低调箱成本成为当前一个热门的研究课题。与以往的研究不同，本文针对港口空箱需求特征，研究了班轮联盟空箱互租和舱位互租战略下的调箱问题，构建了班轮联盟收益最大化的整数规划模型和求解算法。运用算例加以验证，得到了基于空箱互租和舱位互租进行调箱的最优决策，弥补了现有联盟调箱研究的不足。通过设计激励机制，促使联盟内部积极进行空箱互租和舱位互租活动，在充分利用空箱的基础上降低调箱成本。本文激励机制设计的核心是以逆优化技术确定空箱互租价格和舱位互租价格，以此促使成员根据联盟最优决策进行运作，在实现各成员收益最大化的同时也使得联盟收益最大化，实现双赢，进而保障合作的稳定性。

由于没有对模型进行仿真分析，本文无法进一步论证该优化模型的稳定性，文中算例只能说明模型的可行性却无法证实模型在实际运作中的普遍适用性，所以未来的研究应对模型进行更深入细致的论证。同时，本文研究的是一个静态决策过程，而在实际运营中，需求、班期和港口空箱数量等均会随时间变化。在这种动态情况下，如何合理地决策以及如何确定合适的空箱互租价格和舱位互租价格值得进一步研究。