基于稳流电路退化过程建模的激光惯组剩余寿命预测方法
2019-01-07刘晶晶黄丽莎
刘晶晶 黄丽莎
1.宇航智能控制技术国家级重点实验室,北京 100854 2.北京航天自动控制研究所, 北京 100854 3.北京航空航天大学,北京 100191
惯组是飞行器上的关键部件,它的正常工作与否直接关系到飞行器是否能按照预定路线准确运动。随着惯组性能的不断提高及系统复杂性的不断增加,惯组的可靠性、维修性等问题日渐突出。
惯组故障主要由电路元件故障和惯性器件故障引起,二者最终表现为惯性器件的输出异常。激光惯组是以激光陀螺为核心器件,激光陀螺相比于其他陀螺具有可靠性高、寿命长及长期精度稳定性好等优点,从使用方长期积累的维修数据发现,激光陀螺出现故障的几率比较小。另一方面,惯组内部各功能板上的电路主要是实现陀螺的抖动、稳频、稳流和信号检测功能,而电路中的元器件由于老化及环境影响出现故障的几率比较大,导致电路无法完成正常的控制功能,最终就会导致惯性器件输出异常。
由于惯组属于复杂机电系统,要建立其准确的数学模型或者物理模型十分困难;而且由于整个系统故障演化机理复杂,可能引起故障的因素很多,因此基于惯组模型的故障预测技术难以满足维修决策需求。为此,当前对于惯组故障预测技术的研究多是采用基于数据驱动的方法,通过分析陀螺仪的漂移数据进行剩余寿命预测。文献[1]提出采用EMD分解与多LSSVM集成预测方法、基于自适应EEMD和灰色极端学习机的多尺度混合预测模型等5种方法进行基于陀螺仪漂移数据的故障预测。文献[2]提出基于Wiener过程且同时考虑随机退化和不确定测量的退化建模方法,用于基于陀螺仪退化测量数据的剩余寿命预测。文献[3]提出将基于Copula函数的多退化变量剩余寿命预测方法用于基于陀螺仪漂移数据的剩余寿命联合分布。文献[4]采用漂移布朗运动对陀螺仪进行退化建模,针对陀螺仪性能参数样本容量小的实际情况,将改进Bayesian Bootstrap方法引入到陀螺仪退化模型参数估计中,有效地提高了预测精度。文献[5]首先利用基于线性漂移的布朗运动建模陀螺仪退化过程,然后构建状态空间模型表征不完整测量与实际退化状态的关系,并将估计的退化状态分布引入剩余寿命预测过程中,得到剩余寿命概率密度函数的参数化解析形式。这样,一旦获得新的监测值,即可更新未知参数与退化状态,相应地更新剩余寿命的分布,实现在线剩余寿命预测,减小了剩余寿命预测的不确定性。
但是由于激光陀螺的高可靠性,在实际应用中,很难得到激光陀螺从正常到故障全生命周期的监测数据,而采用加速疲劳的方法不仅成本高,获得的数据也不具有通用性。为此,本文针对激光陀螺周边控制电路的可靠性大大低于激光陀螺,而其稳定性又会对惯组可靠性产生很大影响的特点,提出了基于稳流电路退化过程建模的激光惯组剩余寿命预测方法,从而为激光惯组这类高可靠性系统的故障预测和剩余寿命预测技术的研究提供了新的思路。
1 稳流电路的功能
在现有技术条件下,零漂误差是决定激光惯组精度以及使用价值的重要因素。激光惯组的零点漂移(零偏)是指在输入角速度为0时,激光陀螺仪有不为0的频差输出,产生零漂的原因很多,其主要原因是朗缪尔流效应。
激光陀螺稳流电路的主要功能是调整电流,稳定气体在定向流动过程中由于指令流放电引起的误差。研究表明,在环形激光器的设计中,采用对称平衡的放电方式可以很好地消除朗缪尔流效应造成的误差。
稳流电路系统中的对称放电方式一般是指将环形激光放电管的中心连接到阴极管,然后放电管的两端分别与另外2根阳极管连通,形成2个相对的定向放电图形,使得对放电管的不同流动效应相互抵消或平衡,如图1所示。

图1 激光陀螺对称平衡放电示意图
为了达到消除零漂的目的,要求两路电流完全对称,但实际上是无法做到这一点的。并且随着时间的增长,系统老化和环境因素的影响会使这种不对称度增大,导致输出的电流差值越来越大,产生的零漂误差也随之增大。为此,我们考虑对稳流电路进行分析,找出能表征电路健康状态的参数及相应的失效阈值,作为激光惯组的一项健康指征,并通过对该健康指征衰变规律的分析,进行稳流电路剩余寿命的预测,进而对惯组剩余寿命进行预测。
2 稳流电路特性分析
从图2可以看出,单路稳流电路实际上是一个压控恒流源,其功能就是用电压控制电流的变化。稳流电路主要由基准电源VREF、输入控制电压Vi、运算放大器IC、场效应管M1(也可使用双极性晶体管)和基准电阻R组成[6]。

图2 单路稳流电路原理图
通常在稳流电路中,场效应管被设计为正常工作在恒流区。漏极输出电流Io的变化反映了场效应管漏极和源极之间导电沟道等效电阻RDS的变化。漏极电流如果是一个定值,增大反映了RDS的减小,而Io减小反映了RDS的增大,因此可将RDS作为被控对象。在恒流区可定义
式中,N为压阻系数,单位为VΩ。该系数的大小反映了VGS对RDS的控制能力,这样场效应管可以等效成一个受控的可变电阻。当VGS为一定值的时候,RDS为一定值,漏极电流Io也为一定值。
当Io上升时,有
Io↑⟹Vo↑⟹V32↓⟹VG↓⟹VGS↓⟹RDS↑⟹Io↓
当Io下降时,有
Io↓⟹Vo↓⟹V32↑⟹VG↑⟹VGS↑⟹RDS↓⟹Io↑
这样就保证了输出电流稳定在一定的水平,当电流稳定后,运算放大器的2、3输入脚电压相等,即
V2=V3
又Vo=V2
由于场效应管的栅极电流很小,可以忽略不计,则
则
令
则
电流相对稳定度可表示为
以上推论是在理想情况下得出的结论。在实际运行过程中,除了采样电阻的取值和基准电压的稳定性会对电路产生影响之外,运放和场效应管(或者晶体管)等元器件自身的变化也会对电路产生一定的影响。
根据以上分析可以看出,稳流电路相关元器件的退化将会导致电路稳流功能的退化,并最终以两路输出电流差值的形式表现出来。当两路电流差值大于设定的平衡精度时(这里设为5μA,即当两路输出电流差值大于5μA时,稳流电路处于故障模式),会导致陀螺增益不稳定,从而影响激光陀螺的输出。为此,我们考虑将稳流电路两路输出电流差值作为激光惯组的一项健康指征,当它超过一定的阈值时,就认为无法输出满足激光陀螺控制所需要的稳定电流,进而导致激光惯组输出异常。
3 稳流电路仿真数据处理和分析
根据前面对稳流电路系统特性的分析,我们用Simulink 软件对某典型稳流电路进行了建模,如图3所示,用基于该模型的仿真数据模拟稳流电路的实际输出数据,并将关键元器件的衰变曲线引入仿真系统,获得关键元器件衰变影响下的两路电流差值变化曲线。

图3 激光陀螺稳流电路仿真图
本文分别将取样电阻、运算放大器和场效应管等元器件的退化曲线引入仿真系统(各部件退化均为线性退化模型),得到仿真输出的电流差值曲线如图4~6所示。

图4 取样电阻退化后的电流差值曲线

图5 运算放大器退化后的电流差值曲线

图6 场效应管退化后的电流差值曲线
利用轮次检验法,对稳流电路仿真输出数据进行平稳性检验,发现3组原始数据序列都是非平稳的。为了更好地对输出的电流差值数据进行分析,找到其变化规律,本文用一次差分法对数据进行平稳化处理,如图7~9所示。一次差分法是一种简单的平稳化处理方法,它在平稳化数据的同时能最大限度地保留数据中的信息。

图7 第一组仿真数据差分后的平稳时间序列

图8 第二组仿真数据差分后的平稳时间序列

图9 第三组仿真数据差分后的平稳时间序列
对平稳化处理后的时间序列退化数据进行动态分析,求出序列的自相关函数和偏相关函数,如图10~12所示。从图中的拖尾截尾特性可以初步辩识稳流电路输出电流差值数据可以用ARMA模型进行拟合。

图10 第一组平稳时间序列自相关、偏相关函数

图11 第二组平稳时间序列自相关、偏相关函数

图12 第三组数据时间序列自相关、偏相关函数
表1~3分别为3组平稳时间序列DDS建模结果。从表中可以看出,拟合出来的3组模型中,ARMA(2,1)的AIC和FPE是最小的。因此,认为稳流电路输出电流差的模型为ARMA(2,1)。其模型结构为:
xt=φ1xt-1+φ2xt-2+at-θ1at-1
由表中φ1和φ2可知,其绝对值都小于1,说明模型是稳定的。

表1 第1组数据建模结果
第1组平稳时间序列建立的模型差分形式为:xt=0.4432xt-1+0.5453xt-2+at-0.9605at-1
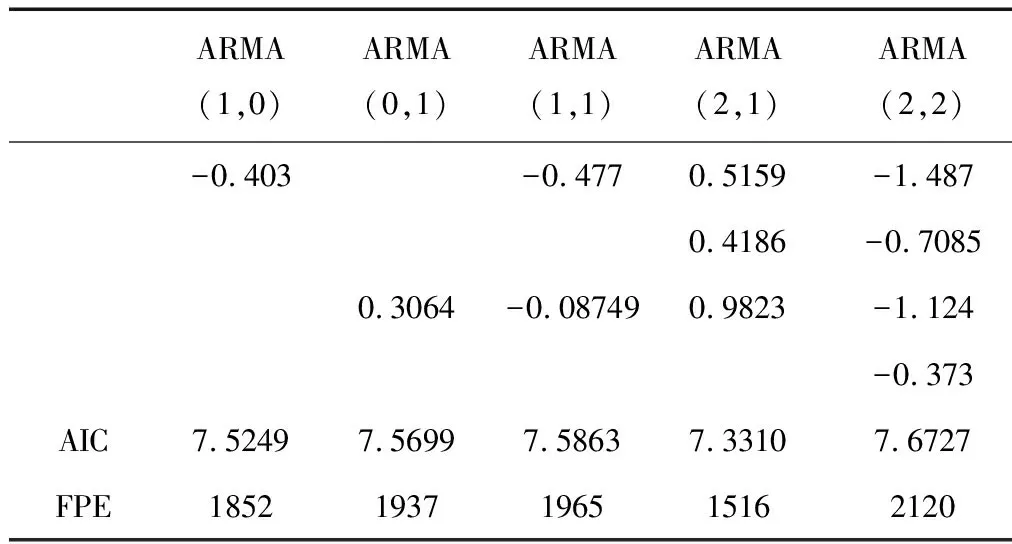
表2 第2组数据建模结果
第2组平稳时间序列建立的模型差分方程形式为:
xt=0.5149xt-1+0.4186xt-2+at-0.9823at-1

表3 第3组数据建模结果
第3组平稳时间序列建立的模型差分方程形式为:
xt=0.4233xt-1+0.5407xt-2+at-0.964at-1
ARMA(p,q)模型的建立是从模型辨识和参数估计开始的重复适应过程。在估计完参数、建立好初步模型之后,还需要进行假设性检验去检验所建立的模型是否合适。
通过对3组时间序列模型进行分析,得到相应的残差图,设定显著性水平a=0.05,通过LB检验得到相应的P值。当P值大于0.05时,接收原假设;小于0.05时,拒绝原假设。由表4可以看出,3组数据的P值均大于0.05,可知3组残差均为白噪声,这说明根据3组数据建立的模型具有良好的适应性。

表4 残差检验统计结果
4 激光惯组剩余使用寿命预测
剩余使用寿命预测就是在当前时刻t1,根据系统当前的年龄、工作条件和状态监测信息预测健康指征未来的发展趋势直到健康指征HI首次到达失效阈值,此时即为系统失效时间(TTF,Time-to-failure)。t1时刻RUL预测值可表示为:
(1)
其中,TTF1*为t1时刻系统失效时间的预测期望。

根据前面拟合的ARMA模型:
xt=φ1xt-1+φ2xt-2+at-θ1at-1



以此类推:x2=φ1x1+φ2x0-θ1a1+a2


以此类推:xt=φ1xt-1+φ2xt-2+at-θ1at-1


xt+1=φ1xt+φ2xt-1+at+1-θ1at;



以此类推:
xt+2=φ1xt+1+φ2xt+at+2-θ1at+1
E(xt+3)=φ1E(xt+2)+φ2E(xt+1)
E(xt+l)=φ1E(xt+l-1)+φ2E(xt+l-2)
E(xt+l)就是xt+l在t+l时刻的预测值。
根据3个序列模型x0,x1,…,xt的仿真数据,可以分别对稳流电路输出电流差t时刻之后的数据进行预测。设在任意一组预测数据中,当两路电流的差值达到5μA时,认为稳流电路达到其寿命阈值。取3个序列中最先达到失效阈值的时刻t+l,根据公式(1)计算得到系统的剩余使用寿命。表5为3组仿真数据分别提前l期进行预测得到的剩余使用寿命期望和电路仿真得到的两路电流差值的对比数据,根据预测值和仿真值的比较,能够看出所建立的模型能够较好地预测出系统的剩余使用寿命。

表5 提前l期的剩余使用寿命预测
5 结论
本文从激光惯组误差产生机理出发,提出了一种基于稳流电路退化过程建模的激光惯组剩余寿命预测方法,该方法以稳流控制电路仿真衰变数据为依据,用ARMA模型对表征电路健康状态的数据进行拟合,进而对激光惯组剩余寿命进行预测,仿真试验证明了该方法的有效性。本方法为激光惯组这类高可靠性系统的故障预测和剩余寿命预测技术的研究提供了新的思路。
